Engineering Physics: Unit IV: Basic Quantum Mechanics
Solved Problems of Basic Quantum Mechanics
Engineering Physics
SOLVED PROBLEMS of Basic Quantum Mechanics : Engineering Physics: Basic Quantum Mechanics
ANNA UNIVERSITY SOLVED PROBLEM Problem 6.1 An electron is accelerated by a potential difference of 150 V. What is the wavelength of that electron wave? Given data Accelerating voltage applied to the electron V = 150 V Solution We know that the de - Broglie wavelength Substituting the given values, we have Problem 6.2 Calculate de - Broglie wavelength of an electron of energy 100 eV Given data Energy of electron E = 100 eV E = 100 × 1.6 × 10-19 joule (⸪ 1eV = 1.6 × 10-19 J) Mass of the electron m = 9.1 × 10-31 kg Planck's constant h = 6.625 × 10-34 Js Solution We know that λ = Substituting the given values, we have de - Broglie's wavelength λ = 1.235 × 10-10 metre Note: At the time de - Broglie proposed his hypothesis, there was no experimental evidence to show that the particles of matter like electrons, protons, neutrons etc., have wave properties. However, the wave nature of atomic particles was experimentally verified by the American scientists Davisson and Germer in 1927 and by G.P. Thomson in 1928 and thus the truth of de Broglie concept was established. In quantum mechanics it is postulated that there exists a function determined by the physical situation. The function is called wave function. It is also postulated to contain all possible information about the system. Hence, it is also called as state function. The wave function may vary with respect to both the position coordinates of the physical system and the time. It is then called the total wave function, and is represented by the capital form of the greek letter Ψ (pronounced as psi). If the wave function has variation only with position (i.e., space) and not with time, it is represented by the lower case greek letter Ψ. The total wave function can be represented by the equation, where, A is a constant, and w is the angular frequency of the wave. Separating the space and time dependent parts, Ψ can be expressed as, In the above equation, separating out the time dependent part, we can represent the rest as a space dependent wave function. Ψ is time independent wave function. The total wave function is now written as, The wave function in quantum mechanics accounts for the wave-like properties of a particle. It is obtained by solving a fundamental equation called Schrondinger equation. To solve the schrodinger equation it requires the knowledge of, (i) potential energy of the particle, (ii) initial conditions, and (iii) boundary conditions. Problem 6.3 Find the energy of an electron moving in one-dimension in an infinitely high potential box of width 0.1 nm. Given data a = 0.1 nm = 0.1 × 10-9 m Solution We know that energy of an electron where n = 1, 2, 3, ... The lowest energy of the particle is obtained for n = 1. Problem 6.4 In a Compton scattering experiment, the incident photons have a wavelength of 3 × 10-10m. Calculate the wavelength of scattered photons if they are viewed at an angle of 60° to the direction of incidence. Given data Wavelength of incident X -rays λ = 3 × 10-10m, Angle of scattering θ = 60° h = 6.625 × 10-34 Js m0 = 9.1 × 10-31 c = 3 × 108 ms-1 Solution: We know that Substituting the given values, we have Problem 6.5 X-rays of 1.0 Å are scattered from a carbon block. Find the wavelength of the scattered beam in a direction making 90° with the incident beam. How much kinetic energy is imparted to the recoiling electron? Given data Wavelength of incident X - rays λ = 1 Å = 1 × 10-10m Angle of scattering θ = 90° h = 6.625 × 10-34 Js. c = 3.0 × 108 ms-1 1 eV = 1.6 × 10-19 joule. Solution The change in wavelength is given by Δλ = 0.0242 × 10-10 = 0.0242 Å Now λʹ = λ + Δλ = 1.0 + 0.0242 = 1.0242 Å = 1.0242 × 10-10 m Energy of incident X-ray photon = hc/ λ Energy of scattered X-ray photon = hc/ λʹ ⸫ Energy imparted to the recoiling electron Problem 6.6 A neutron of mass 1.675 × 10-27 kg is moving with a kinetic energy 10 keV. Calculate the De-Broglie wavelength associated with it. Given data Mass of the neutron = 1.675 × 10-27 kg Kinetic energy = 10 keV = 10 × 103 eV = 10 × 103 × 1.6 × 10–19 J Planck's constant h = 6.625 × 10-34 Js Solution: Substituting the given values, we have Problem 6.7 An electron at rest is accelerated through a potential of 5000 V. Calculate de - Broglie wavelength of matter wave associated with it. Given data Accelerating potential (V) = 5000 V Solution Substituting the given values, we have Problem 6.8 Calculate de - Broglie wavelength associated with a proton moving with a velocity equal to one-thirtieth of the velocity of light. Given data Velocity of the proton v = 1/30 × velocity of light = 1/30 × 3 × 108 ms-1 = 1 × 107ms-1 Mass of the proton m = 1.67 × 10-27 kg Planck's constant h = 6.625 ×10-34 Js Solution We know that de - Broglie wavelength λ = h/mv Substituting the given values, we have Problem 6.9 If the momentum of two particles are in the ratio 1 : 0.25, compare their de - Broglie wave lengths. de - Broglie wavelengths associated with two particles of momentum in the ratio 1 : 0.25 are λ1 and λ2 de - Broglie wavelengths are in the ratio Problem 6.10 Calculate the de - Broglie's wave length of an electron having a velocity of 106 m/sec. Given data Velocity of the electron v = 106 ms-1 Mass of the electron m = 9.1 × 10-31 kg Planck's constant h = 6.625 × 10-34 Js Solution We know that de - Broglie's wavelength λ = h / mv Substituting the given values, we have Problem 6.11 Calculate the de - Broglie's wavelength associated with an electron which travels with a velocity 500 km s-1. Given data Velocity of the electron v = 500 km/sec = 500 × 103 ms-1 Planck's constant h = 6.625 × 10–34 Js Mass of the electron m = 9.1 × 10-31 kg Solution We know that de-Broglie's wavelength associated with electrons Substituting the given values, we have Problem 6.12 Calculate the minimum energy an electron can possess in an infinitely deep potential well of width 4 nm. Given data Width of potential well a = 4 nm = 4 × 10-9 m For minimum energy, n = 1 Mass of the electron m = 9.1 × 10-31 kg Planck's constant h = 6.625 × 10-34 Js Solution: Substituting the given values, we have Problem 6.13 An electron is trapped in a one-dimensional box of| length 0.1 nm. Calculate the energy required to excite the electron from its ground state to the fifth excited state. Given data Length of the one dimensional box a = 0.1 nm = 0.1 × 10-9 m For ground state n = 1 For 5th excited state, n = 6 Solution For 5th excited state, n = 6 The energy required to excite the electron from its ground state to the fifth excited state is ΔE = E6 – E1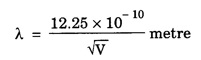

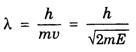
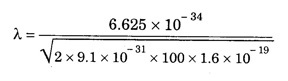
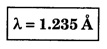
Concept of Wave Function



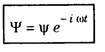
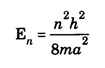

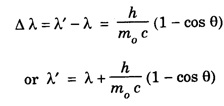

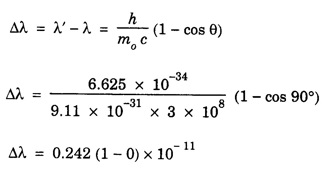
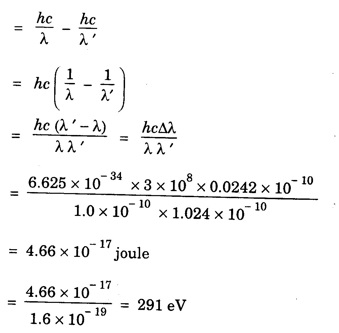
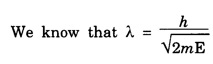

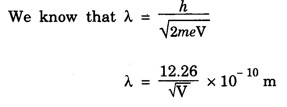
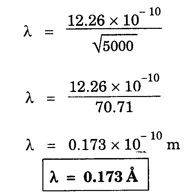
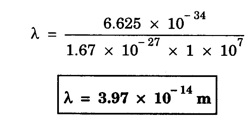
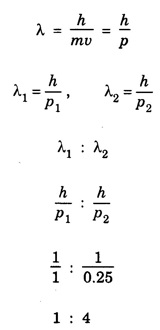
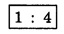

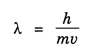
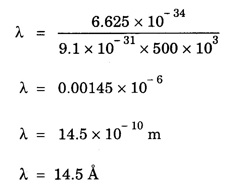
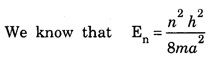
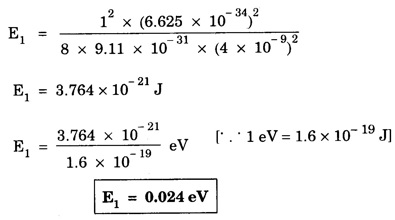
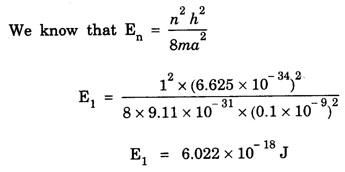
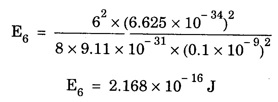

Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Engineering Physics - Solved Problems of Basic Quantum Mechanics
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
