Strength of Materials: Unit IV: Deflection of Beams
SOLVED PROBLEMS
Deflection of Beams - Strength of Materials
Deflection of Beams : Deflection of Beams - Strength of Materials
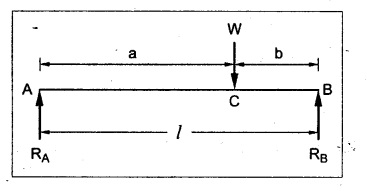
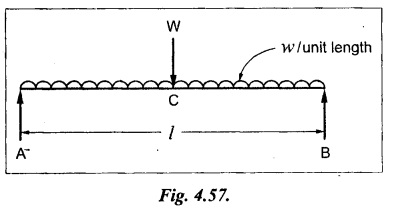
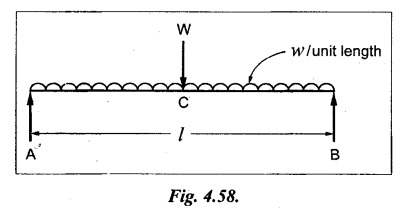
SOLVED PROBLEMS Example 4.14 A beam of length 'l' freely supported at the ends is loaded with a point load 'W' as shown in Fig.4.56. Assume Young's modulus 'E' and moment of inertia 'I' is constant. Find the deflection under the load. Given: To find: Deflection (yc) Solution: Taking moment about B, Let yc = Deflection under load. Equating strain energy and work done Result: The Maxwell's reciprocal theorem state that, "The work done by the first system of loads due to displacements caused by a second system of loads equals the work done by the second system of loads due to displacements caused by the first system of loads." Proof: Let point forces Pi, i = 1,2, ..., n act on an elastic body constrained in a space. Then the strain energy due to this force system is given by, For finding the strain energy of the body under the combined action of both the force systems A and B, let us assume that the principle of superposition holds good so that the order of application of the loading system does not change the final result. Now, applying force system A to the body the strain energy UA is given by, Further, apply the force system B to the body, the force system A remains constant during application of force system B, the strain energy UA,B is given by Now, the increase in strain energy UB is given by, Now, when the body is reloaded in reverse, the strain energy According to the principle of superposition, we have Hence the theorem is proved. Example 4.15 A simply supported beam of span I is carrying a concentrated W at the centre, and a uniformly distributed load of intensity of w per unit length. Show that Maxwell's reciprocal theorem holds good at the centre of the beam. Given: To find: Prove Maxwell's theorem. Solution: Let the load P is applied first and then udl w. Deflection due to load w at the centre of the beam is given by Hence, work done by P due to w is given by, Now, deflection at a distance x from the left end due to P is given by, Work done by w per unit length due to P, Therefore, equating the equation (1) and (2), Hence, the Maxwell's theorem is proved.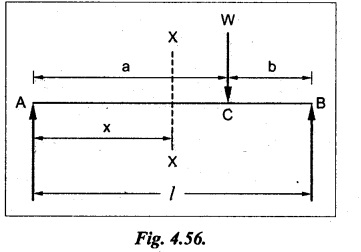
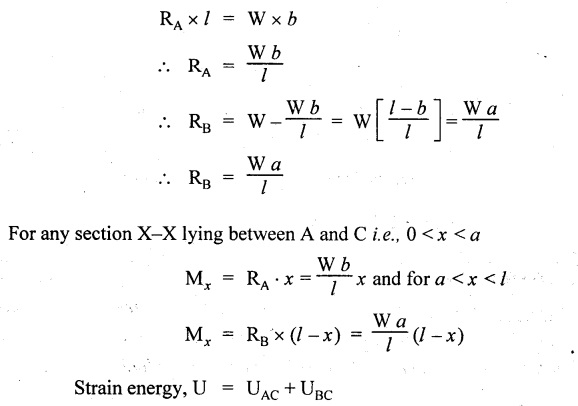
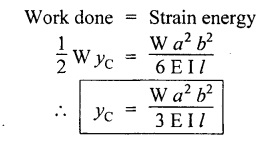
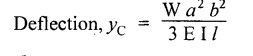
MAXWELL'S RECIPROCAL THEOREM
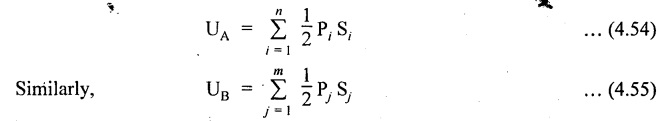
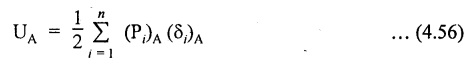

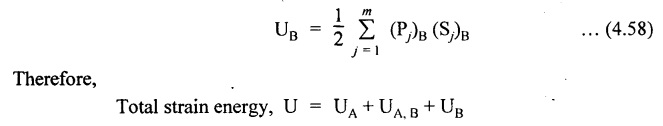
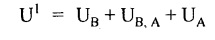
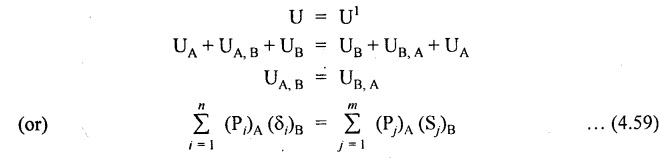
PROBLEM SOLVED ON MAXWELL'S RECIPROCAL THEOREM
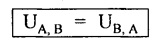
Strength of Materials: Unit IV: Deflection of Beams : Tag: : Deflection of Beams - Strength of Materials - SOLVED PROBLEMS
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
