Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
Solved Examples Problems: Resultant Force
Miscellaneous Solved Examples: Equilibrium of Rigid Bodies - Engineering Mechanics
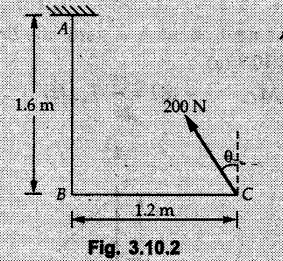
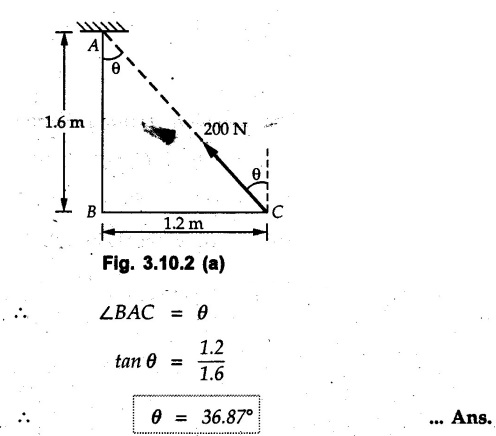
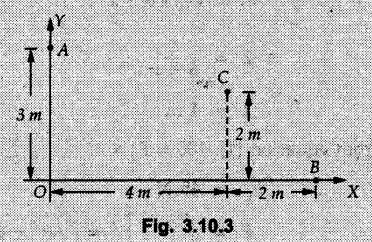
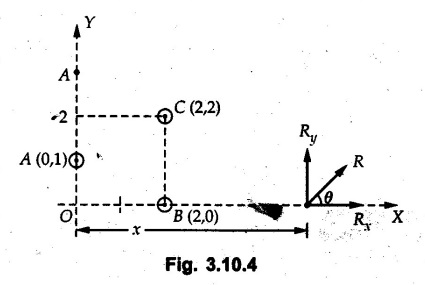
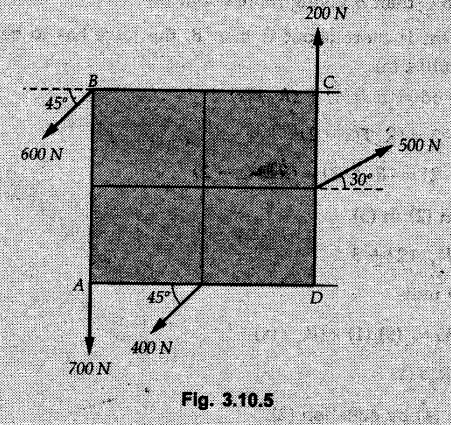
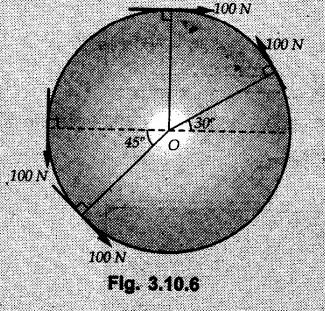
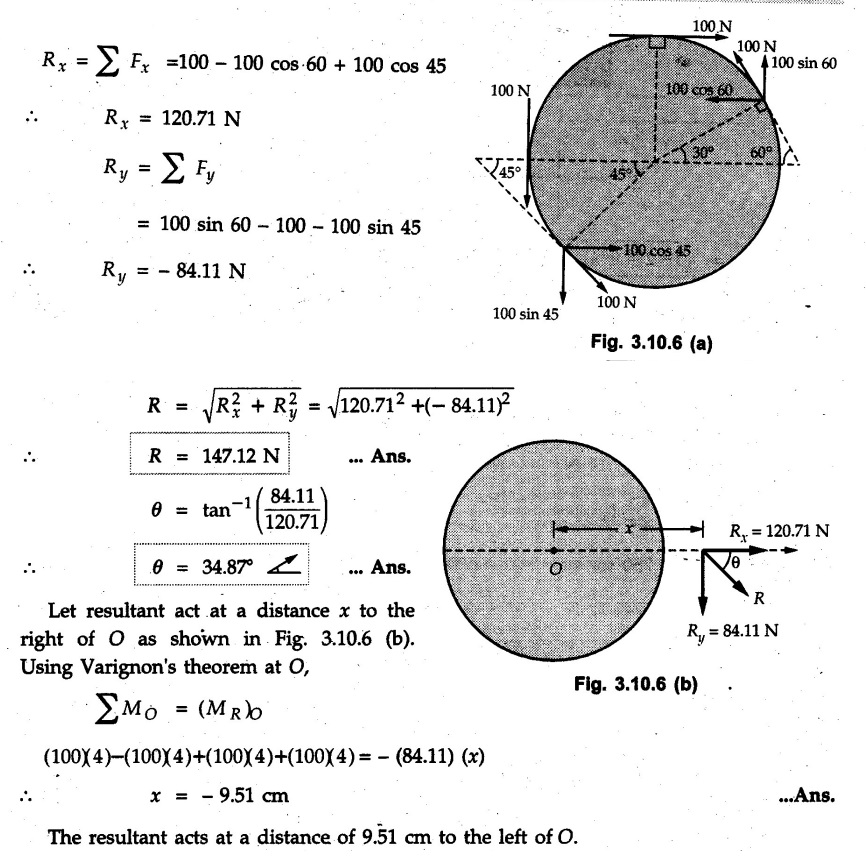
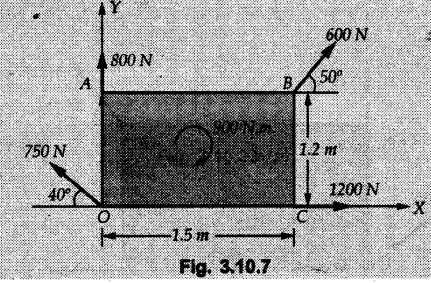
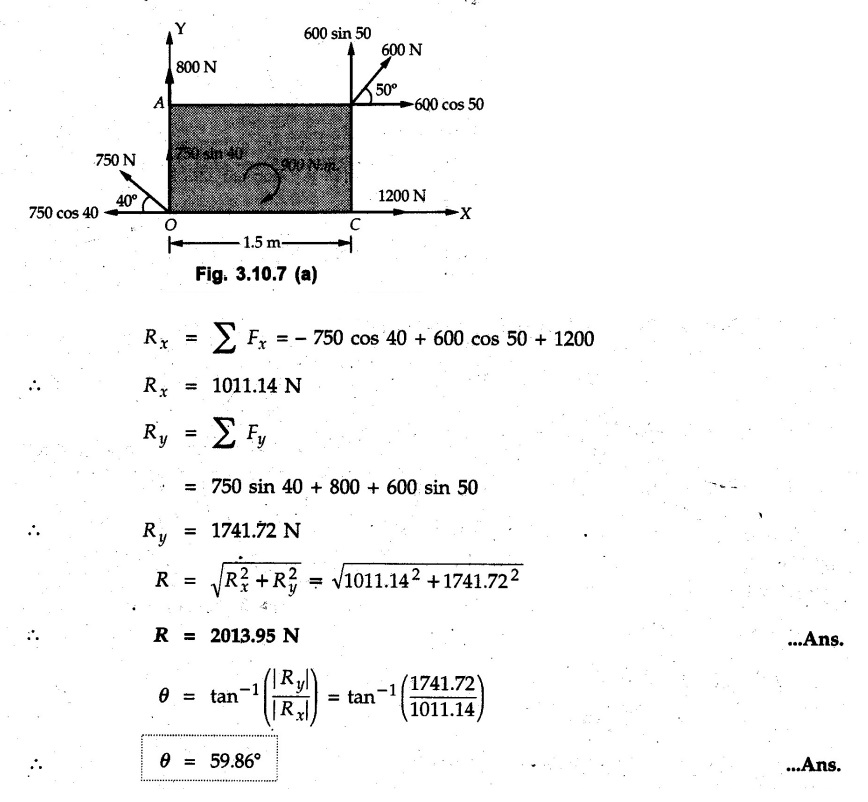
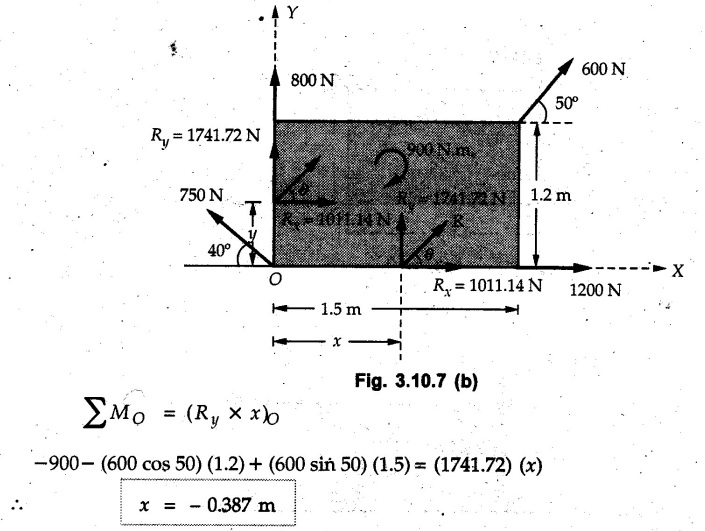
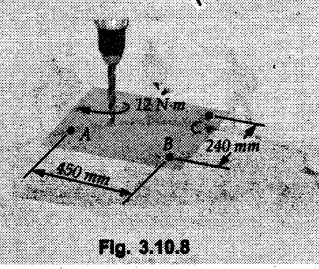
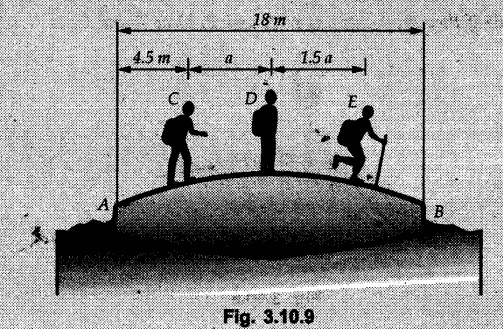
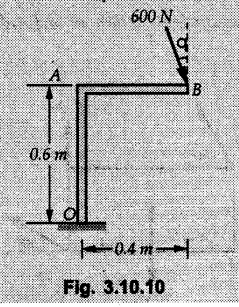
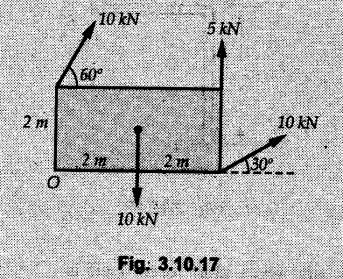
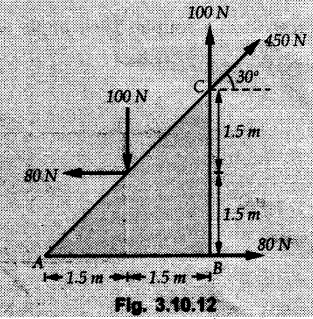
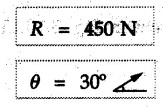
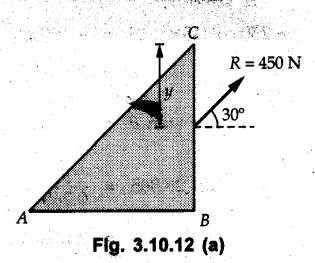
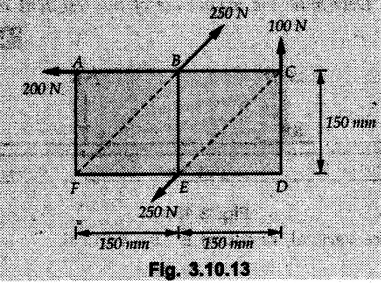
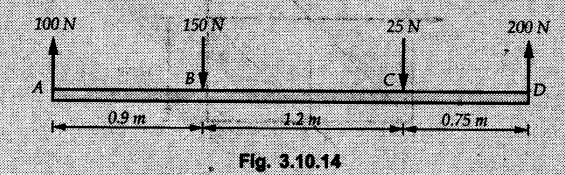
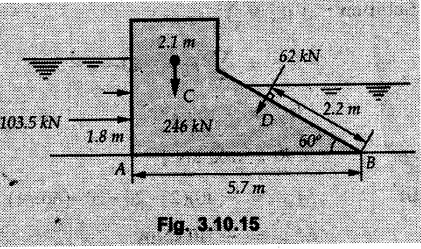
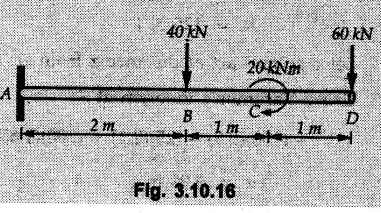
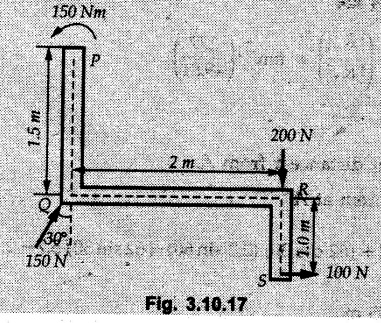
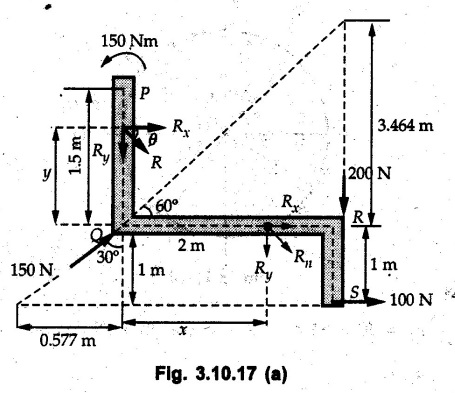
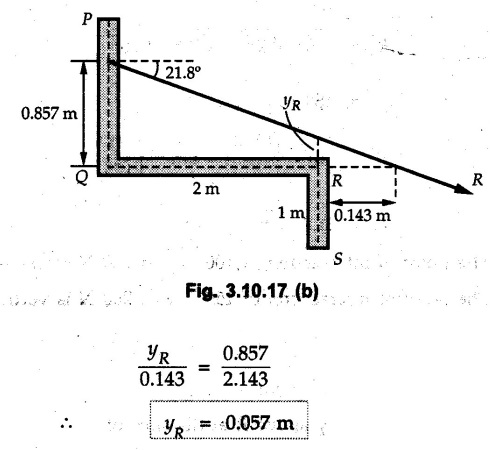
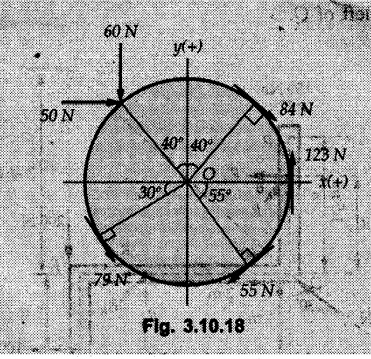
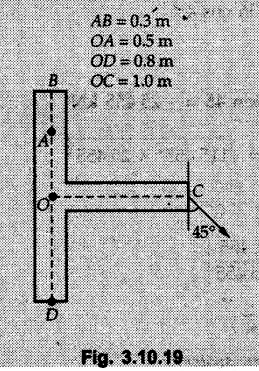
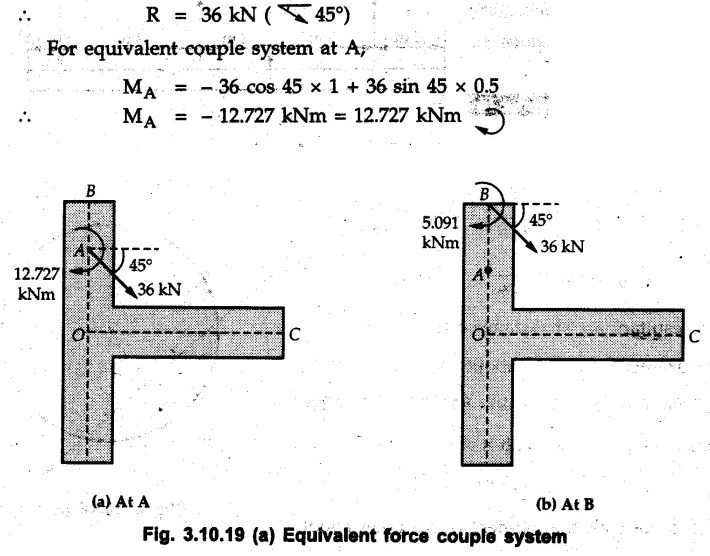
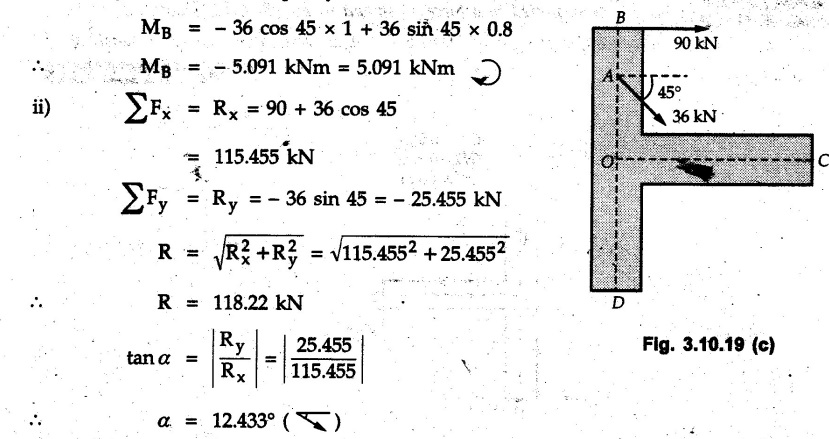
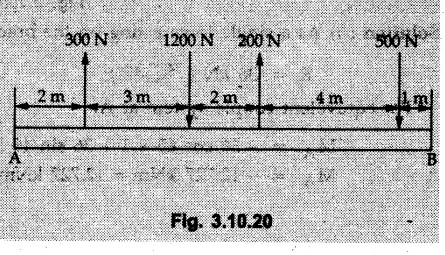
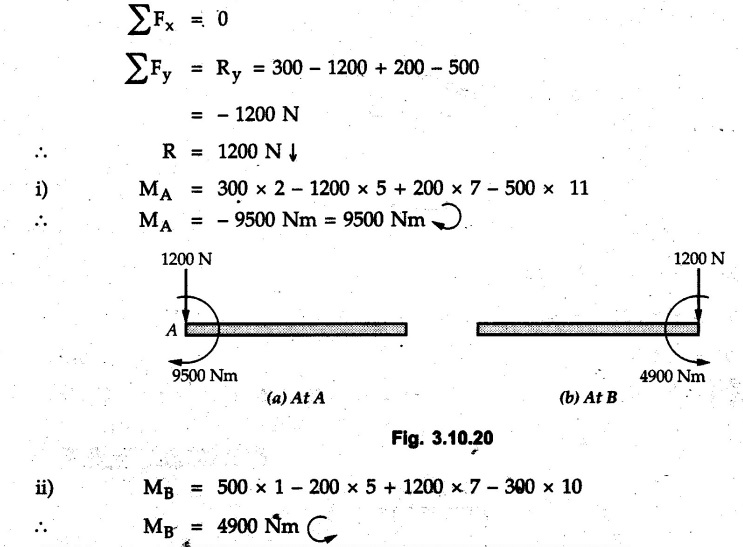
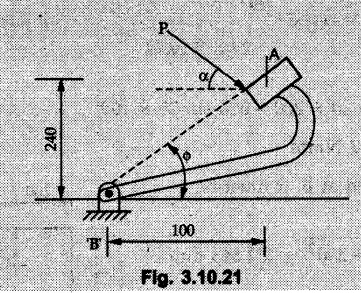
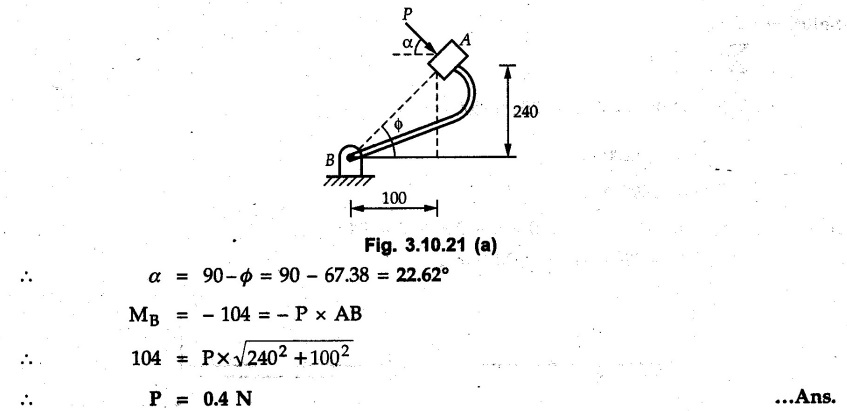
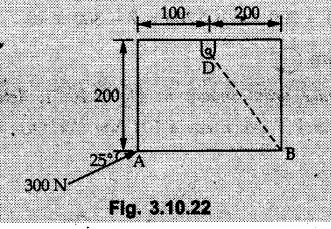
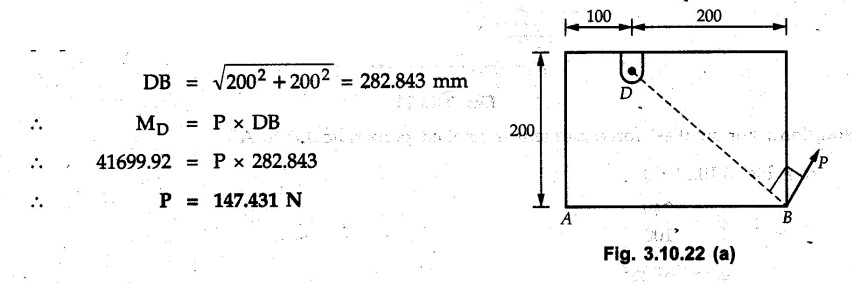
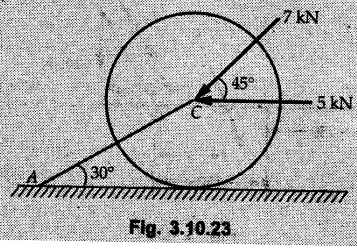
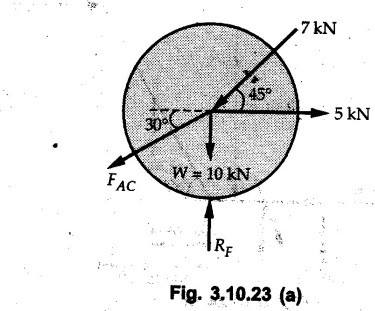
Miscellaneous Solved Examples Example 3.10.1 Determine the magnitude and direction of resultant with reference to point A for the force system as shown in Fig. 3.10.1 if side of equilateral triangles is 1 m. Solution: As the resultant force is zero, the resultant can be a moment which will be same about any point in the plane. Taking moment about B, This moment can be anywhere in the plane. Example 3.10.2 The lever ABC fixed at A shown in Fig. 3.10.2 is subjected to a 200 N force at C at θ = 30°. Find the moment of this force about A. Also, find the value of for which the moment about A is zero. Solution : Resolve the force into two components : i) Horizontal component 200 sin 30 towards left ii) Vertical component 200 cos 30 upward. ⸫ The moment of this force about A is For moment of force to be zero about A, its line of action must pass through A as shown in Fig. 3.10.2 (a) Example 3.10.3 Fig. 3.10.3 shows points A, B and C lying in X-Y plane. in X-Y plane. The moment of a certain force F acting in X-Y plane is 180 Nm clockwise about the origin and 90 Nm anticlockwise about point B. If its moment about A is zero determine the magnitude, direction of force F and moment of force about point C. Solution: • As moment of force is clockwise about O and anticlockwise about B, the line of action of force has to be between O and B. • As moment about A is zero, the line of action has to pass through A as shown in Fig. 3.10.3 (a). Example 3.10.4 The moments of a given plane system of forces about three points (0, 1), (2, 0) and (2, 2) are +36, + 3 and + 21 units respectively. Find the resultant force. Solution : The three points A (0, 1), B (2, 0) and C (2, 2) are as shown in Fig. 3.10.4. • As all the moments are anticlockwise, the line of action of force should not intersect the three lines AB, BC and AC. R cannot be in IIIrd or IVth quadrants as it will give clockwise moment. • If R is in IInd quadrant it will be closer to C than B giving more about B. • As given moment is more about C than B, the force has to be in Ist quadrant as shown in Fig. 3.10.4 (a). Dividing equation (4) by equation (2), Example 3.10.5 Find the resultant in magnitude and direction for the force system shown in Fig. 3.10.5. Each square has side 0.25 m. Also determine the position of the resultant on the line AD. Solution : Let the resultant act at a distance x from A on the line AD as shown in Fig. 3.10.5 (b). Using Varignon's theorem at A. Example 3.10.6 Four forces act tangentially to a 8 cm diameter circle as shown in Fio 3.10.6. What will be magnitude and location of resultant with respect to 'O'. Solution : Example 3.10.7 Find the resultant of the force system acting on a body OABC as shown in Fig. 3.10.7. Also find the points where the resultant will cut the X and Y axis. Solution : The X-intercept of the resultant can be obtained by plotting the resultant on X-axis at a distance x from O as shown in Fig. 3.10.7 (b) and using Varignon's theorem at O. i.e., resultant acts at a distance of 0.387 m to the left of O. The Y-intercept can be obtained by plotting resultant on Y-axis at distance 'y' as shown in Fig. 3.10.7 (b). Using Varignon's theorem at O, i.e., resultant at a distance of 0.666 m above O. Example 3.10.8 A piece of plywood in which several holes are being drilled successively has been secured to a workbench by means of two nails. Knowing that the drill exerts a 12 Nm couple on the piece of plywood, determine the magnitude of the resulting forces applied to the nails if they are located a) at A and B, b) at B and C, c) at A and C. Solution: Couple consists of two equal and opposite forces separated by some distance. Let magnitudes of the two forces exerted on the nails in each case be F. Given moment M = 12 Nm Example 3.10.9 Three hikers are shown crossing a footbridge. Knowing that the weights of the hikers at points C, D and E are 200 N, 175 N and 135 N, respectively, determine the horizontal distance from A to the line of action of the resultant of the three weights when a = 3.3 m. Solution: The resultant of the three forces is R = 200 + 175 + 135↓ Let the resultant act at distance 'x' from point A. Using Varignon's theorem at A, Example 3.10.10 A 600 N focre is applied at an angle θ = 20°. Determine the equivalent force couple system at point A and O. For what value of the results at point A and O should be identical. Refer Fig 3.10.10. Solution: As there is only one force, that force itself is the resultant force. i.e. R = 600 N. The equivalent force couple system at point O is shown in Fig. 3.10.10 (b). The equivalent force couple system at point A is shown in Fig. 3.10.10 (c). Results at A and O will be identical if MA = MO Hence results are identical if the given force is vertical. Example 3.10.11 Determine the equivalent action as defined by a single force for the force system shown in Fig. 3.10.11. Solution: As d is positive, resultant produces anticlockwise moment about O. The resultant is as shown in Fig. 3.10.11 (a). Example 3.10.12 Replace the force system acting on the triangular plate, ABC by a single force. Give the point of intersection of the line of action of this force with the vertical edge BC of the plate. Refer Fig. 3.10.12. Solution: The two 80 N and the two 100 N forces form couples. ⸫ Resultant force is Let the resultant cut at a distance y from C as shown in Fig. 3.10.12 (a). Using Varignon's theorem at C, (80) (3) + (100) (1.5) – (80) (1.5) = (450 cos 30) y ⸫ y = 0.693 m The resultant force acts at a distance of 0.693 m below C on the vertical edge BC. Example 3.10.13 A 150 × 300 mm plate is subjected to four loads. Find the resultant of the four forces and the two points at which the line of action of the resultant intersects the edge of the plate. Refer Fig. 3.10.13. Solution : The two 250 N forces form a couple. Their angle with horizontal is 45°. Let the resultant act at a distance x from C as shown in Fig. 3.10.13 (a). Using Varignon's theorem at C, - 250 cos 45 × 0.15 = 100 x ⸫ x = 0.265 m The line of action of resultant intersects AC at a distance of 0.265 m to the left of C and intersects CD at a distance of 0.1326 m below C. Example 3.10.14 Four parallel forces of magnitudes 100 N, 150 N, 25 N and 200 N are shown in Fig. 3.10.14. Determine the magnitude of the resultant and also the distance of the resultant form point A. Solution: As all forces are vertical, resultant is also vertical. Rx = 0 Example 3.10.15 Determine the resultant of the three forces acting on the dam shown in Fig. 3.10.15 and locate its intersection with the base AB. For a good design, this intersection should occur within the middle third of the base. Comment whether it is a good design or not. Solution : The middle one third of base is from 5.7/3 = 1.9 m to 2/3 (5.7) = 3.8 m. As x = 1.7507 m, it does not lie in the middle one third. Hence it is not good design. Example 3.10.16 Fig. 3.10.16 shows two vertical forces and a couple of magnitude 20 kNm, acting on a horizontal rod, which is fixed at A. a) Determine the resultant of the system b) Reduce to force - couple system at A. Solution: Example 3.10.17 A body is acted upon by a system of forces and a couple as shown in Fig. 3.7.27. Determine the resultant of the system of forces. Also locate the points of intersection of the system of forces. Also locate the points of intersection of the resultant with the arm PQ, QR and RS. Solution: The point of intersection of 100 N and 200 N forces is the point S. The point of intersection of 150 N and 200 N is vertically above R at distance of 2 tan 60 = 3.464 m The point of intersection of 150 N and 100 N forces is 1 m below and 1 tan 30 = 0.577 m to the left of Q. The points of intersections of these forces are shown in Fig. 3.10.17 (a). Let the resultant act at distance y on the arm PQ as shown in Fig. 3.10.17 (a). Using Varignon's theorem at Q, 150 (200) (2) + (100) (1) = - (175) y To find position on arm QR, plot resultant at distance x from Q on QR as shown in Fig. 3.10.17 (a). Using Varignon's theorem at Q, 150 (200) (2) + (100) (1) = (70) (x) ⸫ the point is 0.143 m to the right of R. The resultant is shown in Fig. 3.10.17 (b). It will cut RS above R. By similarity of triangles, Example 3.10.18 Find the resultant of the force system shown in Fig. 3.10.18. Radius = 2.5 Solution : As d is positive, the moment of resultant about O is anticlockwise. The resultant is shown in Fig. 3.10.18 (a). Example 3.10.19 A bracket is subjected to a force as shown in Fig. 3.10.19. Determine : (i) an equivalent force couple system at A and B (ii) an equivalent system consisting of 90 KN force at A. Solution: i) As a single force acting on the bracket, that is only the resultant. For equivalent force couple system at B, Example 3.10.20 Reduce the given system of forces acting on the beam AB in Fig. 3.10.20 to (i) an equivalent force couple system at A (ii) an equivalent force couple system at B. Solution : Example 3.10.21 For the brake pedal shown in Fig. 3.10.21, determine the magnitude and direction of the smallest force P which has a 104 Nm clockwise moment about B. Solution: For smallest force moment is applied perpendicular to AB. From Fig. 3.10.21 (a) Tan ϕ = 240/100 ⸫ ϕ = 67.38° Example 3.10.22 A 300 N force is applied at A as shown in Fig. 3.10.22. Determine : 1) The moment of force abut D, 2) The smallest force applied at B, which creates same moment. Solution : i). MD = 300 cos 25 × 200 - 300 sin 25 × 100 ⸫ MD = 41699.92 Nmm ii) For smallest force applied at B, it must be perpendicular to DB. Example 3.10.23 A roller of weight 10 kN rests on a smooth horizontal floor and is connected to the floor by the bar AC as shown in Fig. 3.10.23 (a). Determine the force in the bar AC and reaction from floor, if the roller is subjected to a horizontal force of 5 kN and an inclined force of 7 kN as shown in the figure. Solution : Applying equilibrium conditions, Example 3.10.24 The system of forces acting on a bell crank is shown in Fig. 3.10.24. Determine the magnitude, direction and the point of application of the resultant. Solution : Applying Varignon's theorem at point O,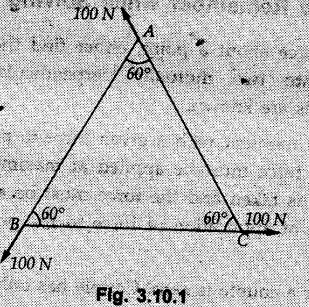
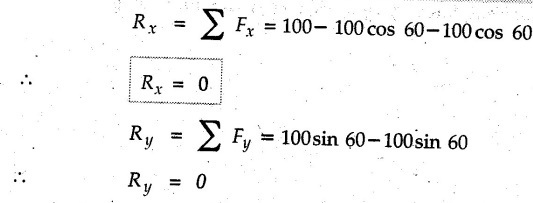















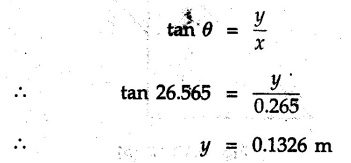



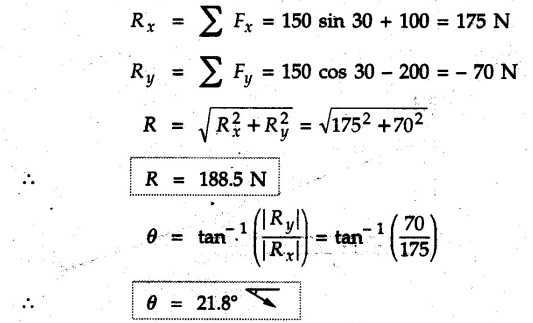
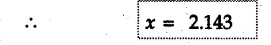




Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : - Solved Examples Problems: Resultant Force
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
