Engineering Mechanics: Unit V: Dynamics of Particles
Solved Example & Practice Problems: Projectile Motion
Solved Example Problems, Examples for Practice: Projectile Motion - Dynamics of Particles - Engineering Mechanics
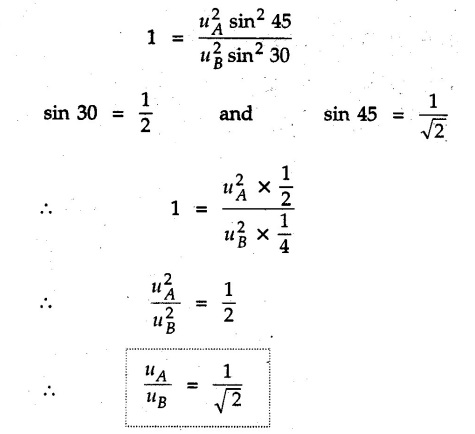
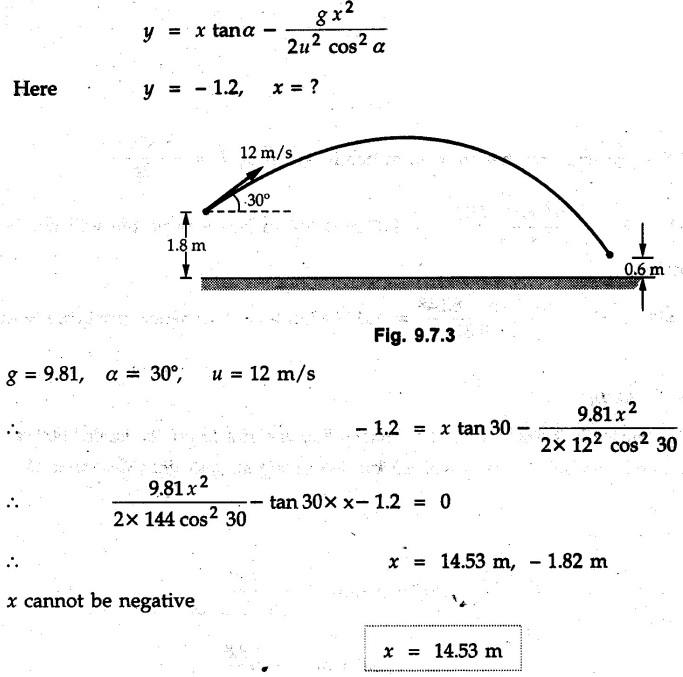
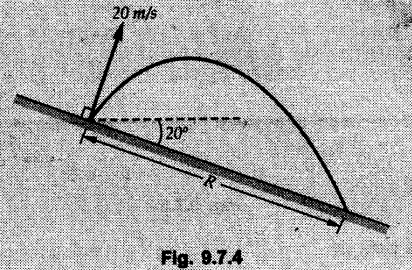
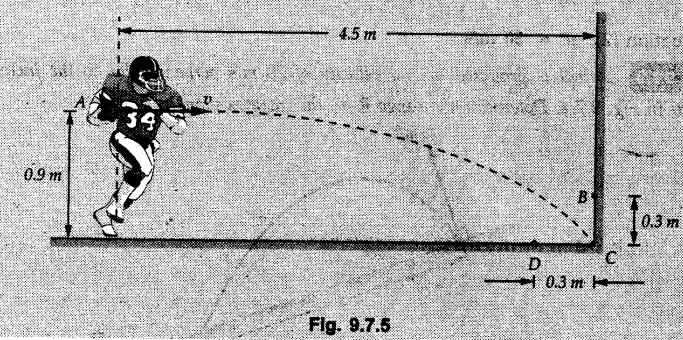
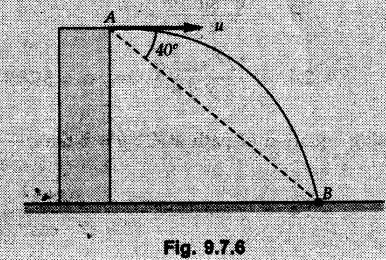
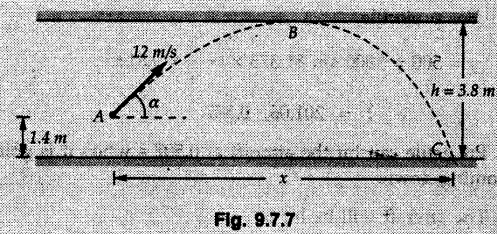
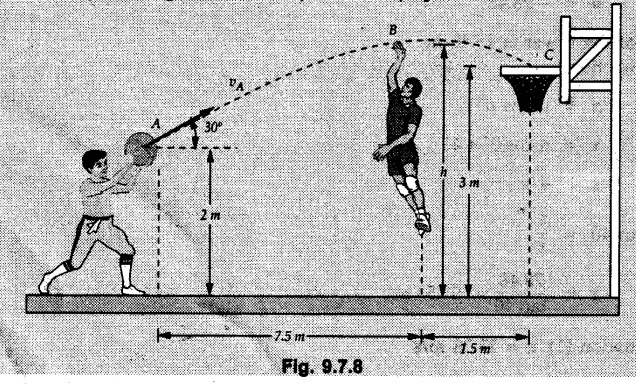
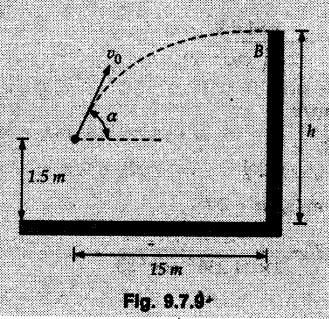
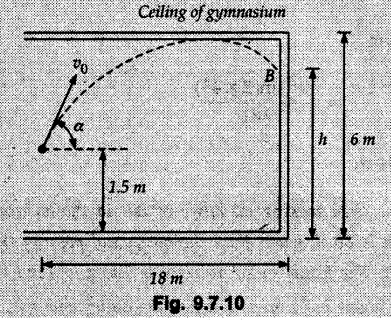
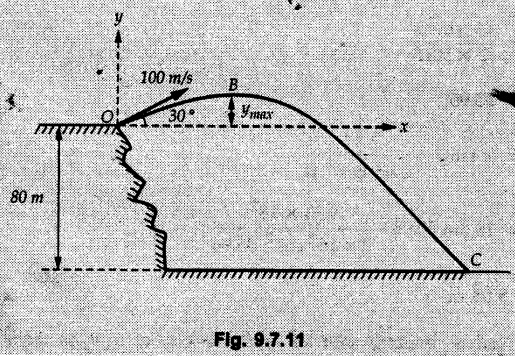
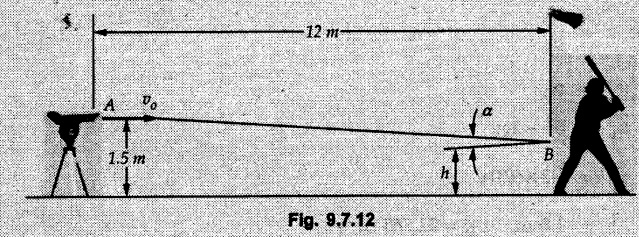
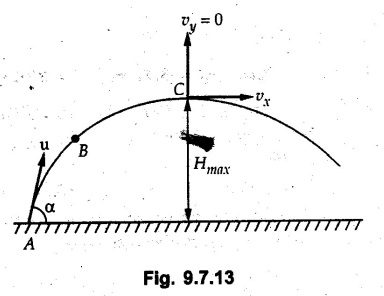
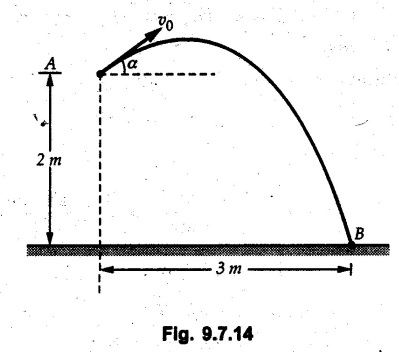
Projectile Motion Solved Examples for Understanding Example 9.7.1 Two stones A and B are projected from the same point at inclinations of 45° and 30° respectively to the horizontal. Find the ratio of the velocities of projection of A and B if the maximum height reached by them is the same. Solution: The maximum height reached by a projectile is given by Dividing equation (1) by equation (2), Example 9.7.2 From top of a 60 m tower, a bullet is fired at an angle of 60° with the horizontal, with a velocity of 120 m/s. Calculate the maximum height attained by the bullet and the time of its interval, when it strikes the ground. Solution: The maximum height above the point of projection is given by Taking starting point of motion as origin, the displacement in y-direction when bullet strikes the ground is - 60 m. Example 9.7.3 A particle is projected with an initial velocity of 60 m/s, at an angle of 75° with the horizontal. Determine a) The maximum height attained by the particle b) Horizontal range of particle c) Time taken by the particle to reach highest point d) Time of flight Solution : Example 9.7.4 A bomb is dropped from an aeroplane flying at a speed of 800 km/h at a height of 1500 m above the level ground. Find the horizontal distance covered by the bomb after its release. Also find the time required for the bomb to hit the target and the velocity with which the bomb hits the target. Solution: For the bomb, ux = 800 km/h = 222.22 m/s; uy = 0 ax = 0; ay = -9.81 m/s2 Taking starting point of motion of bomb as origin at the final point, Sy = -1500 m. Let t = Time of flight. Example 9.7.5 Horizontal distance of a target to be hit by a projectile is 8 km. Projectile leaves the cannon with a velocity of 550 m/s. What must be angle of elevation of the cannon? If the projectile has to clear a 700 m high hill midway between target and cannon, what should be the angle of elevation of cannon? Solution: Using equation of path At midway, the projectile reaches maximum height given by Example 9.7.6 A projectile is fired with initial velocity 240 m/s at a target 'B' located 600 m above the gun and a horizontal distance of 3.6 km. Neglecting air resistance, determine the firing angles. Solution: Equation of path Example 9.7.7 A cricket ball thrown from a height of 1.8 above ground level at an angle of 30° with the horizontal with a velocity of 12 m/s is caught by a fielder at a height of 0.6 m above the ground. Determine the distance between the two players. Solution: The equation of path is, Example 9.7.8 A projectile is launched from a gun. After 3.783 seconds, the velocity of the projectile is observed to make an angle of 30° with the horizontal and at 4.79 seconds it reaches its maximum height. Calculate the initial velocity and angle of projection. Solution: Example 9.7.9 A ball is projected with a velocity of 20 m/s perpendicular to the incline as shown in Fig. 9.7.4. Determine the range R on the inclined plane. Solution: Choosing starting point as the origin, the co-ordinates of the final point will be x = R cos 20 and y = -R sin 20. The displacements in x and y-directions are given by Dividing equation (2) by equation (1), Example 9.7.10 A handball player throws a ball from point 'A' with a velocity 'v' in horizontal direction. Knowing that d = 4.5 m, determine i) The value of 'v' for which ball will strike the corner 'C'. ii) The range of values of 'v' for which the ball will strike the corner region BCD. Refer Fig 9.7.5. Solution: Equation of path is ⸫ Range of values is 9.805 m/s ≤ v ≤ 12.866 m/s Example 9.7.11 An enemy aircraft is sighted directly overhead at an altitude of 500 m flying at 540 km/h. At what angle a projectile should be launched so as to hit the aircraft? How much time will the projectile take to hit the aircraft? Take speed of projectile to be 1000 ms. Solution : To hit the aircraft, the x and y co-ordinates of both must be same. x = 150 t = 1000 cos α × t α = 81.373° For projectile, ⸫ t = 201.06, 0.507 ⸫ Projectile can hit the aircraft at 0.507 s when it is going up or at 201.06 s when it is coming down. ⸫ The aircraft will be hit at t = 0.507 s Example 9.7.12 A stone is thrown horizontally from a tower at A and hits the ground at B 4 seconds later. If the line of sight from A to B makes an angle of 40° with the horizontal, determine the initial velocity of the stone. Solution : ⸫ Height of the tower is 78.48 m For x-direction, ⸫ From equation (1), u = 23:38 m/s Example 9.7.13 A man standing in a horizontal tunnel of 3.8 m diameter throws a stone from a point 'A' as shown in Fig. 97.7. Determine maximum possible distance x knowing that initial velocity of projection is 12 m/s. Solution: The maximum height reached by the projectile is H = 3.8 - 1.4 = 2.4 m. Example 9.7.14 Measurements of a shot recorded on a video tape during a basket ball are shown in the Fig. 9.7.8. The ball passed through the loop C after just clearing the hand of player B, who tried to block it. Neglecting the size of ball, determine the magnitude VA of its initial velocity and height 'h' when it passes over player B. Solution: For motion from A to C, x = 9 m, y = 1 m u = vA, α = 30° For motion from A to B, x = 7.5 m, y = h - 2 u = 11.236 m/s, α = 30° Example 9.7.15 A shot is fired at 60 m/s at an angle of elevation 60°. State the position of shot after 2 seconds and its velocity at that instant. Solution : u = 60 m/s, α = 60°, t = 2 s vx = u cos α = 60 cos 60 ⸫ vx = 30 m/s x = vx · t = 30 × 2 ⸫ x = 60 m Example 9.7.16 A player throws a ball from point A as shown in Fig. 9.7.9 with velocity 18 m/s. Determine maximum height 'h' at which ball can strike the wall and corresponding angle α. Solution : Example 9.7.17 A player throws a ball with velocity vo = 16 m/s from point A as shown in Fig. 9.7.10. Determine the highest point B where ball will strike the wall. Solution: The maximum height reached by the ball above A is H = 6 - 1.5 = 4.5 m. Example 9.7.18 A ball is projected with an initial velocity of u at an angle of a with the horizontal. If the initial velocity is 10 m/s and α = 45o, find the time of flight, maximum height attained and horizontal range. Solution : Example 9.7.19 A bullet is fired making an angle of 30° to the horizontal from a hill which strikes the target which is 80 m lower than the horizontal passing through the firing point as shown in Fig. 9.7.11. The initial bullet velocity is 100 m/s. Find the following : i) The maximum height above horizontal to which the bullet will rise. ii) The velocity of bullet when it strikes the target. iii) The total time required for the bullet when it strikes the target. Solution : Example 9.7.20 A baseball pitching machine Fig. 9.7.12 "throws" baseballs with a horizontal velocity vo. Knowing that height h varies between 0.8 m and 1 m, determine (i) The range of values of vo, (ii) The values of a corresponding to h = 0.8 m and h = 1 m. Solution: (i) The equation of path is Where θ = angle of projection For h = 0.8 m Example 9.7.21 A stone is projected with a speed of 30 m/s at an angle of elevation of 50°. Find its velocity (1) after 2 seconds, (ii) at higher point of its path, (iii) at the height of 6 m. Find alsothe time interval between two points at which the stone attains a speed of 25 m/s. Solution : u = 30 m/s, α = 50° Maximum height is, ⸫ H = 26.918 m At the highest point (C) vy = 0 and velocity along x remains constant. ⸫ vx at C = u cos α = 30 cos 50 ⸫ vx = 19.283 m/s For velocity after 2 sec (at point B). For velocity at the height of 6 m, Examples for Practice Q.1 A ball is to be thrown from point A to B. Determine the smallest value of the initial velocity vo and the corresponding angle a so that the ball reaches B. Refer Fig. 9.7.14. [Ans. : vo = 3.97 m/s, α = 28.16] Q.2 A target is fired with an initial velocity of 240 m/s at a target located 600 m above the gun and at a horizontal distance. of 3600 m. Neglecting air resistance, determine the value of the firing angle α. [Ans. : α = 29.86° or 69.59°]

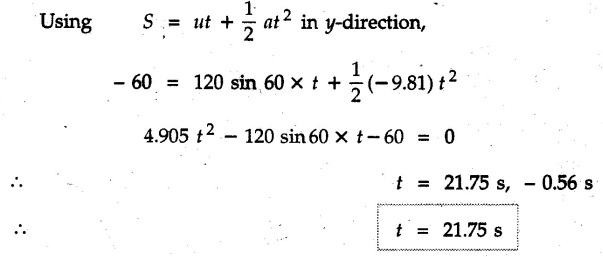


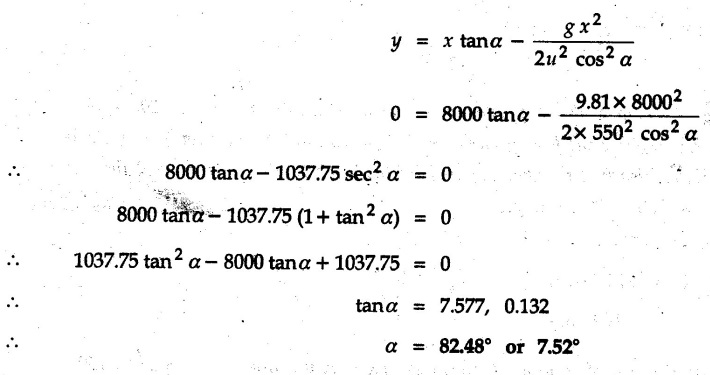
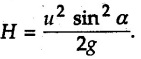
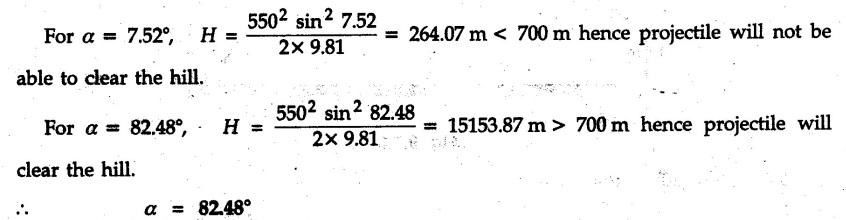
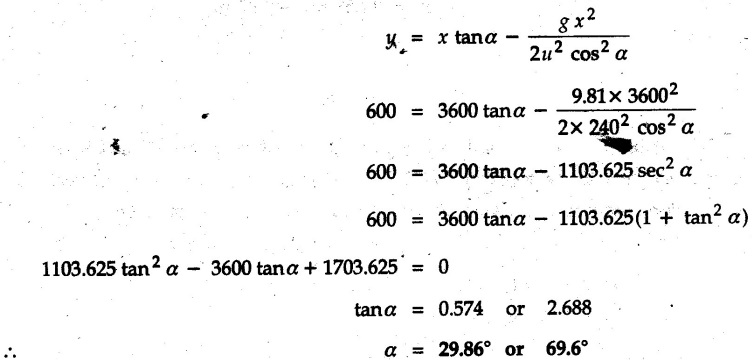

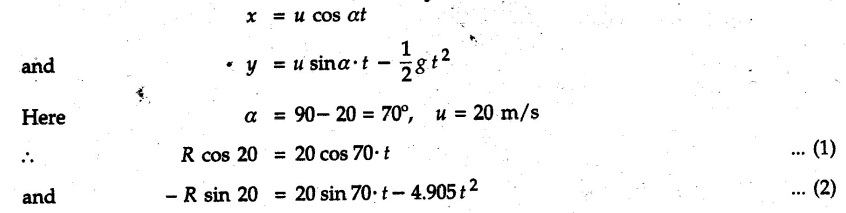
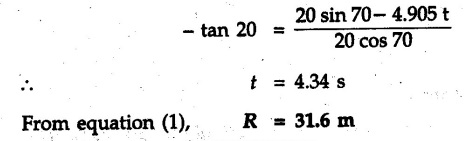

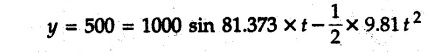
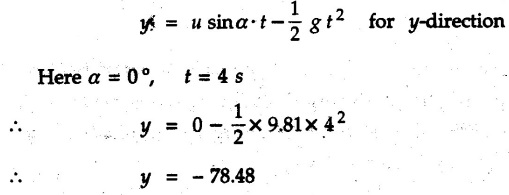
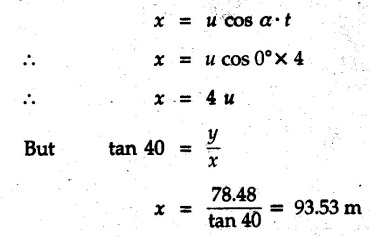

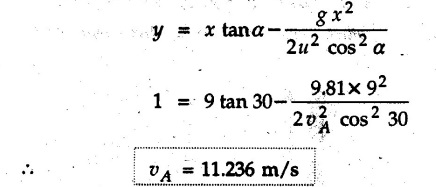
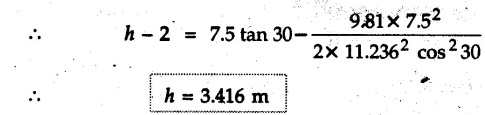


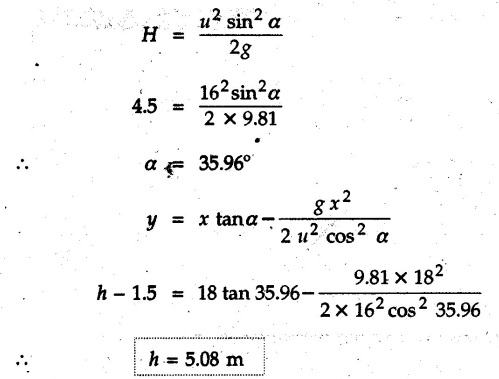


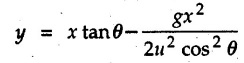
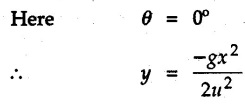

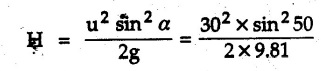
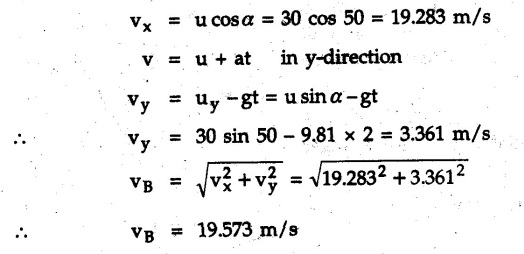

Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : - Solved Example & Practice Problems: Projectile Motion
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
