Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies
Solved Example & Practice Problems: Equilibrium of Coplanar Non-Concurrent Force System
Examples for Practice, Solved Example Problems : Equilibrium of Coplanar Non-Concurrent Force System : Equilibrium of Rigid Bodies - Engineering Mechanics
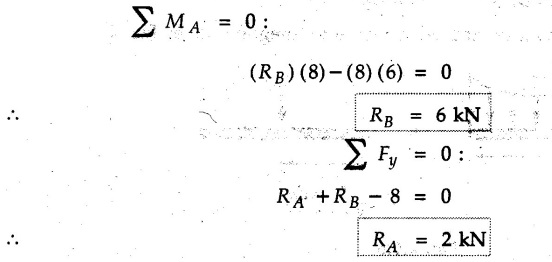
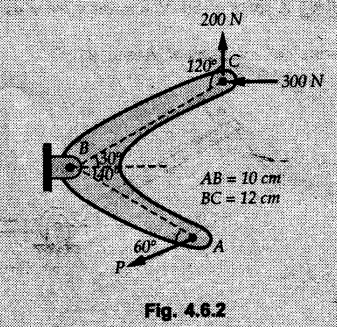
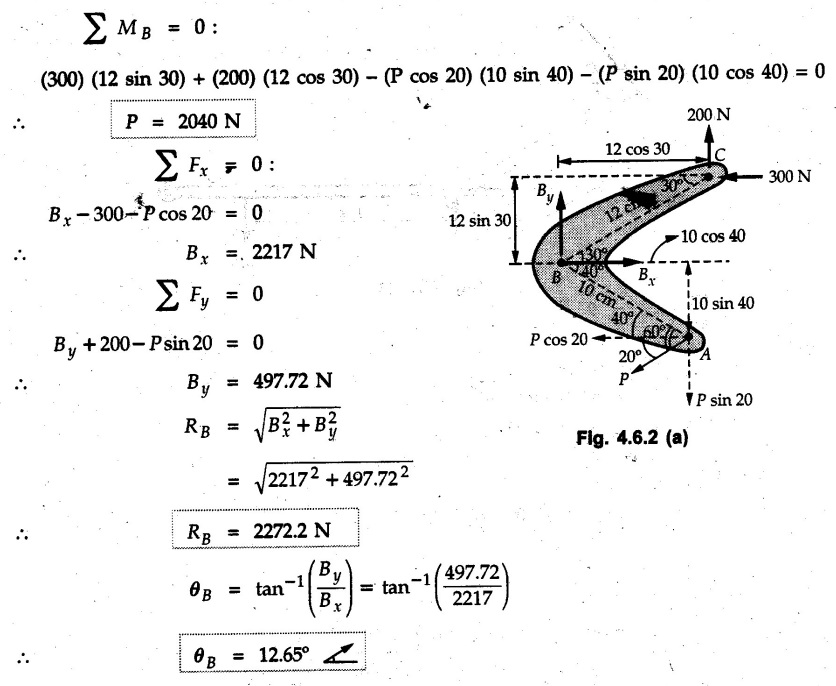
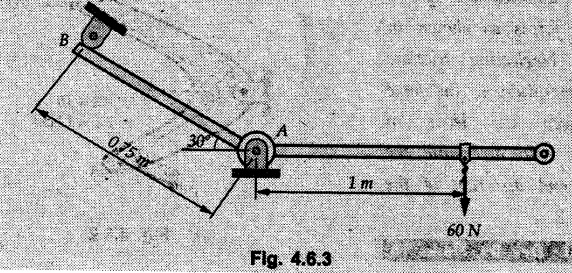
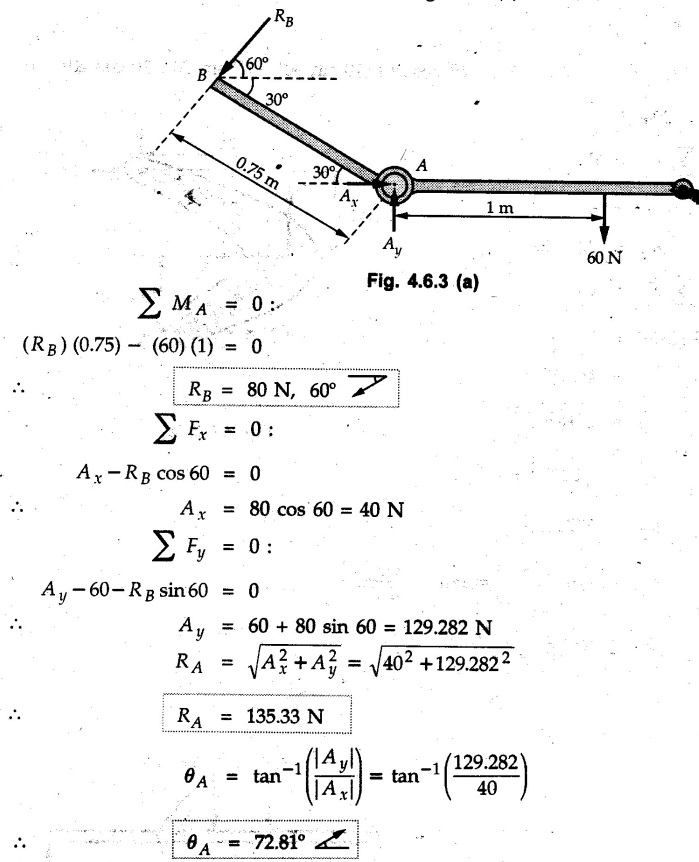
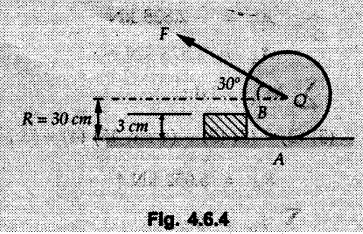
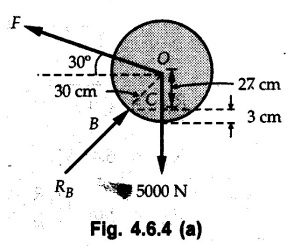
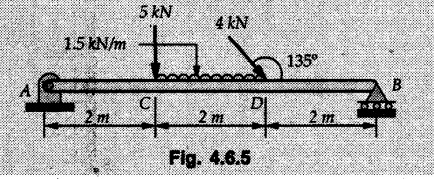
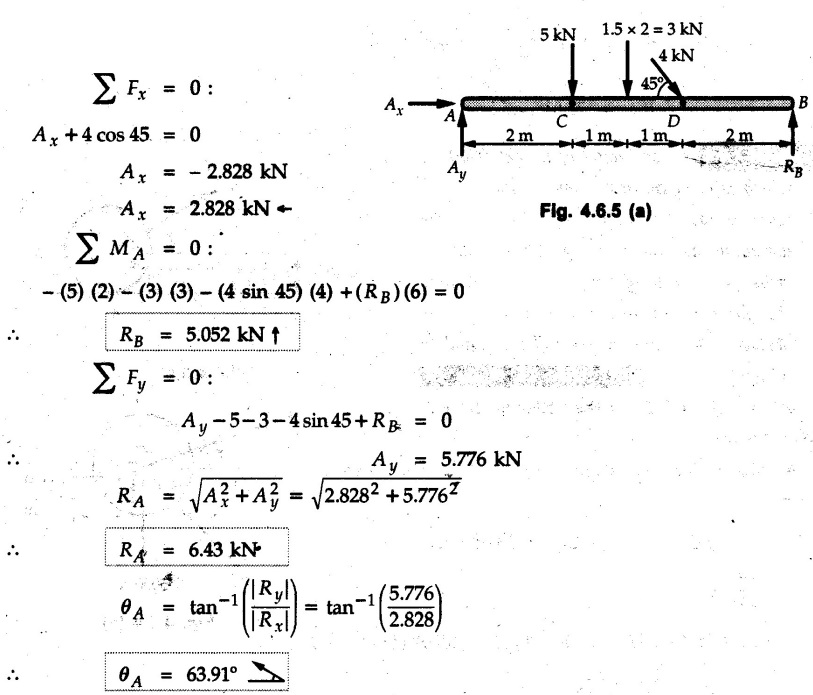
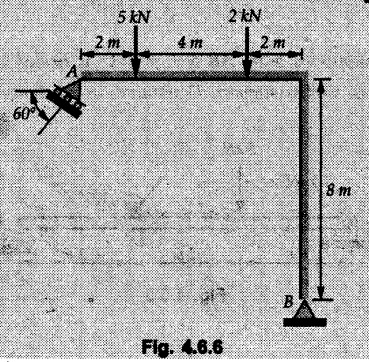
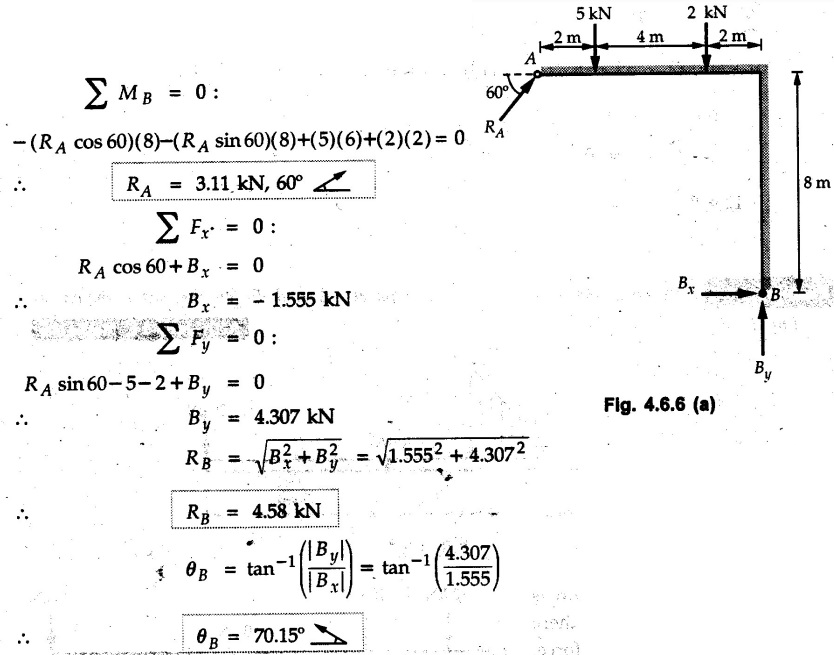
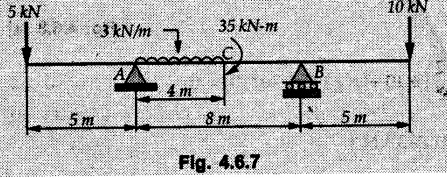
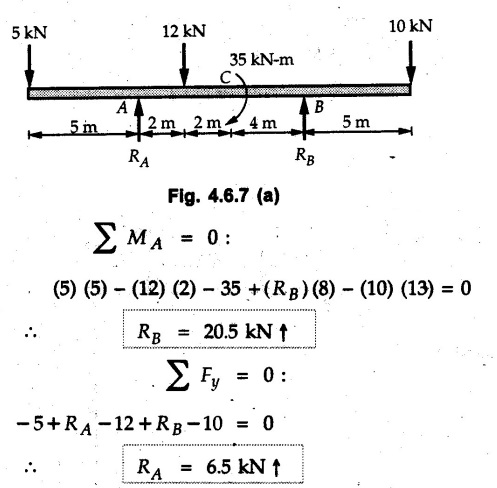
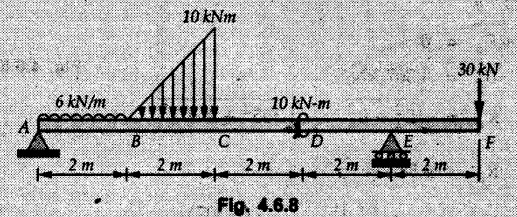
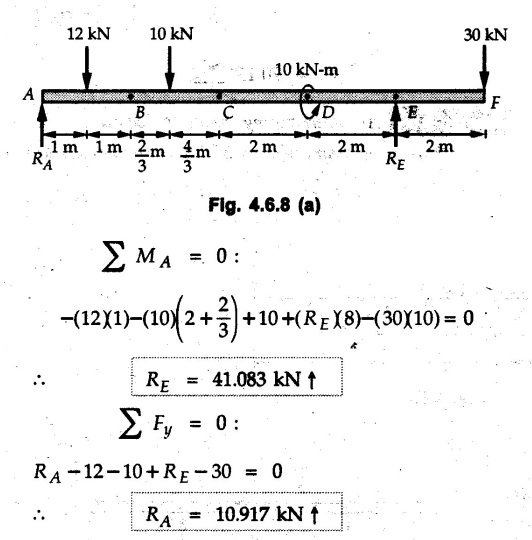
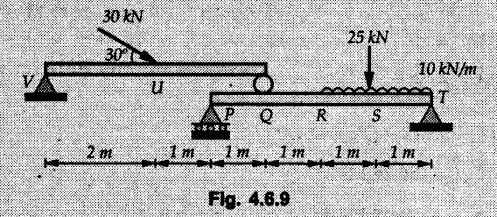
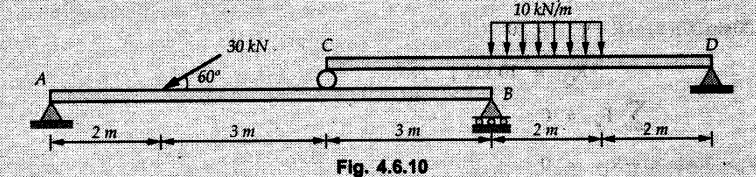
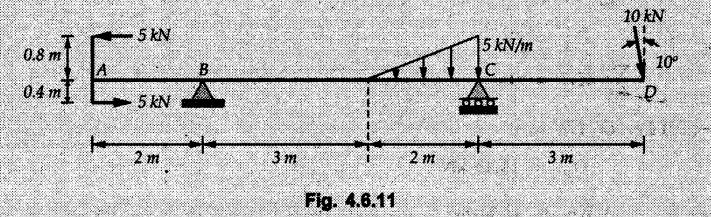
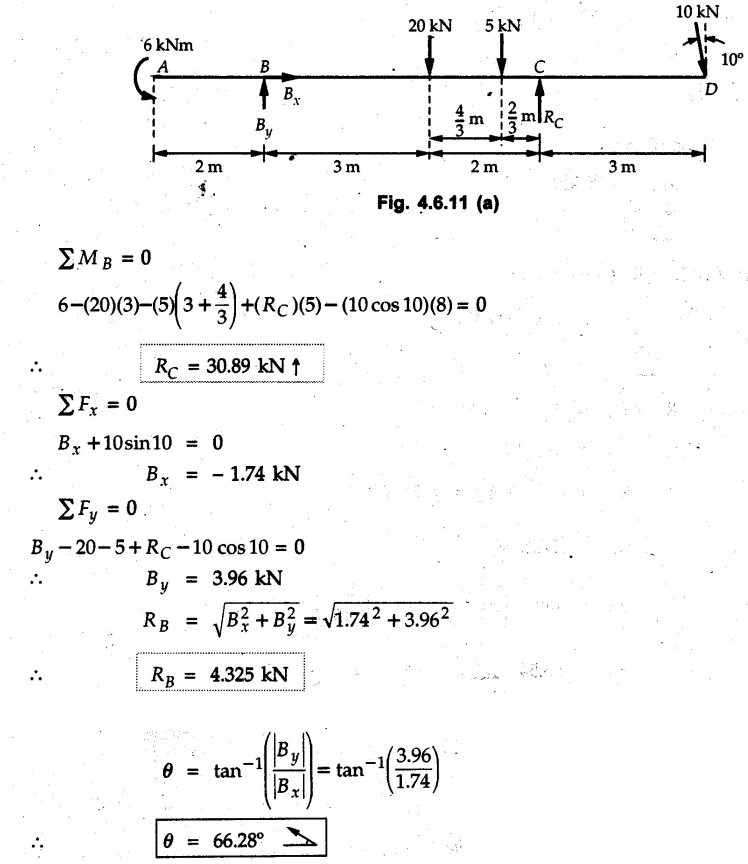
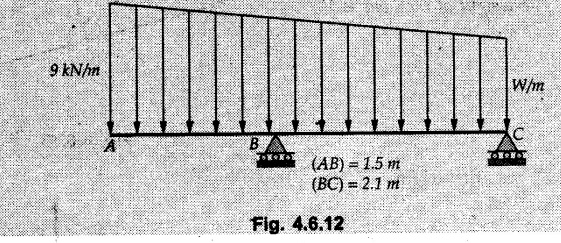
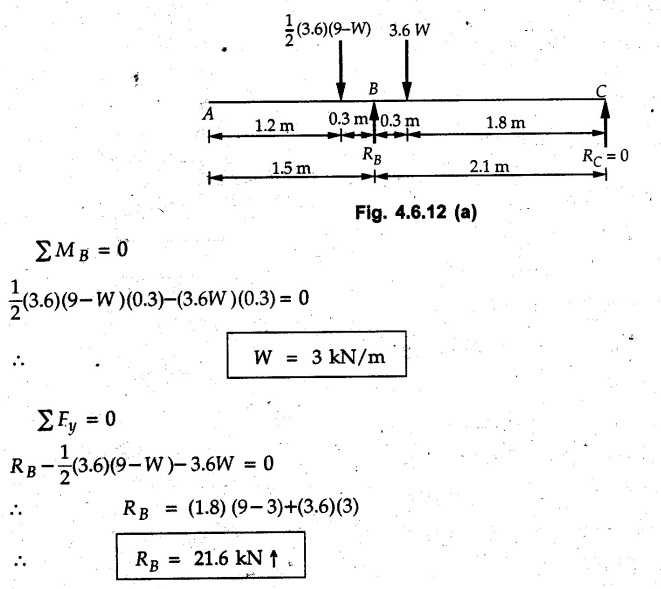
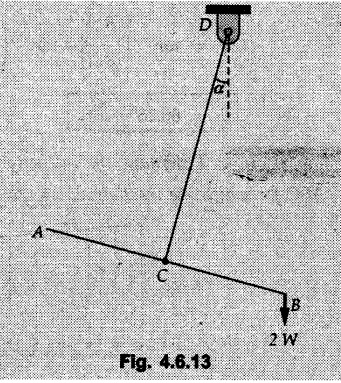
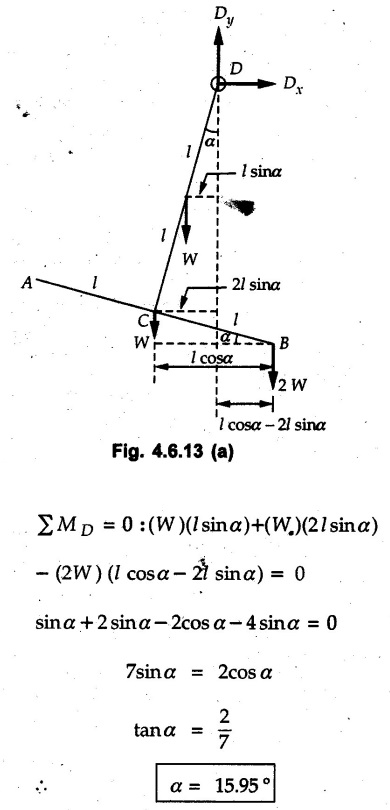
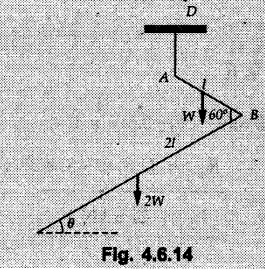
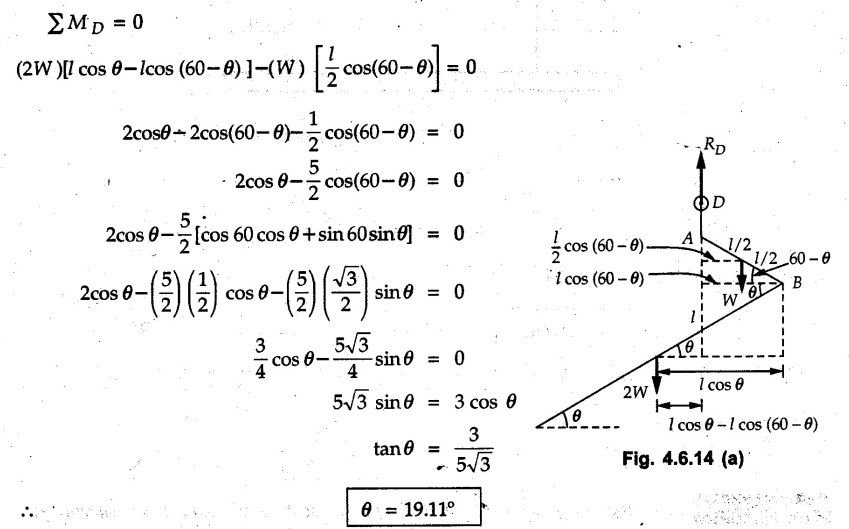
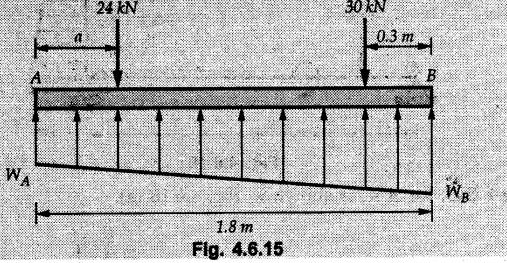
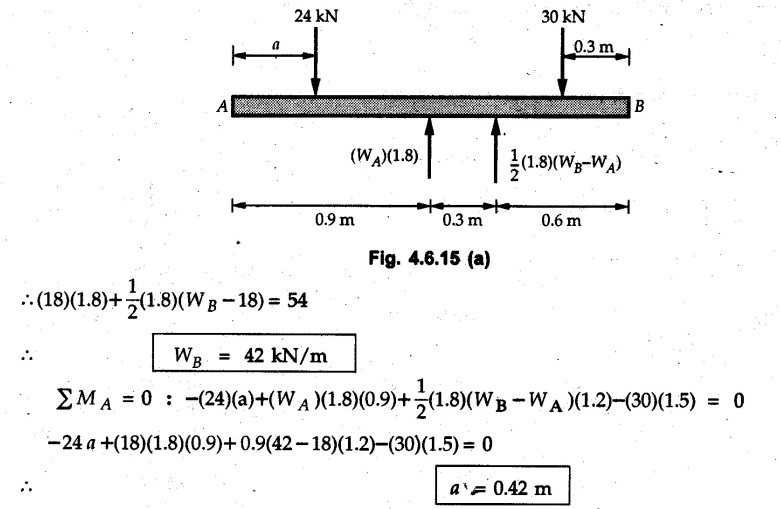
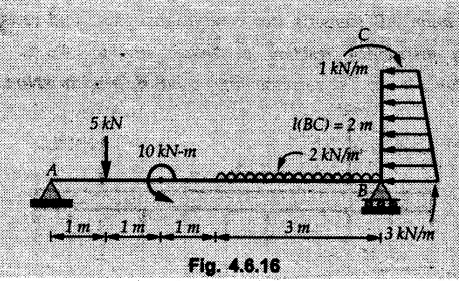
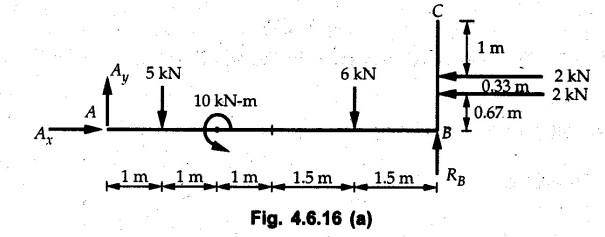
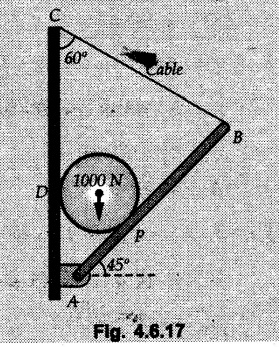
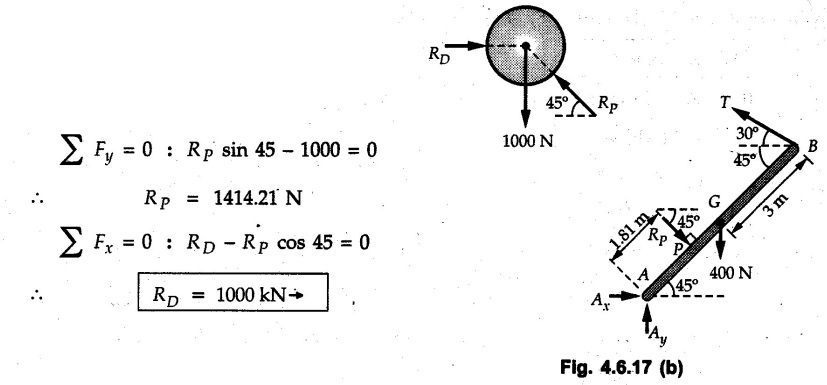
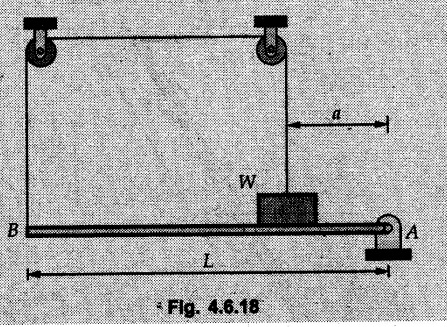
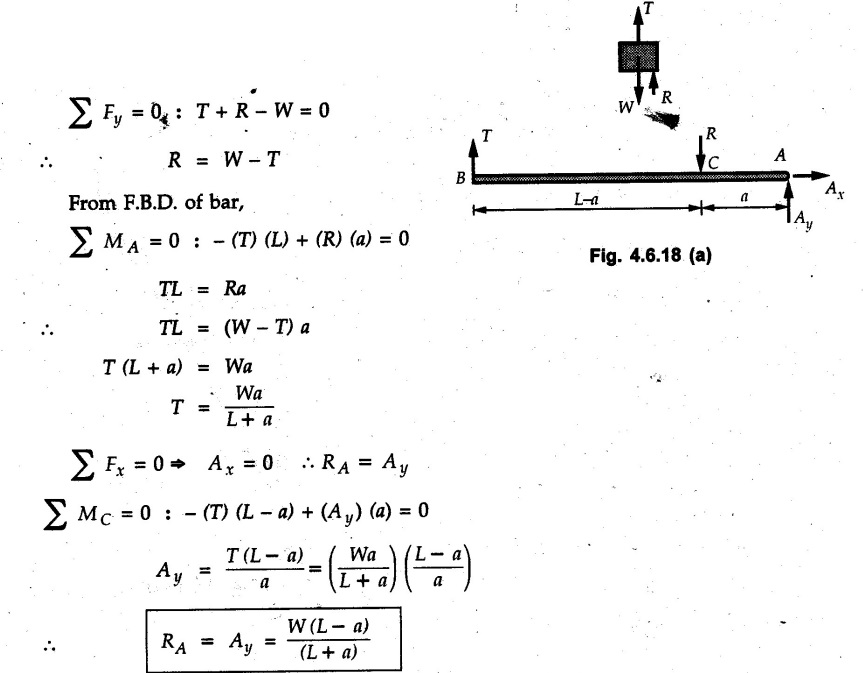
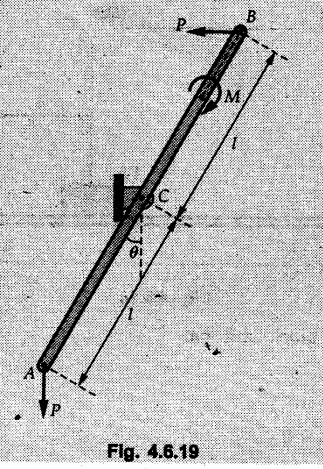
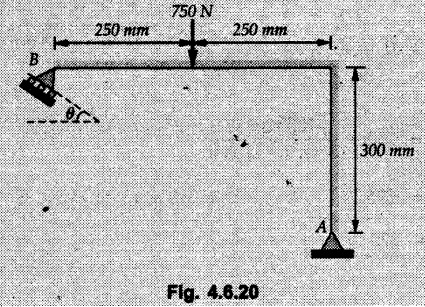
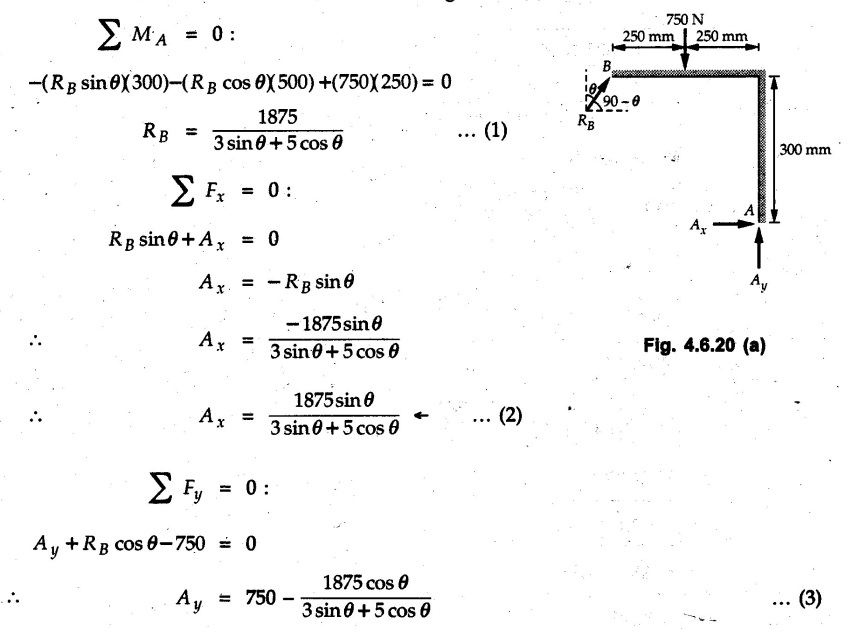
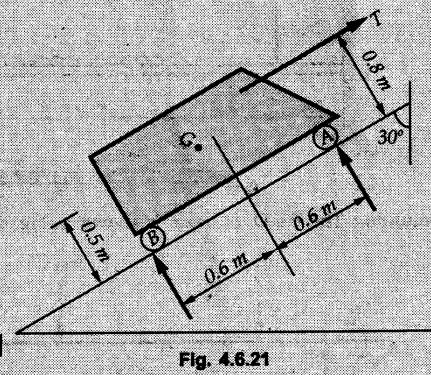
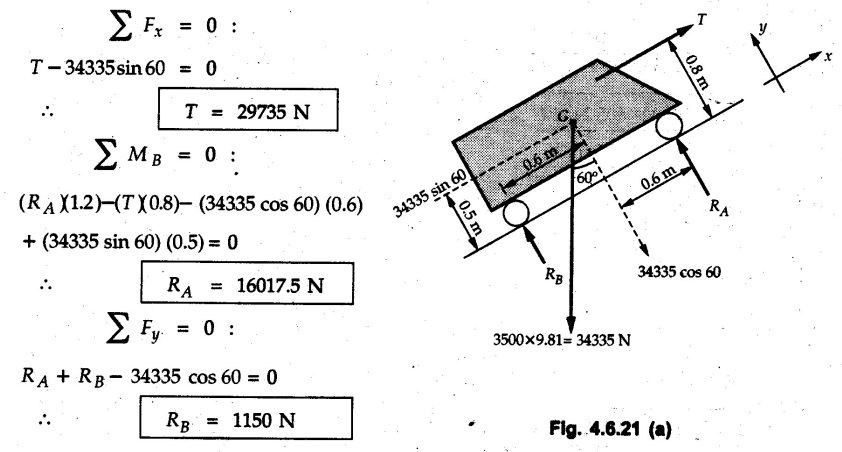
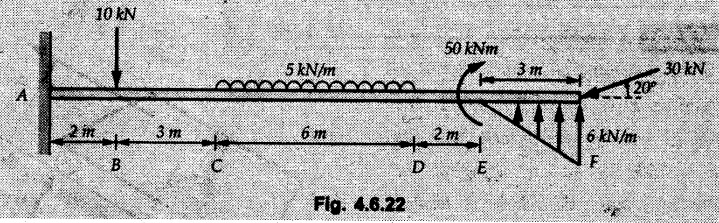
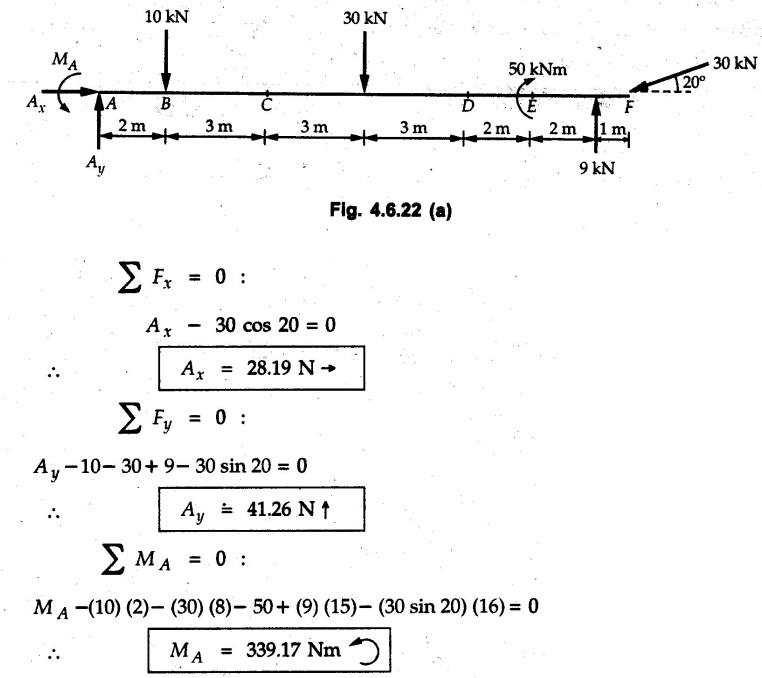
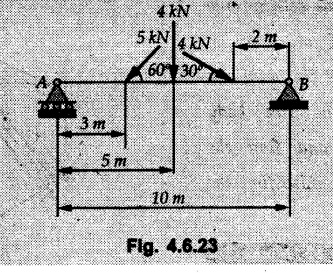
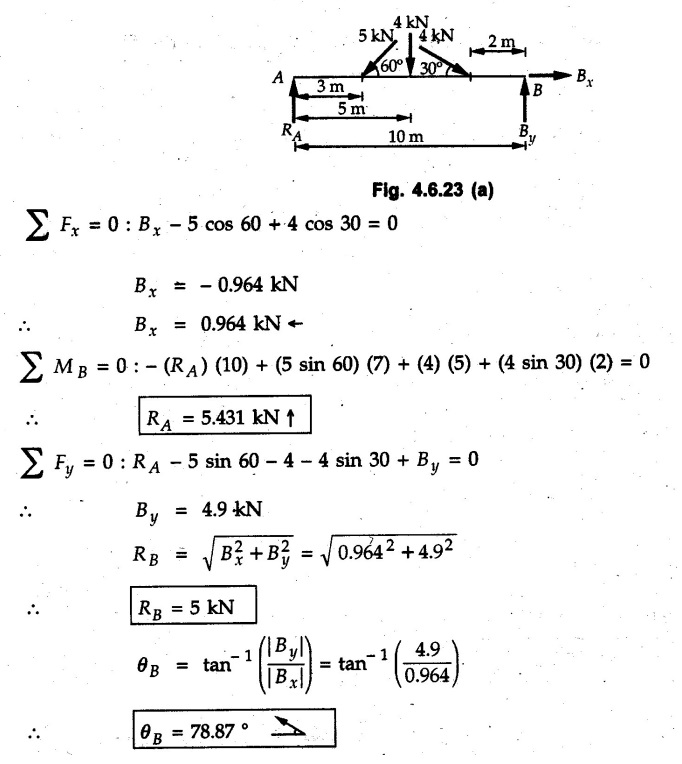
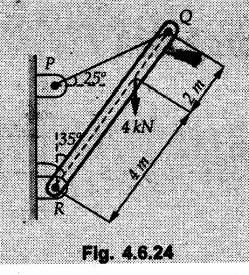
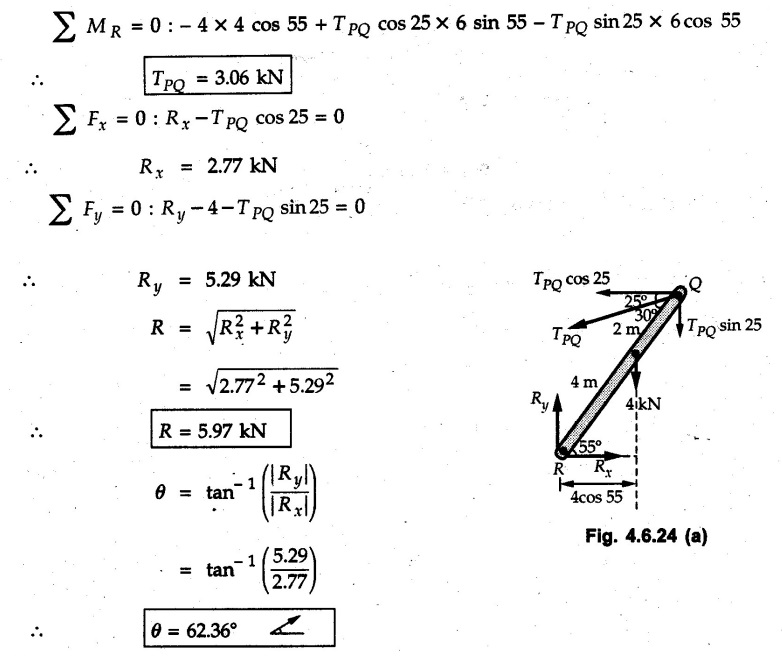
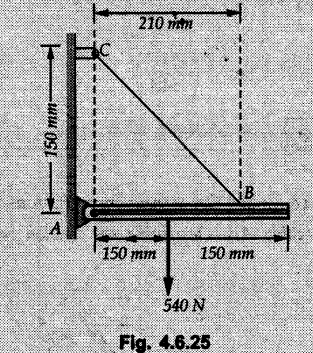
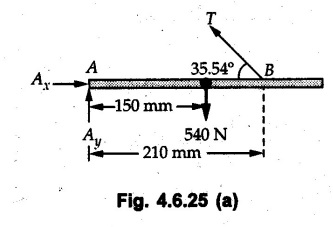
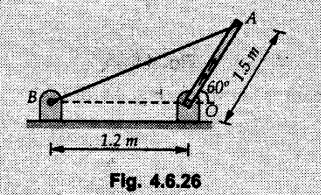
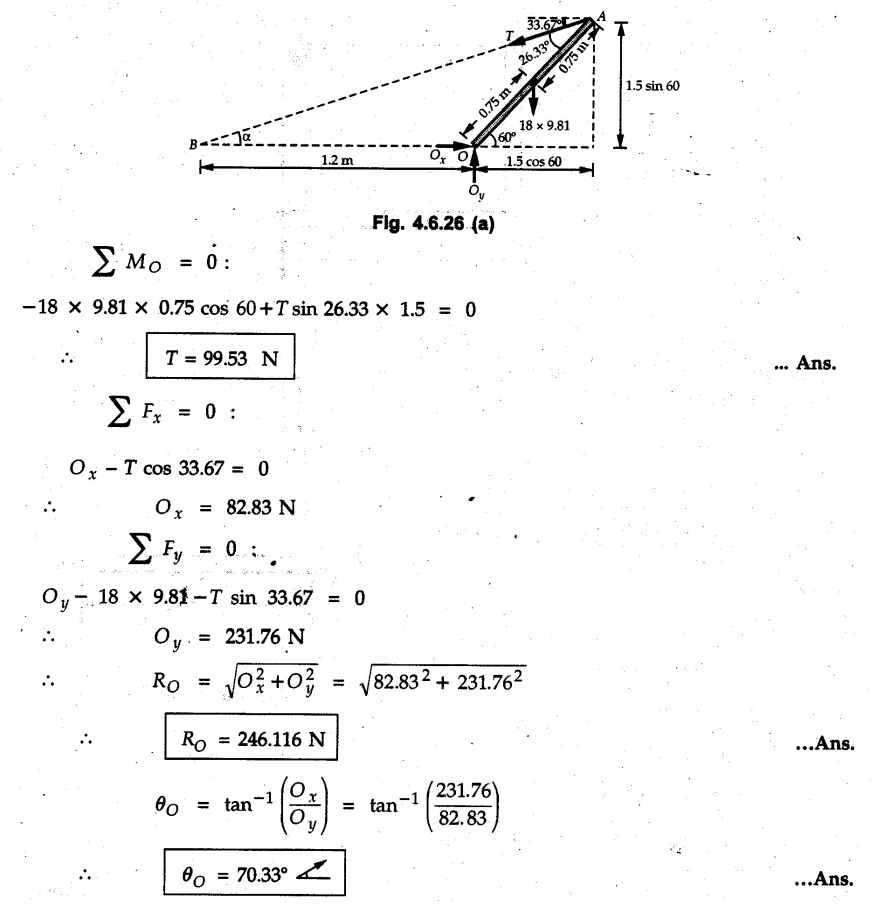
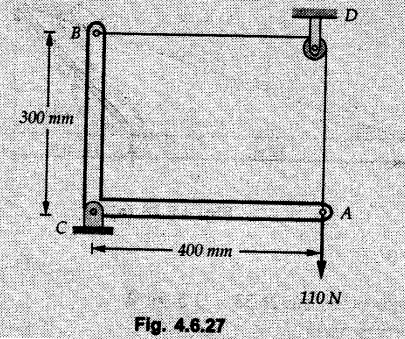
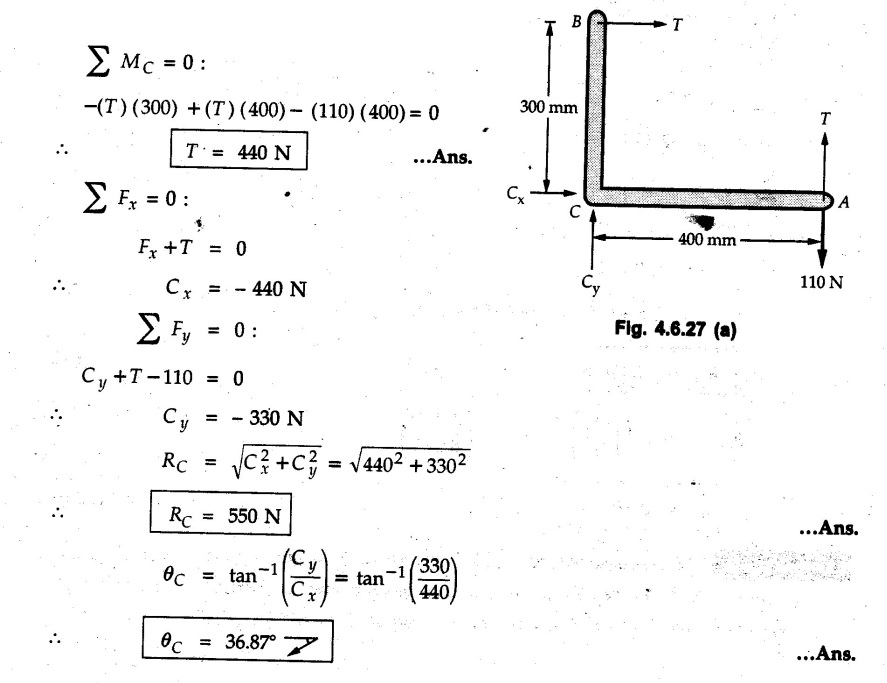
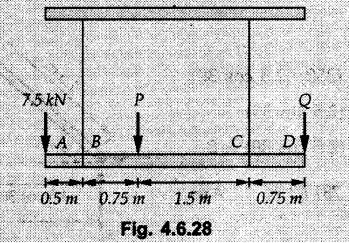
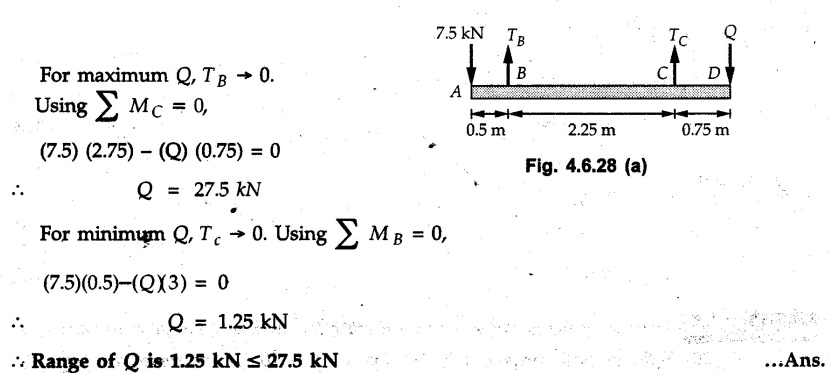
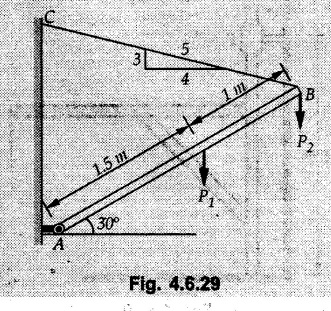
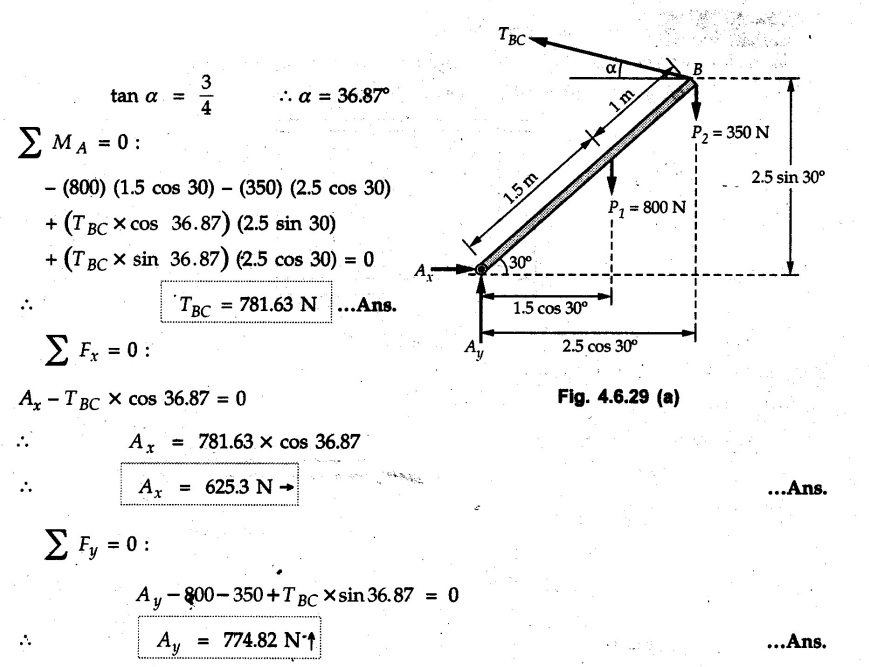
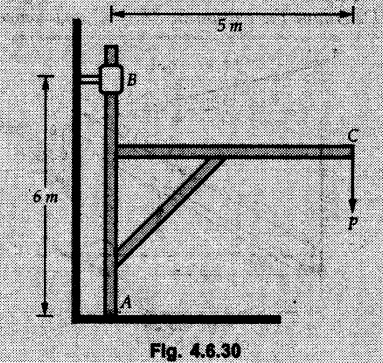
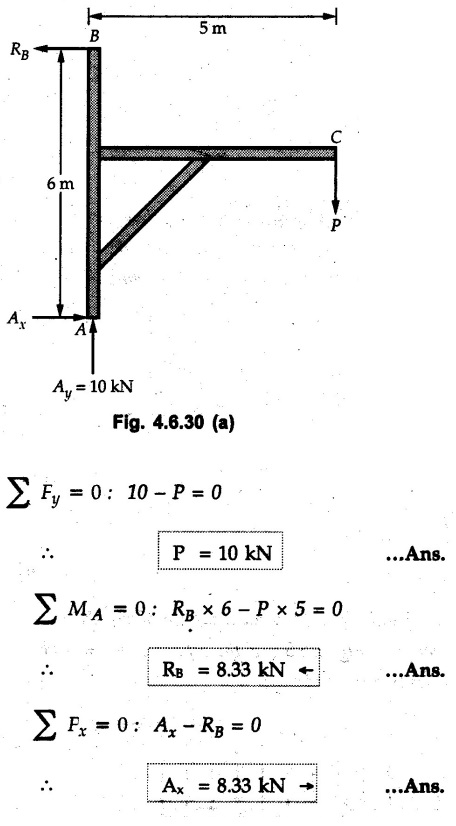
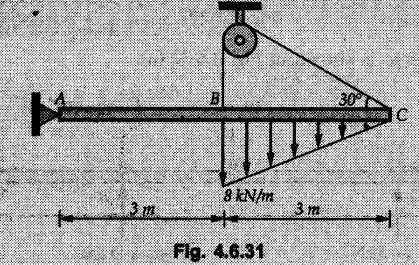
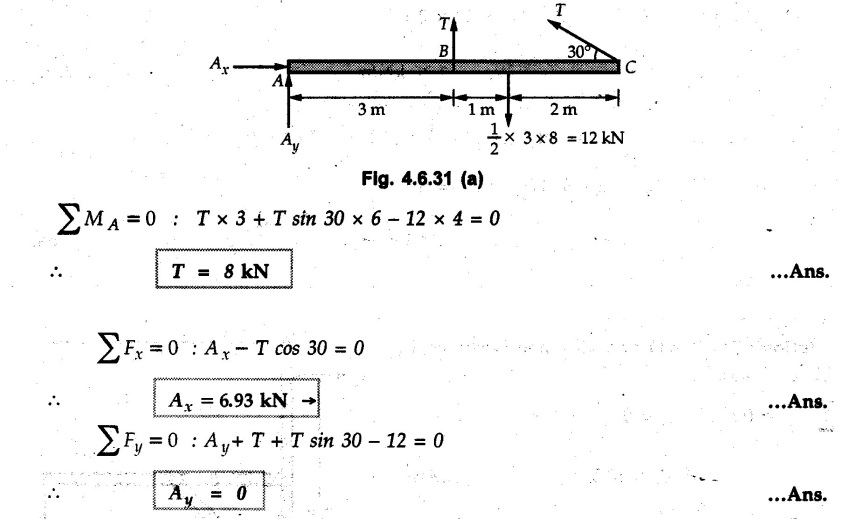
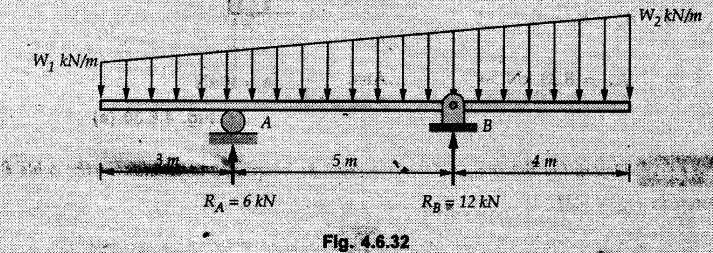
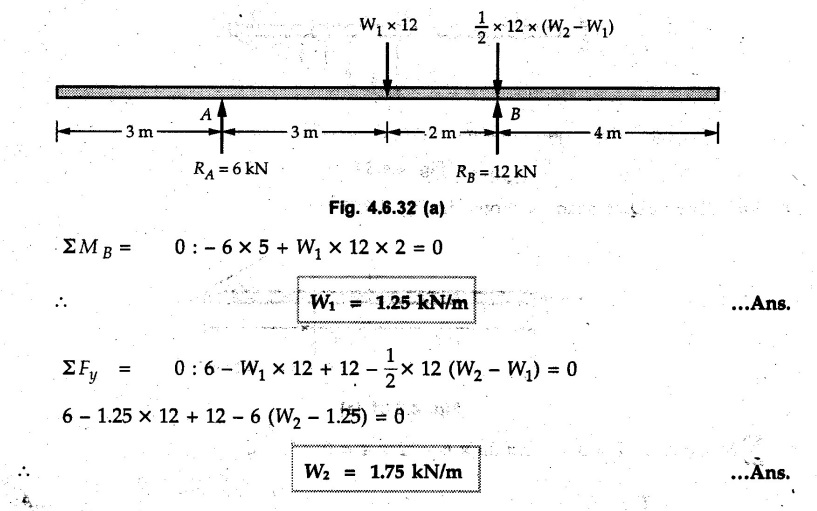
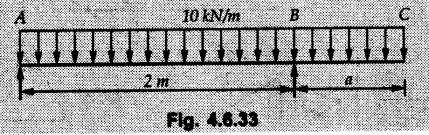
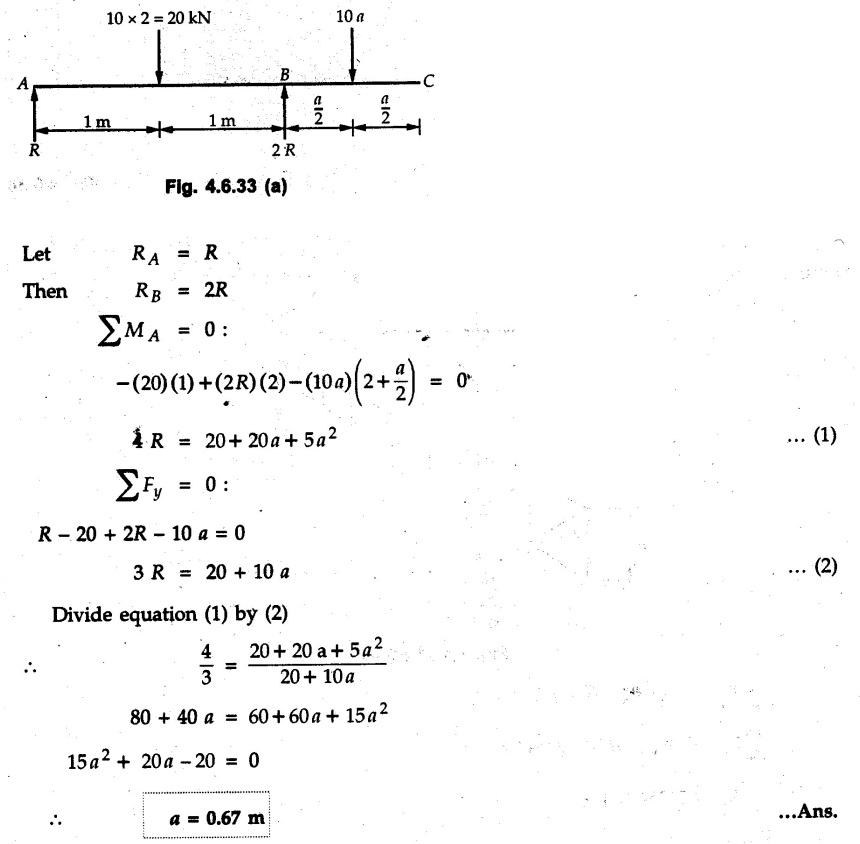
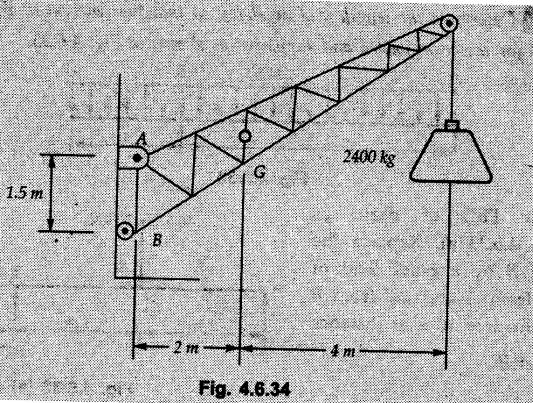
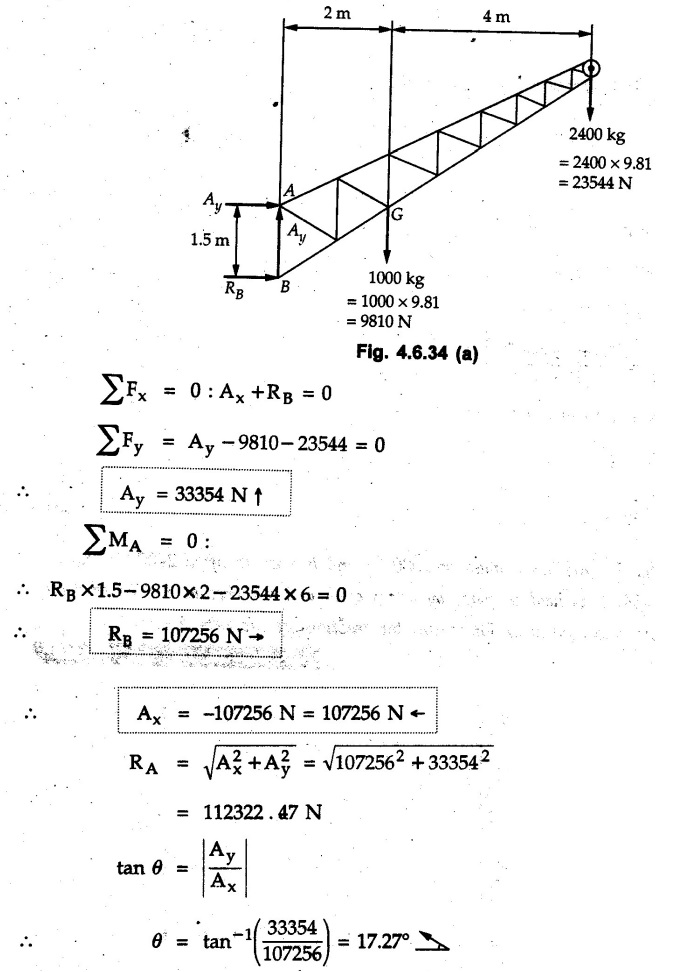
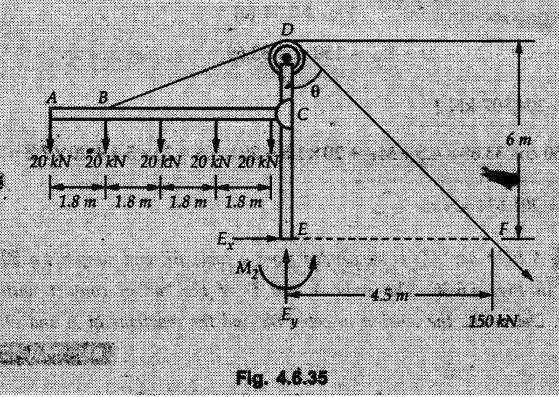
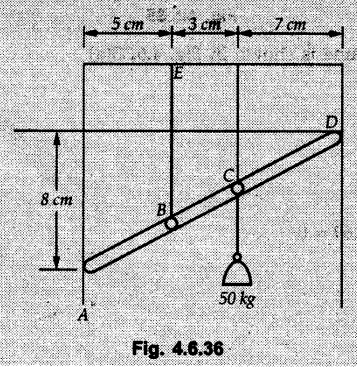
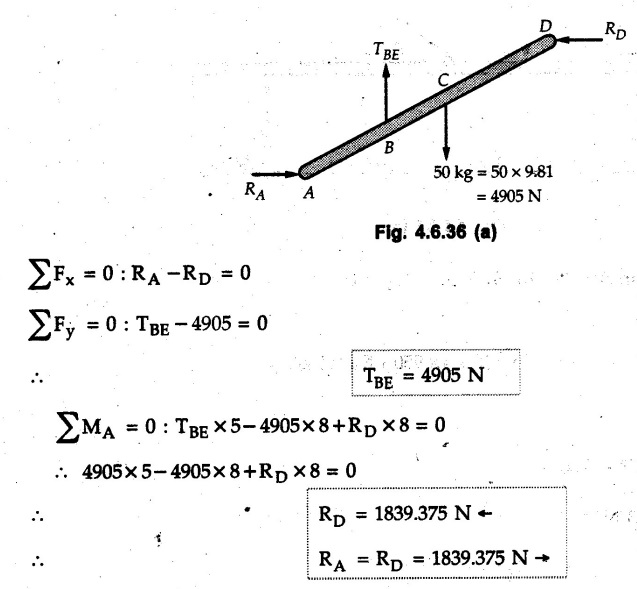
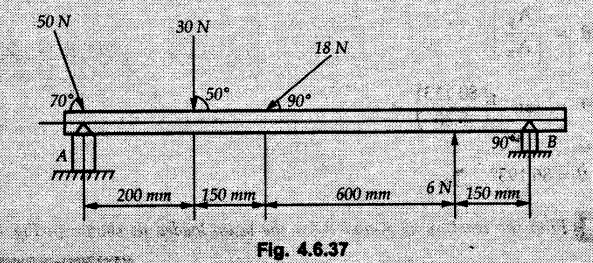
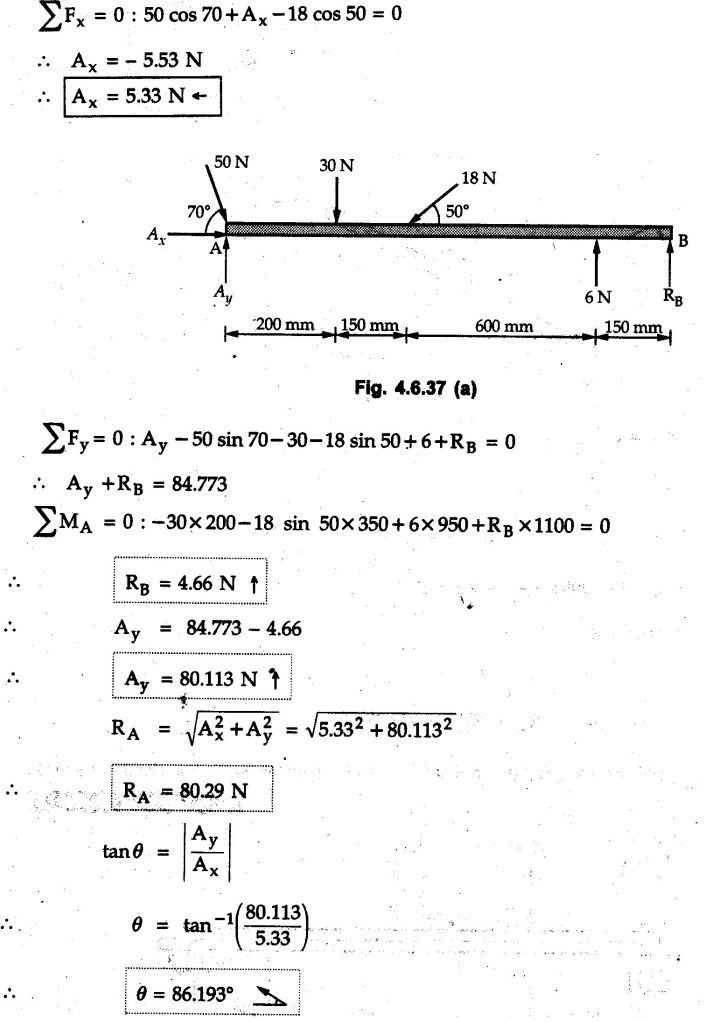
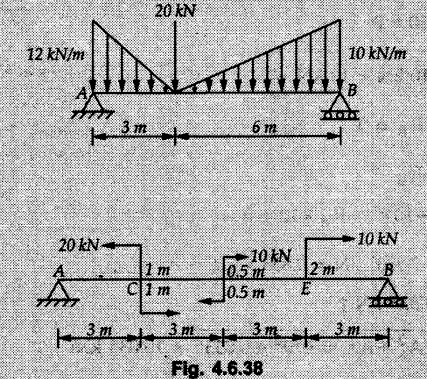
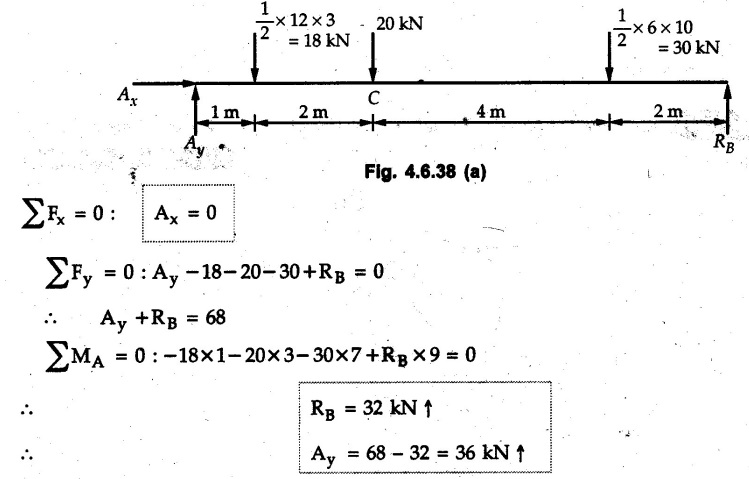
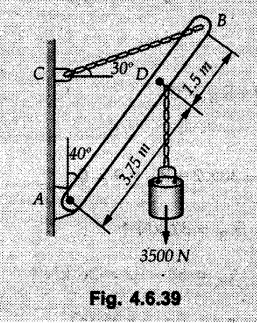
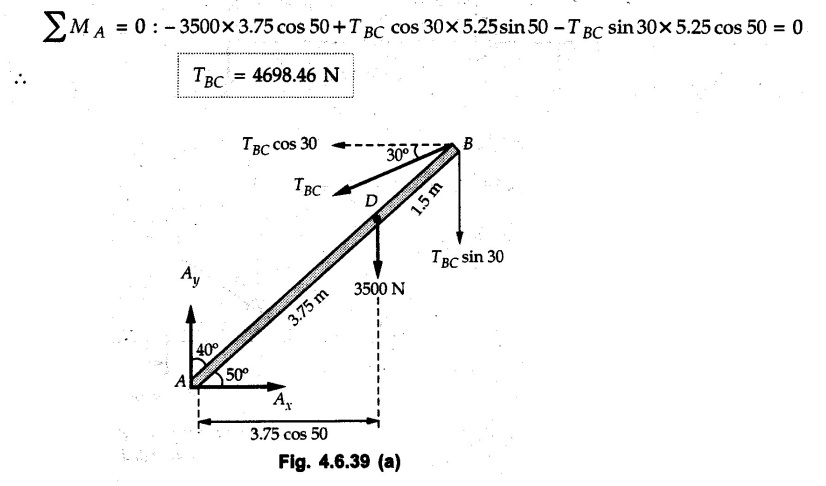
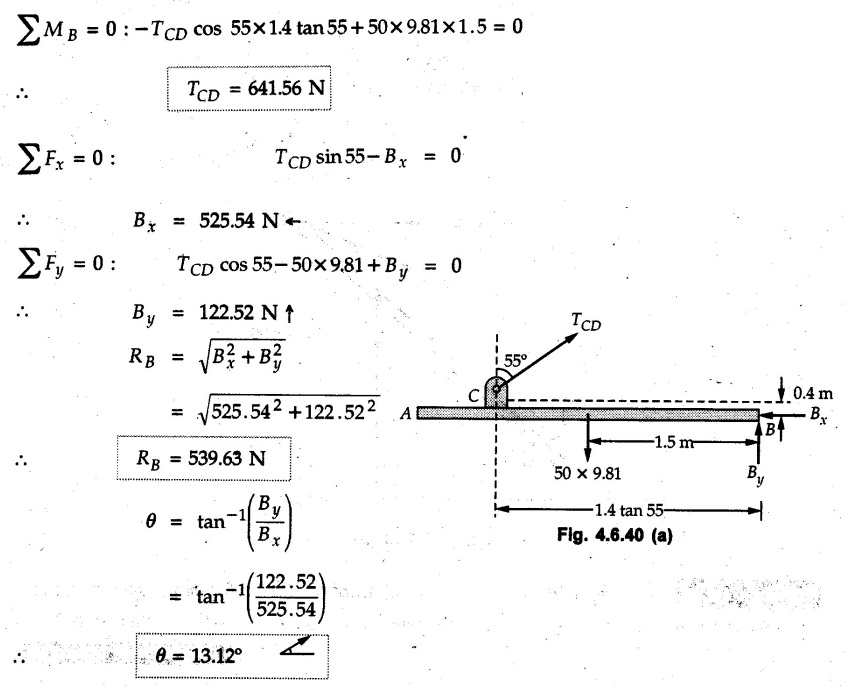
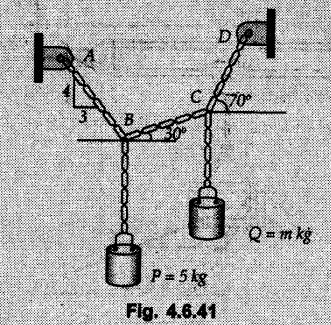
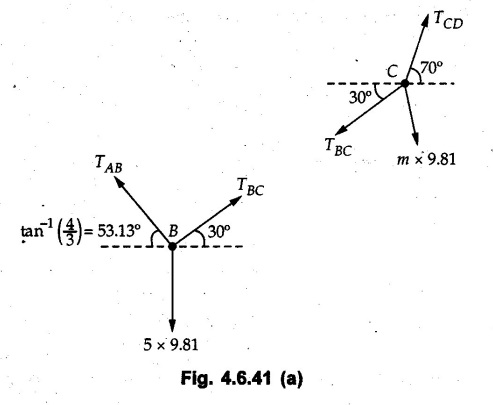
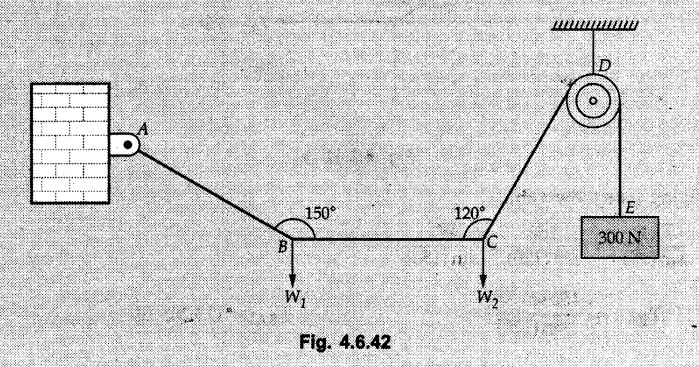
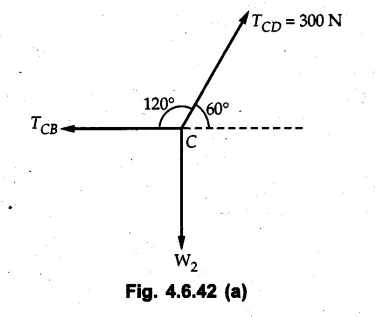
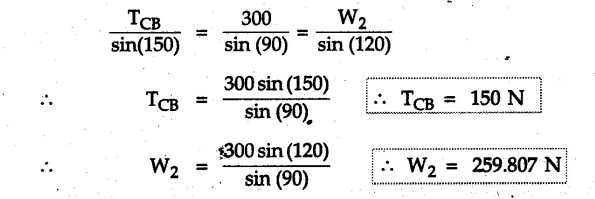
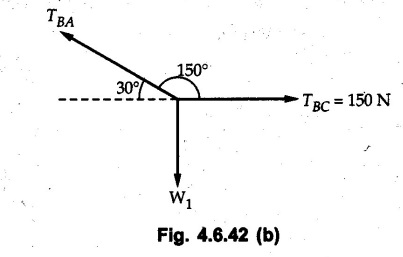
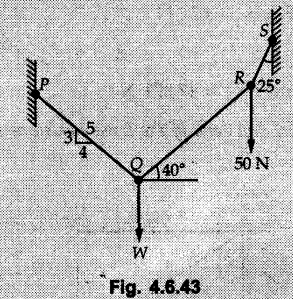
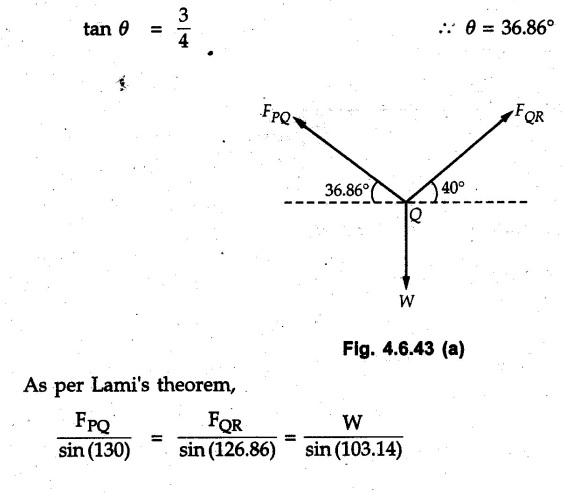
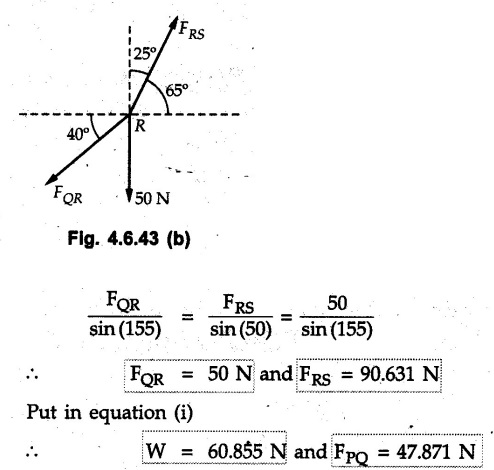
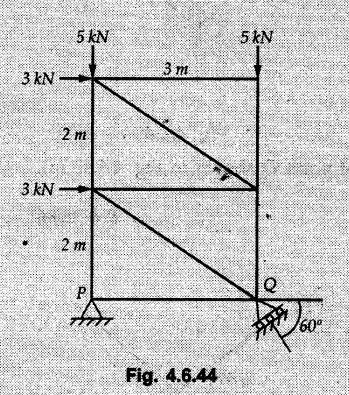
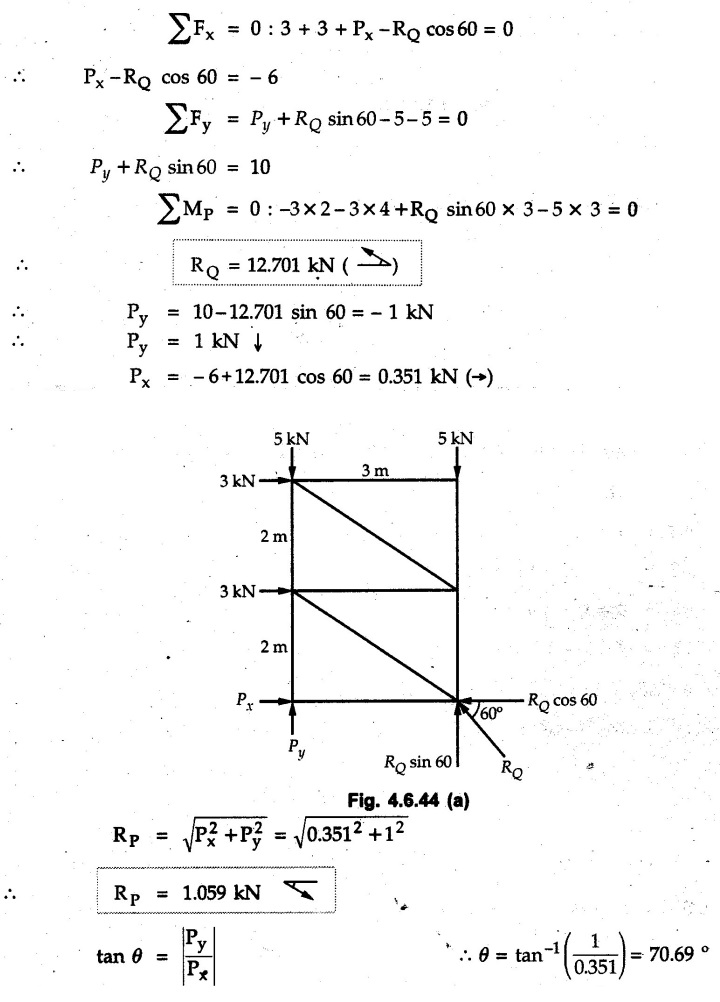
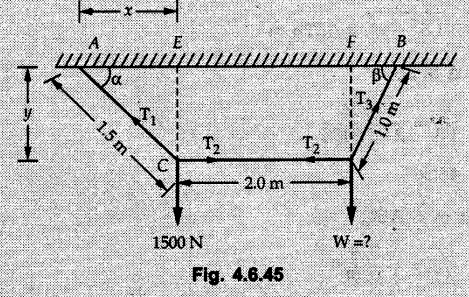
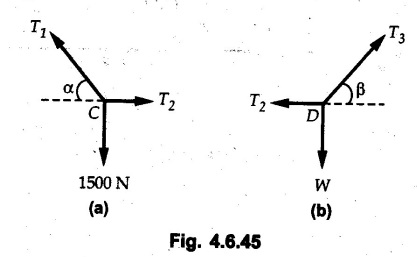
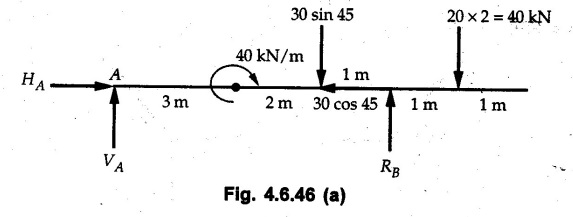
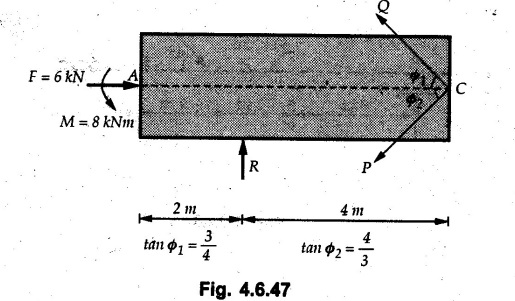
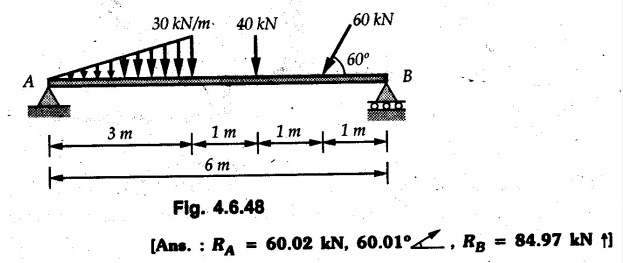
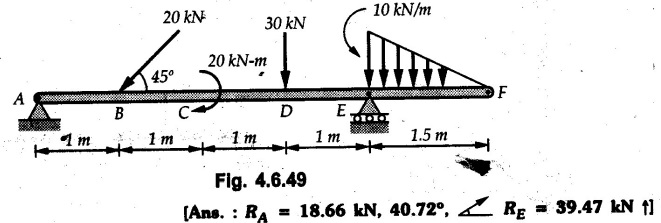
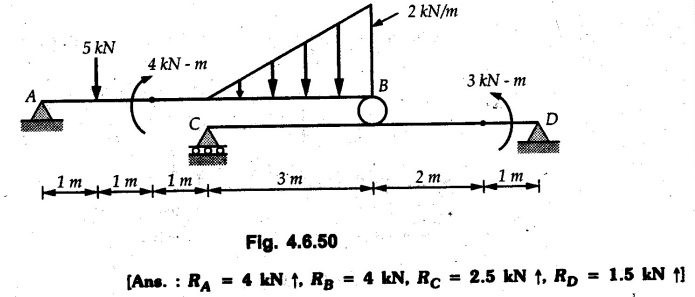
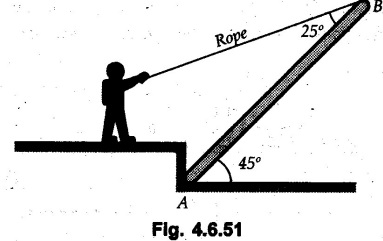
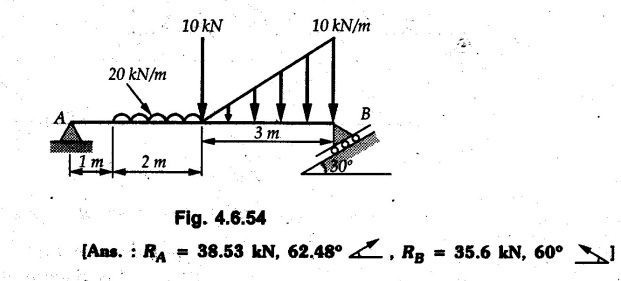
Solved Examples for Understanding Example 4.6.1 Find RA and RB for the beam shown in Fig. 4.6.1. Solution : Example 4.6 2 The lever ABC of a component of a machine is hinged at B and is subjected to a system of coplanar forces as shown in Fig. 4.6.2. Neglecting friction. Find the magnitude of the force (P) to keep the lever in equilibrium. Also determine the magnitude and direction of the reactions at B. Solution: The F.B.D. of lever ABC is shown in Fig. 4.6.2 (a). Example 4.6.3 A force of 60 N acts on a lever as shown in the Fig. 4.6.3. Determine the reactions at A and B. Solution: The F.B.D. of lever is shown in Fig. 4.6.3 (a). Example 4.6.4 A road roller of weight 5000 N, which is of cylindrical shape, is pulled by a force F at an angle of 30° with the horizontal as shown in Fig. 4.6.4. It has to cross an obstacle of height 3 cm. Calculate the force F required to just cross this obstacle. The radius of the roller is equal to 30 cm. Solution: The F.B.D. of the roller is shown in Fig. 4.6.4 (a). As the roller just starts moving over the obstacle, RA → 0 Note This problem can also be solved using the method of equilibrium of three forces in a plane. Example 4.6.5 A simply supported beam AB of 6 m span is loaded as shown in Fig. 4.6.5. A is a hinged support, B is a roller support. Determine the reactions at A and B. Solution: The F.B.D. of beam is shown in Fig. 4.6.5 (a). Example 4.6.6 A frame is loaded as shown in Fig. 4.6.6. Find the support reactions. Solution: The F.B.D. of the frame is shown in Fig. 4.6.6 (a). Example 4.6.7 An overhanging beam is loaded as shown in Fig. 4.6.7. Find the support reactions of the beam when a 35 KN-m couple acts at C as shown. Solution: The F.B.D. of the beam is shown in Fig. 4.6.7 (a). As there is no horizontal component of applied force, the horizontal component of reaction at A is zero. Example 4.6.8 Determine the reactions at the supports A and E for the beam shown in Fig. 4.6.8. Solution: The F.B.D. of beam is shown in Fig. 4.6.8 (a). As there is no horizontal applied force, A the reaction at A is vertical. Example 4.6.9 Determine the reactions at the supports P, Q, T and V for the beam subjected to loading as shown in the Fig. 4.6.9. Solution: Free body diagrams of the two beams are shown in Fig. 4.6.9 (a). Example 4.6.10 Two beams AB and CD are shown in Fig. 4.6.10. A and D are hinged supports. B and C are roller supports. 1) Sketch the free body diagram of the beam AB and determine the reactions at the supports A and B. ii) Sketch the free body diagram of the beam CD and determine the reaches at the supports C and D. Solution: The free body diagrams of AB and CD are shown in Fig. 4.6.10 (a). Example 4.6.11 A beam 'ABCD' having self weight 2 kN/m is subjected to additional load as shown in Fig. 4.6.11. Find the support reaction at 'B' and 'C'. Solution: The two forces of 5 kN form a couple of moment 5×1.2 = 6 kNm. The weight of beam is 2 × 10 = 20 kN acting at the centre. The F.B.D. of beam is shown in Fig. 4.6.11 (a). Example 4.6.12 Determine the intensity of the distributed load W at the end C of the beam ABC for which the reaction at C is zero. Also calculate the reaction at B. Refer Fig. 4.6.12. Solution: The given load can be reduced to two point loads as shown in Fig. 4.6.12 (a). Example 4.6.13 Two identical prismatic bars AB and CD are welded together to form a rigid 'T' and suspended in a vertical plane as shown in Fig. 4.6.13. Calculate the angle a that the bar CD will make with the vertical when a vertical load of 2W is applied at B. The weight of each bar is W. Solution : F.B.D. of the rigid 'T' is. shown in Fig. 4.6.13 (a). Let l(AB) = l (CD) = 2l then weights of AB and CD act through their centres as shown in Fig. 4.6.13 (a). Example 4.6.14 Two identical prismatic bars AB and BC of lengths 1 and 21 respectively are rigidly joined at B and suspended by a string AD as shown in Fig. 4.6.14. Determine the position of equilibrium as defined by angle 0 that the bars will assume under the action of their weights W and 2W. Solution: The F.B.D. is shown in Fig. 4.6.14 (a). Example 4.6.15 The beam AB supports two concentrated loads and re exerts a linearly distributed reaction as shown in Fig. 4.6.15. If WA = 18 kN/m determine : i) Distance 'n' ii) The corresponding value of 'WB' in kN/m. Solution: The F.B.D. of beam AB is shown in Fig. 4.6.15 (a). (See Fig. 4.6.15 (a)) ΣFy = 0: (WĄ )(1.8) + 1/2(1.8)(WB −WĄ ) - 24 - 30 = 0 Given WA = 18 kN/m Example 4.6.16 Find the reaction at A and B for a bent ABC loaded as shown in Fig. 4.6.16. Solution: The F.B.D. for ABC is shown in Fig. 4.6.16 (a). ΣΜΑ = 0 : - (5) (1) + 10 − (6) (4.5) + (2) (0.67) + (2) (1) + RB (6) = 0 Example 4.6.17 A cylinder weighing 1000 N and 1,5 m diameter is supported by a beam AB of length 6 m and weight 400 N as shown in Fig. 4.6.17. Neglecting friction at the surface of contact of the cylinder, determine, a) Wall reaction at D. b) Tension in cable BC and c) Hinged reaction at support A. Solution : AD and AP are tangents from an external point A. Hence line AO bisects ∠DAP. The free body diagrams of cylinder and beam are as shown Fig. 4.6.17 (b). From F.B.D. of cylinder, From F.B.D. of beam AB : Example 4.6.18 A weight W rests on the bar AB as shown in Fig. 4.6.18. The cable connecting W and B passes over frictionless pulley. If bar AB has negligible weight, show that the reaction at A is W (L-a) /(L+a) Solution: The F.B.D. of block and bar are shown in Fig. 4.6.18 (a). From F.B.D. of block, Example 4.6.19 Rod AB is acted upon by a couple M and two forces, each of magnitude P. Derive an equation relating 0, P, M and l which must be satisfied when the rod is in equilibrium. Refer Fig. 4.6.19. If M = 150 Nm, P = 200 N, and l = 0.6 m, determine θ from the derived equation. Solution: The F.B.D. of rod is shown in Fig. 4.6.19 (a). Note: sin 2θ gives two values of θ between 0 and 90°. They are θ and 90 – θ. Example 4.6.20 For the frame shown in Fig. 4.6.20 determine the reactions at A and B when a) θ = 0° b) θ = 90° and c) θ = 30°. Solution: The F.B.D. of frame is shown in Fig. 4.6.20 (a). a) For θ = 0°, from equation (1), From equation (2), Ax = .0 From equation (3), b) For θ = 90° c) For θ = 30° Example 4.6.21 A loading vehicle is at rest on a track, forming an angle of 30° with the vertical as shown in Fig. 4.6.21. The combined mass of the vehicle with its load is 3500 kg and is acting at the centre of gravity G, which is located halfway between the two axles and 500 mm from the track. Determine the tension in the cable and reactions at front and rear pairs of wheels. Solution: The F.B.D. of vehicle is shown in Fig. 4.6.21 (a) Example 4.6.22 A beam of AF is shown in the Fig. 4.6.22. Find the reactions at A. Solution: The F.B.D. of beam is shown in Fig. 4.6.22 (a). Example 4.6.23 A beam is acted upon by a system of forces as shown in Fig. 4.6.23. Find the support reactions. Solution: The F.B.D. of beam is shown in Fig. 4.6.23 (a). Example 4.6.24 4000 N load acts on the beam held by a cable PQ as shown in Fig. 4.6.24. The weight of the beam can be neglected. Draw the free body diagram of the beam and find the tension in the cable PQ. Also find the reaction force at R. Solution: The free body body diagram of the beam is shown in Fig. 4.6.24 (a). (See Fig. 4.6.24 (a) on next page) Example 4.6.25 A 300 mm wooden beam weighing 540 N is supported by a pin and bracket at A and by cable BC. Find the reaction at A and tension in cable BC, Refer Fig. 4.6.25. Solution: The F.B.D. of beam is shown in Fig. 4.6.25 (a). The angle made by cable with horizontal is, Example 4.6.26 The uniform 18 kg bar OA is held in position as shown in Fig. 4.6.26 by the smooth pin at O and the cable AB. Determine the tension in the cable and the reaction at O. Solution: The angle made by AB with horizontal is, The FBD of bar OA is shown in Fig. 4.6.26 (a) Example 4.6.27 The L-shaped member ACB is supported by a pin support at C and by an inextensible cord attached at A and B and passing over a frictionless pulley at D. Determine the tension in the cord and the reaction at C. Refer Fig. 4.6.27. Solution: The F.B.D. of member ACB is shown in Fig. 4.6.27 (a). Example 4.6.28 Three loads are applied as shown in Fig. 4.6.28 to a light beam supported by cables attached at B and C. Neglecting the weight of the beam, determine the range of values of Q for which neither cable becomes slack when P = 0. Solution: The F.B.D of beam is shown in Fig. 4.6.28 (a).: Example 4.6.29 The boom supports the two vertical loads P1 = 800 N and P2 = 350 N as 'shown in Fig. 4.6.29. Determine the tension in cable BC and component of reaction at A. Solution: The F.B.D. of beam is shown in Fig. 4.6.29 (a). : Example 4.6.30 The wall crane is supported by smooth collar at B and pin at A as shown in Fig. 4.6.30. If the vertical component of reaction at A is 10 kN, determine the force P normal reaction at B and tangential component of reaction at A. Solution: The F.B.D of wall crane is shown in Fig. 4.6.30 (a). Example 4.6.31 Determine the component of reaction at hinge A and tension in the cable BC as shown in Fig. 4.6.31. Solution: The FBD of beam is shown in Fig. 4.6.31 (a). Example 4.6.32 A beam supports a load varying uniformly from an intensity of w1 kN/m at left end to w2 kN/m at the right end as shown in Fig. 4.6.32. If the reactions RL = 6 kN and RR = 12 kN, determine the intensity of loading w1 and w2: Solution: The FBD of beam is shown in Fig. 4.6.32 (a). Example 4.6.33 Determine the length a of overhang so that the reaction at B is twice of the reaction at A for the beam loaded and supported as shown in Fig. 4.6.33. Solution: Draw FBD of beam as shown in Fig. 4.6.33 (a). Replace the udl from A to B by a point load of 20 kN at 1 m from A and udl from B to C by point load of 10 a at distance a/2 to the right of B. Example 4.6.34 A fixed crane has a mass of 1000 kg and is used to lift a 2400 kg crate as shown in Fig. 4.6.34. It is held in place by a pin at A and a rocker at B. The center of gravity of the crane is located at G. Determine the reactions at supports, A and B. Solution: The F.B.D. of crane is shown in Fig. 4.6.34(a) Example 4.6.35 The frame (Fig. 4.6.35) supports the part of the roof of a small building. The tension in the cable is 150 kN. Determine the reaction at the fixed end E. The F.B.D. of frame is shown in Fig. 4.6.35(a) From Fig. 4.6.35 (a), Example 4.6.36 A light bar AD is suspended from a cable BE and supports a 50 kg block at C as shown in Fig. 4.6.36. The ends. A and D of the bar in contact with frictionless vertical walls. Determine the tension in cable BE and the reactions at A and D. Solution: The F.B.D. of bar is shown in Fig. 4.6.36 (a) Example 4.6.37 Find the pin reaction of A and the roller reaction at B. For the beam shown in Fig. 4.6.37. Solution: The F.B.D. of beam is shown in Fig. 4.6.37(a). Example 4.6.38 Find the reaction at A and B for the beam loaded as shown in Fig. 4.6.38. Solution: i) The F.B.D. of beam is shown in Fig. 4.6.38(a). ii) The F.B.D of beam is shown in Fig. 4.6.38 (b). Example 4.6.39 Determine the tension in cable BC as shown in Fig. 4.6.39. Neglect the self weight of AB. Solution: The free body diagram of the beam is shown in Fig. 4.6.39(a). Example 4.6.40 A 50 kg crate Fig. 4.6.40 is attached to the trolley-beam system shown. Knowing that α = 1.5 m, determine (i) the tension in cable CD, (ii) the reaction at B? Solution: The FBD of beam AB is shown in Fig. 4.6.40 (a). Example 4.6.41 Block P = 5 kg and block Q of mass m kg is suspended through the chord is in the equilibrium position as shown in Fig. 4.6.41. Determine the mass of block Q. Solution: The free body diagrams of points B and C are shown in Fig. 4.6.41 (a). Using Lami's theorem for B, ⸫ TBC = 29.643 N Using Lami's theorem for C, Example 4.6.42 A light string ABCDE whose extremity A is fixed, has waghts W1 and W 2 attached to it at B and C. It passes round a small smooth peg at D carrying a weight of 300 N at the free end E as shown in Fig. 4.6.42. If in the equilibrium position, BC is horizontal and AB and CD make 150° and 120° with BC, find (i) Tensions in the portion AB, BC and CD of the string and (ii) Magnitudes of W1 and W2. Solution: For the F.B.D. of joint C shown in Fig. 4.6.42 (a). As the peg at D is smooth, the tension in CD is same as that of load i.e. TCD = 300 N. Applying Lami's theorem, Similarly for the F.B.D. of joint B shown in Fig. 4.6.42 (b). Applying lami's theorem, Example 4.6.43 Three links PQ, QR and RS connected as shown in Fig. 4.6.43 support loads W and 50 N. Find the weight W and the force in each link if the system remains in equilibrium. Solution: For the F.B.D. of point Q shown in Fig. 4.6.43 (a), For the F.B.D. of point R shown in Fig. 4.6.43 (b). As per Lami's theorem Example 4.6.44 Find the support reactions of the truss loaded as shown in Fig. 4.6.44. Solution: The F.B.D.of truss is shown in Fig. 4.6.44 (a). Example 4.6.44 A rope AB, 4.5 m long is connected at two points A and B at the same level 4 m apart. A load of 1500 N is suspended from a point C on the rope 1.5 m from A as shown in Fig. 4.6.45 (b). What load connected at a point D on the rope. 1 m from B will be necessary to keep the position CD level? Solution : Total length ACDB = AC + CD + DB = 1.5 + 2 + 1 = 4.5 m l(CD) = l (EF) = 2 m AB = 4 m … (Given) But, AB = 4 = AE + EF + FB AB = 4 = x + 2 + FB ⸫ FB = 4 - x − 2 = 2 − x Consider Δ FBD, (BD)2 (FB)2 + (FD)2 12 = (2 - x)2 + y2 … (1) Consider Δ AEC, (AC)2 = (AE)2 + (EC)2 1.52 = x2 + y2 ⸫ y2 = 1.52 - x2 Put this value in equation (1), Considering FBD of points C and D, Applying Lami's theorem on Fig. 4.6.45 (a) and (b). Example 4.6.46 Determine the reactions at A and B of the over-hanging beam shown in Fig. 4.6.46 (b). Solution : Applying equilibrium conditions, Examples for Practice Q.1 An axial force F = 6 kN, moment M 8 kN-m and unknown forces P, Q and R acting on a body AC 6 m long, keep it in equilibrium as shown in Fig. 4.6.47. Determine unknown forces P, Q and R. [Ans. : P = 5.2 kN, Q = 3.6 kN, R = 2 kN] Q.2 Beam AB shown in Fig. 4.6.48 has hinged support at A and roller support at B.. Determine the reactions developed at the support when the forces shown in the figure are acting. Q.3 A beam ABCDEF is hinged at A and supported on rollers at E and carries loads as shown in Fig. 4.6.49. Determine the reactions at supports. Q.4 Determine the reactions at the ends of the beams AB and CD as shown in Fig. 4.6.50. Neglect the self weight of the beams. Q.5 A man raises a 10 kg joist of 4 m length by pulling on a rope attached to the joist as shown. At this instant, find tension in the rope and reaction at end A of joist. Refer Fig. 4.6.51. [Ans. : T = 82.07 N, RA = 147.87 N, 58.57°] Q.6 A boom AC hinged at A supports a 400 N load as shown in Fig. 4.6.52. Find the force in cable BC, which is attached to the wall at B. Neglect self weight of boom. [Ans. : TBC = 292.82 N] Q.7 Assuming pulley to be smooth, calculate support reactions for beam AD as shown in Fig. 4.6.53. [Ans. : RA = 68.54 kN, 78.1o Q.8 Determine the reactions at the supports for the beam loaded as shown in Fig. 4.6.54.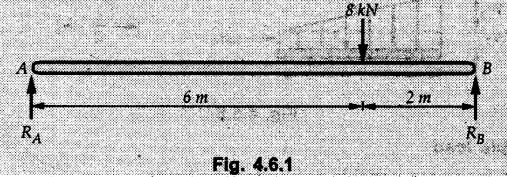


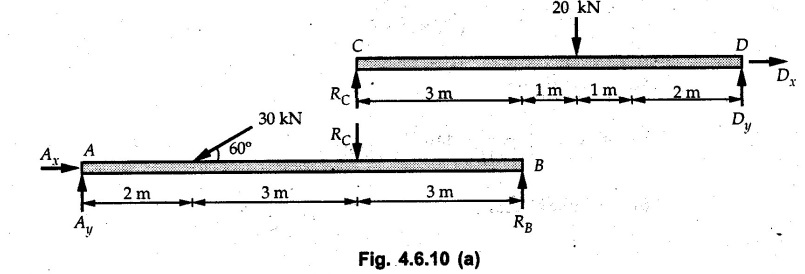 For CD,
For CD,




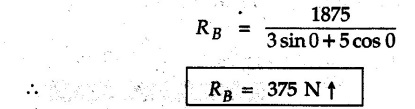
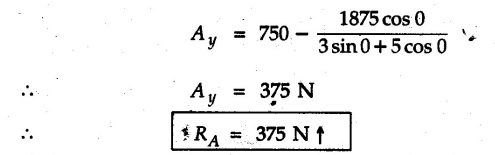



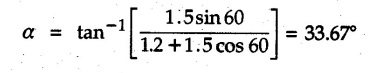
 Solution:
Solution: 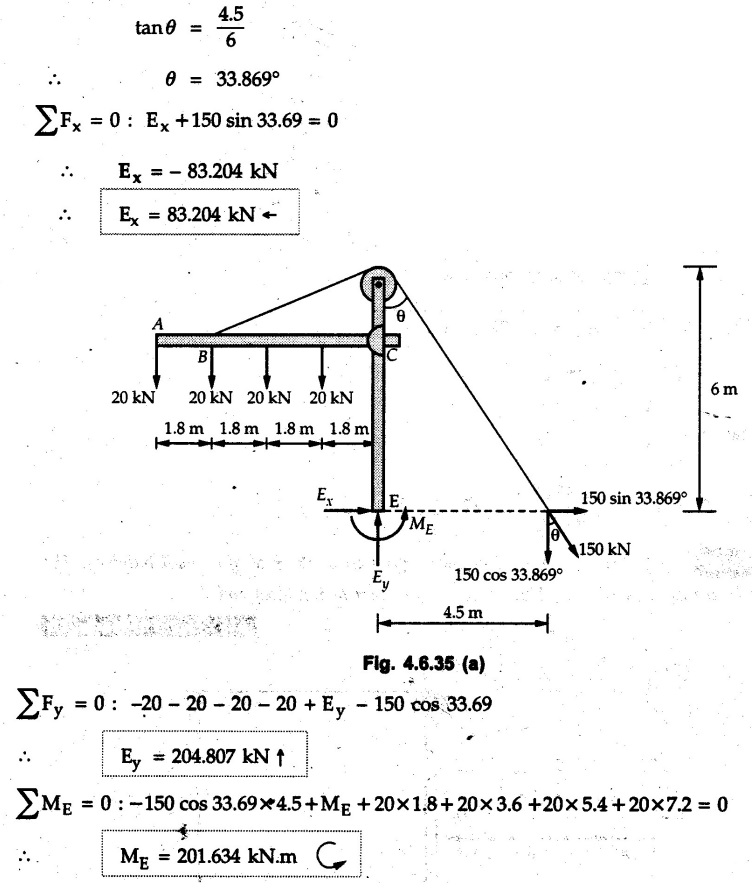



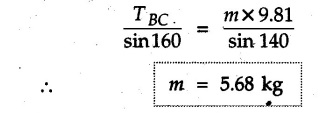

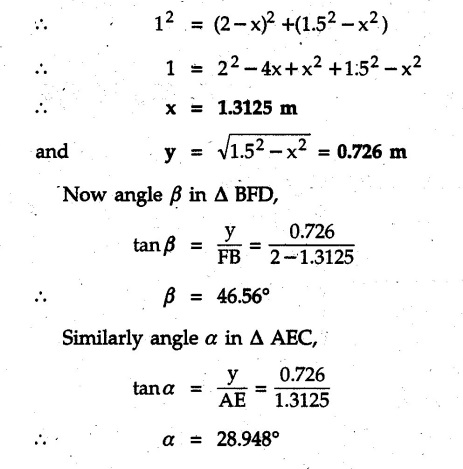



 RC = 98.79 kN ↑]
RC = 98.79 kN ↑]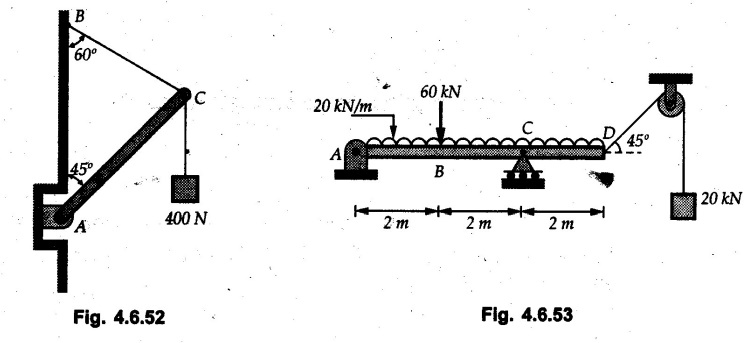
Engineering Mechanics: Unit II: Equilibrium of Rigid Bodies : Tag: : - Solved Example & Practice Problems: Equilibrium of Coplanar Non-Concurrent Force System
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
