Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Solved Anna University Problems on Thermodynamic Relations
Solved Anna University Problems on Thermodynamic Relations: Gas Mixtures and Thermodynamic Relations - Engineering Thermodynamics
SOLVED ANNA UNIVERSITY PROBLEMS ON THERMODYNAMIC RELATIONS AU Problem 5.1 Consider an ideal gas at 303 K and 0.86 m3/kg. As a result of some disturbance the state of the gas changes to 304 K and 0.87 m3/kg. Estimate the change in pressure of the gas as the result of this disturbance. Given data: T1 = 303 K v1 = 0.86 m3/kg T2 = 304 K v2 = 0.87 m3/kg Solution: AU Problem 5.2 A vessel of volume 0.3 m3 contains 15 kg of air at 303 K. Determine the pressure exerted by the air using, (1) perfect gas equation (2) Van der Waals equation. Take critical temperature of air as 132.8 K. Critical pressure of air is 37.7 bar. Same as Problem 5.1 on Page 5.23. AU Problem 5.3 One kmol of methane is stored in a rigid vessel of volume 0.6 m3 at 20°C. Determine the pressure developed by the gas by making use of the compressibility chart. Given data: m = 1 kmol T = 20°C = 20 + 273 = 293 K V = 0.6 m3 Solution: AU Problem 5.4 A vessel of volume of 0.28 m3 contains 10 kg of air at 320 K. Determine the pressure exerted by the air using (a) perfect gas equation (b) Van der walls equation (c) Generalised compressibility chart. (Take critical temperature of air as 132.8 K and critical pressure of air as 37.7 bar. Similar to Problem 5.1 on Page 5.23. [Ans:- (i) p = 3085.71 kPa by perfect gas equation (ii) p = 3227.92 kPa by Van der Waals equation (iii) p = 3247.2 kPa by generalised compressibility chart.] AU Problem 5.5 Determine the pressure of nitrogen gas at T = 175 K and v = 0.00375m3/kg on the basis of the (i) ideal gas equation of state (ii) Van der Waals equation of state. The Van der Waals constants for nitrogen are a = 0.175 m6kPa/kg2, b = 0.00138 m3/kg. Similar to Problem 5.1 on Page 5.23. [Ans:- (a) 13, 860 kPa and (b) 9468 kPa] AU Problem 5.6 One kg of CO2 has volume of 1 m3 at 100°C. Compute the pressure by (1) Van der Waals equation (2) Perfect gas equation. The Van der Waals constants a = 362850 Nm4/(kmol)2 and b = 0.0423 m3/(kmol). Given data: Mass, m = 1 kg Volume, V = 1 m3 Temperature, T = 100°C = 273 + 100 = 373 K a = 362850 Nm4/(kmol)2 b = 0.0423 m3/(kmol) Solution: 1. Van der Waals equation: Molar mass of CO2, M = 12 + 16 × 2 = 44 kg/kmol 2. Perfect gas equation: AU Problem 5.8 A certain gas has Cp = 0.913 kJ/kgK and Cv = 0.653 kJ/kgK. Find the molecular weight and specific gas constant R of the gas. Given data: Cp = 0.913 kJ/kgK Cv = 0.653 kJ/kgK Solution: Gas constant, R = Cp - Cv AU Problem 5.9 Using the ideal-gas equation of state, verify (1) the cycle relation, and (2) the reciprocity relation at constant p. Solution: (1) The cycle relation: Based on the theorem 3 of exact differential, the relation between pressure, volume and temperature is given by (2) The reciprocity relation at constant P: The reciprocity rule of ideal gas p = constant It can be expressed by AU Problem 5.10 Derive expressions Solution: AU Problem 5.11 Two moles of an ideal gas at temperature 'T' and pressure 'p' are contained in a compartment. An adjacent compartment contains one mole of an ideal gas at temperature '2T' and pressure 'p'. The gases mix adiabatically but do not react chemically when a partition separating the component is withdrawn and the temperature of the mixture is (4/3)T'. Show that the entropy increase due to the mixing process is given by Assume that the gases are different and the ratio of specific heat 'γ' is the same for both gases and remains constant. Given data: n1 = 2 moles n2 = 1 mole T1 = T T2 = 2T Tm = (4/3)T Solution: Mole fraction of gas 1, y1 = 2/3 AU Problem 5.12 Show that for a gas that obeys the law p(v - b) = RT, a Joule-Thomson expansion from pressure pi to p2 produces a temperature change which can be found from the solution of Solution: p(v - b) = RT It can be rewritten as AU Problem 5.13 Verify the validity of Maxwell's relation, Given data: T = 300°C = 300 + 273 = 573 K p = 500 kPa Solution: Consider the interval 40°C for temperature and 40 kPa for pressure, AU Problem 5.14 One kg of ideal gas is heated from 50°C to 150°C. If R = 280 J/kg K and γ = 1.32 for the gas, determine: (1) Cp and Cv (2) Change in internal energy, (3) Change in enthalpy, (4) Change in flow energy. Given data: Initial temperature, T1 = 50°C = 50 + 273 = 323 K Final temperature, T2 = 150°C = 150 + 273 = 423 K Gas constant, R = 280 J/kgK = 0.28 kJ/kgK γ = 1.32 Solution: AU Problem 5.15 The latent heat of vaporization at 1 bar pressure is 2258 kJ/kg and the saturation temperature is 99.4°C. Calculate the saturation temperature at 2 bar pressure using Clausius-Clapeyron equation. Verify the same from the steam table data. Given data: Pressure, p1 = 1 bar Latent heat, hfg = 2258 kJ/kg Saturation temperature, Ts = 99.4°C = 273 + 99.4 = 372.4 K Pressure, p2 = 2 bar Solution: The individual gas constant for water vapor, R = 0.4615 kJ/kgK Using the following Clausius-Clapeyron equation (5.105), AU Problem 5.16 A vessel of capacity 3 m3 contains 1 kg mole of N2 at 90°C. (i) Calculate pressure and the specific volume of the gas. (ii) If the ratio of specific heats is 1.4, evaluate the values of Cp and Cv (iii) Subsequently, the gas cools to the atmospheric temperature of 20°C, then evaluate the final pressure of gas. (iv) Evaluate the increase in specific internal energy, the increase in specific enthalpy, increase in specific entropy and magnitude and sign of heat transfer. Given data: Mass of N2, m = 1 kg mole = 28 kg Volume, V1 = 3 m3 Initial temperature, T1 = 90°C = 90 + 273 = 363 K Final temperature, T2 = 20°C = 20 + 273 = 293 K γ = 1.4 Solution: AU Problem 5.17 CO2 flows at a pressure of 10 bar and 180°C into a turbine, located in a chemical plant, and there it expands reversibly and adiabatically to a final pressure of 1.05 bar. Calculate the final specific volume, temperature and increase in entropy. Neglect changes in velocity and elevation. If the mass flow is 6.5 kg/min, evaluate the heat transfer rate from the gas and the power delivered by the turbine. Assume CO2 to be a perfect gas and Cv = 0.837 kJ/kgK. Given data: p1 = 10 bar = 1000 kN/m2 T1 = 180°C = 180 + 273 = 453 K p2 = 1.05 bar = 105 kN/m2 mf = 6.5 kg/min = 0.1083 kg/s Cv = 0.837 kJ/kgK Solution: Given that, Cv = 0.837 kJ/kgK Molecular weight of CO2, M = 44 Q = 0 Ans. From SFEE of turbine (i.e. changes in velocity & elevation are negligible, & Q = 0) W = mf (h1 - h2) = mf Cp (T1 - T2) = 0.1083 × 1.0259 (453 - 297.2) = -17.3 kJ/s or kW Ans.

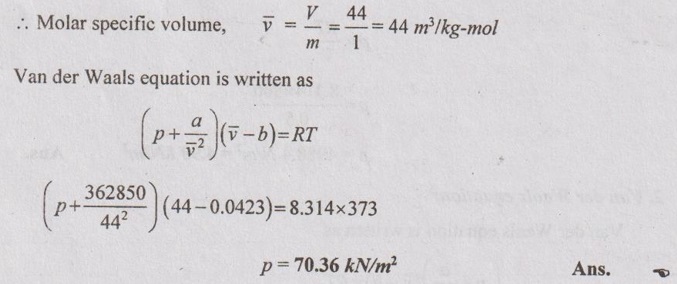
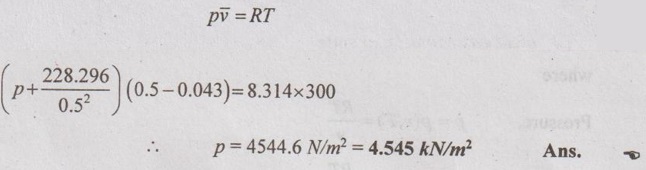
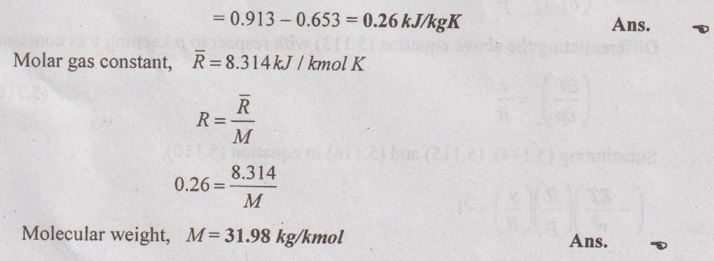


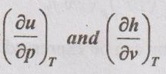 in terms of p, v and T only.
in terms of p, v and T only.
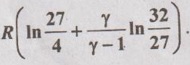
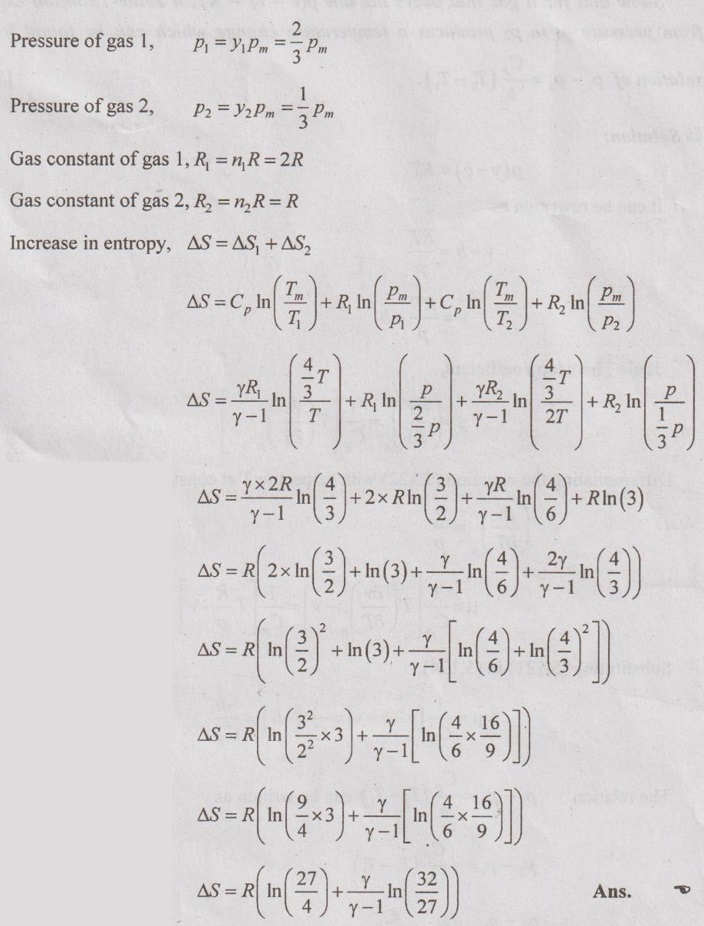 Hence, it is proved.
Hence, it is proved.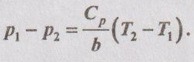

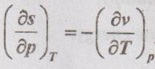 for steam at 300°C and 500kPa.
for steam at 300°C and 500kPa.
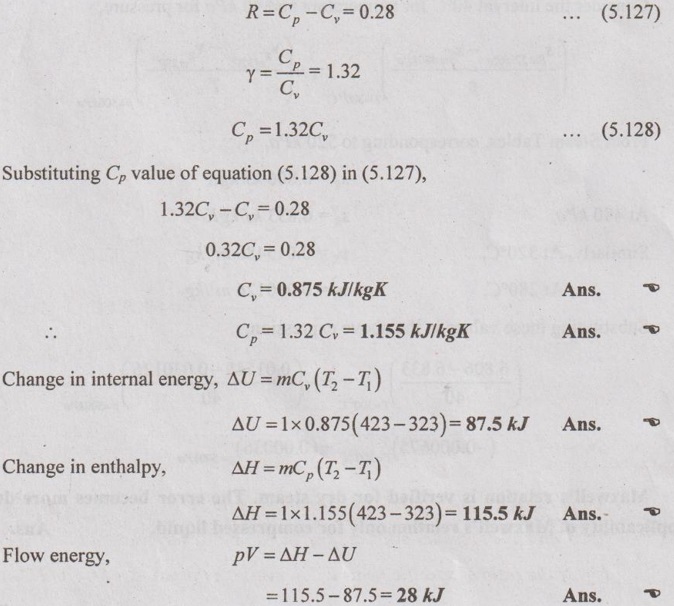


 Similarly, for adiabatic process, heat transfer rate,
Similarly, for adiabatic process, heat transfer rate,

Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : - Solved Anna University Problems on Thermodynamic Relations
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
