Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Solved Anna University Problems on Gas Mixtures
Gas Mixtures and Thermodynamic Relations | Engineering Thermodynamics
Solved Anna University Problems on Gas Mixtures: Gas Mixtures and Thermodynamic Relations - Engineering Thermodynamics
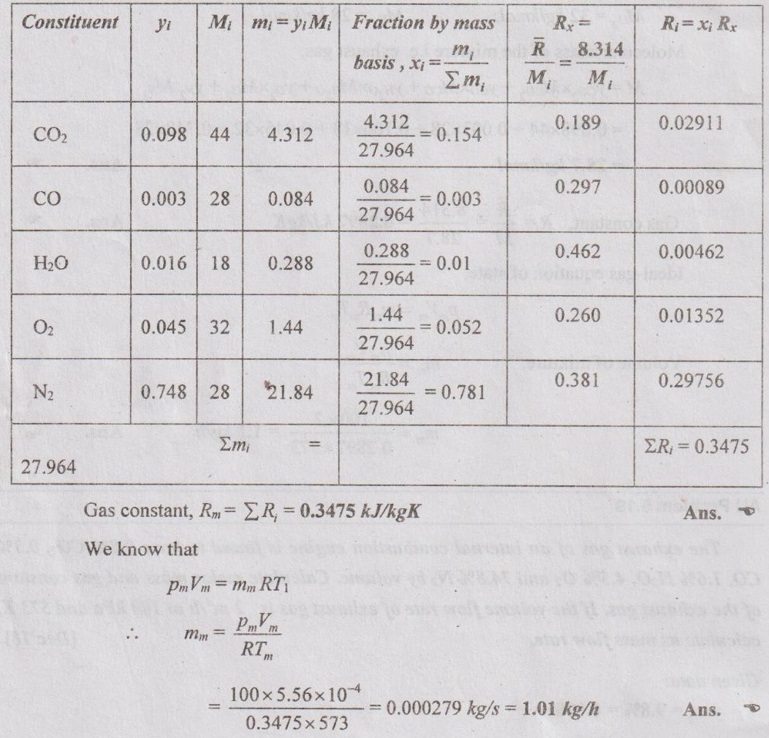
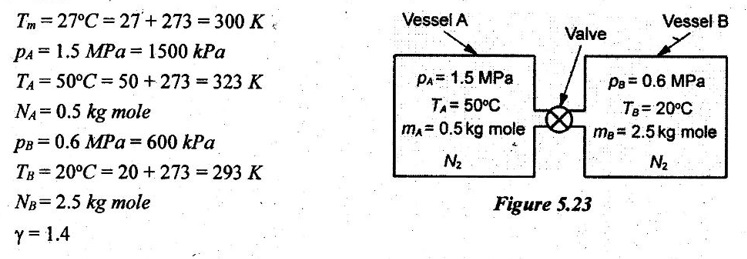
SOLVED ANNA UNIVERSITY PROBLEMS ON GAS MIXTURES AU Problem 5.18 The exhaust gas of an internal combustion engine is found to have 9.8% CO2, 0.3% CO, 10.6% H2O, 4.5% O2 and 74.8% N2 by volume. Calculate molar mass and gas constant of the exhaust gas. If the volume flow rate of exhaust gas is 2 m3/h at 100 kPa and 573 K, calculate its mass flow rate. Given data: yco2 = 9.8% = 0.098 yco = 0.3% = 0.003 yн2O =10.6% = 0.106 yO2 = 4.5% = 0.045 yN2 = 74.8% = 0.748 vm = 2 m3/h pm = 100 kPa Tm = 573 K Solution: Molecular masses of given constituents of exhaust gas are, AU Problem 5.19 The exhaust gas of an internal combustion engine is found to have 9.8% CO2, 0.3% CO, 1.6% H2O, 4.5% O2 and 74.8% N2 by volume. Calculate molar mass and gas constant of the exhaust gas. If the volume flow rate of exhaust gas is 2 m3/h at 100 kPa and 573 K, calculate its mass flow rate. Given data: yco2 = 9.8% = 0.098 yco = 0.3% = 0.003 yн2O = 1.6% = 0.016 yO2 = 4.5% = 0.045 yN2 = 74.8% 0.748 Tm = 573 K Vm = 2 m3/h = 2/3600 = 5.56 × 10-4 m3/s pm = 100 kPa Solution: The given analysis is converted from volumetric basis to mass basis. AU Problem 5.20 A rigid tank contains 2 kmol of N2 and 6 kmol of CO2 gases at 300 K and 15 MPa. Estimate the volume of the tank on the basis of (1) The ideal-gas equation of state, (2) Compressibility factors and Amagat's law and (3) Compressibility factors and Dalton's law. Given data: NN2 = 2 kmol Nco2 = 6 kmol Tm = 300 K pm = 15 MPa = 15000 kPa Solution: Total number of moles of mixture, Nm = NN2 + Nco2 = 2 + 6 = 8 kmol (i) By ideal-gas equation of state method: Ideal-gas equation of state, (ii) By Compressibility factors and Amagat's law: The pseudo critical temperature and pseudo critical pressure of the mixture by using the critical-point properties of N2 and CO2 table. (iii) By compressibility factors and Dalton's law: The volume of mixture is assumed to be the same as ideal gas equation volume. AU Problem 5.21 A mixture of ideal gases consists of 3 kg of nitrogen and 5 kg of carbon dioxide at a pressure of 300 kPa and a temperature of 20°C, find the: (i) Mole fraction of each constituent (ii) Equivalent molecular weight of the mixture (iii) Equivalent gas constant of the mixture (iv) Partial pressures and the partial volumes. Given data: mN2 = 3 kg mco2 = 5 kg pm = 300 kPa Tm = 20°C = 20 + 273 = 293 K Solution: AU Problem 5.22 0.45 kg of CO2 and 1 kg of air is contained in a vessel of volume 0.4 m3 at 15°C. Air has 23.3% of O2 and 76.7% of N2 by mass. Calculate the partial pressure of each constituent and total pressure in the vessel. Molar masses of CO, O2 and N2 are 28, 32 and 28 kg/kmol. Given data: mco = 0.45 kg mair = 1 kg Vm = 0.4 m3 Tm = 15°C = 15 + 273 = 288 K xo2 = 0.233 xN2 = 0.767 MCO = 28 kg/kmol MO2 = 32 kg/kmol MN2 = 28 kg/kmol Solution: AU Problem 5.23 A closed vessel has a capacity of 0.5 m3. It contains 20% nitrogen and 20% oxygen 60% carbon dioxide by volume at 20°C and 1 MPa. Calculate the molecular mass, gas constant, mass percentages and mass of mixture. Given data: vm = 0.5 m3 yN2 = 20% = 0.2 yO2 = 20% = 0.2 yco2 = 60% = 0.6 Tm = 20°C = 20 + 273 = 293 K pm = 1 MPa = 1000 kPa Solution: AU Problem 5.24 A closed vessel has a capacity of 500 litres. It contains 20% nitrogen and 20% oxygen, 60% carbon di-oxide by volume at 100°C and 1 MPa. Calculate the molecular mass, gas constant, mass percentages and the mass of mixture. Same as AU Problem 5.23 on Page 5.113. AU Problem 5.25 Atmospheric air at 101.325 kPa and 288.15 K contains 21% oxygen and 79% nitrogen, by volume. Calculate the (i) Mole fractions, mass fractions and partial pressures of oxygen and nitrogen and (ii) Molar mass, gas constant and density of the air. Take molar mass of oxygen and nitrogen as 32 kg/kmol and 28 kg/kmol. Given data: pa = 101.325 kPa Ta = 288.15 K yo2 = 21% yN2 = 79% MO2 = 32 kg/kmol MN2 = 28 kg/kmol Solution: AU Problem 5.26 A mixture of ideal gases consists of 2.5 kg of N2 and 4.5 kg of CO2 at a pressure of 4 bar and a temperature of 25°C. Determine: (1) Mole fraction of each constituent, (2) Equivalent molecular weight of the mixture, (3) Equivalent gas constant of the mixture, (4) The partial pressure and partial volumes, (5) The volume and density of the mixture. Similar to AU Problem 5.23 on Page 5.113. AU Problem 5.27 A mixture of hydrogen (H2) and Oxygen (O2) is to be made so that the ratio of H2 to O2 is 2:1 by volume. If the pressure and temperature are 1 bar and 25°C respectively, calculate the: (i) mass of O2 required and (ii) volume of the container. Given data: Pressure, pm = 1 bar = 100 kPa Temperature, Tm = 25°C = 25 + 273 = 298 K Solution: AU Problem 5.28 A mixture of 2 kg oxygen and 2 kg Argon is in an insulated piston cylinder arrangement at 100 kPa, 300 K. The piston now compresses the mixture to half its initial volume. Molecular weight of oxygen is 32 and for argon it is 40. Ratio of specific heats for oxygen is 1.39 and for argon is 1.667. Calculate the pressure and temperature after compression and also find the work done on the piston. Given data: Solution: AU Problem 5.29 An insulated rigid tank is divided into two compartments by a partition. One compartment contains 7 kg of oxygen gas at 40°C and 100 kPa, and the other compartment contains 4 kg of nitrogen gas at 20°C and 150 kPa. Now, the partition is removed and the two gases are allowed to mix. Determine the (1) mixture temperature and (2) mixture pressure after equilibrium has been established. Given data: Solution: AU Problem 5.30 A perfect gas mixture consists of 4 kg of N2 and 6 kg of CO2 at a pressure of 4 bar and a temperature of 25°C. For N2: Cv = 0.745 kJ/kgK and Cp = 1.041 kJ/kgK. For CO2: Cv = 0.653 kJ/kgK and Cp = 0.842 kJ/kgK. Find Cp, Cv and R of the mixture. If the mixture is heated at constant volume to 50°C, find the changes in internal energy, enthalpy and entropy of the mixture. Given data: Solution: AU Problem 5.31 A mixture of 3 moles of helium, 4 moles of neon and 5 moles of argon is at 1 bar and 300 K. Calculate the (1) volume, (2) mole fraction and partial pressure of gases and (3) change of entropy due to mixing. Given data: NHe = 3 NNe = 4 NAr = 5 pm = 1 bar = 100 kPa Tm = 300 K Solution: From gas properties table, the values of atomic mass or molecular weight are taken. Molecular weight of helium, MHe = 4 kg/kmol Molecular weight of argon, MAr = 40 kg/kmol Molecular weight of neon, MNe = 20 kg/kmol AU Problem 5.32 A gas mixture consists of 7 kg nitrogen and 2 kg oxygen at 4 bar and 27°C. Calculate the mole fraction, partial pressures, molar mass, gas constant, volume and density. Given data: mN2 = 7 kg mO2 = 2 kg pm = 4 bar Tm = 27°C Hint: Molecular weight of oxygen = 32 kg/kmol (⸪ O = 16; O2 = 32) Molecular weight of nitrogen = 28 kg/kmol (⸪ N = 14; N2 = 28) Solution: AU Problem 5.33 In an engine cylinder, a gas has a volumetric analysis of 13% CO2, 12.5% O2 and 74.5% N2. The temperature at the beginning of expansion is 950°C and the gas mixture expands reversibly through a volume ratio of 8:1, according to the law pV1.2 = constant. Calculate per kg of gas: (i) Work done (ii) Heat flow (iii) Change of entropy per kg of mixture. The values of Cp for the constituents CO2, O2 and N2 are 1.235 kJ/kgK, 1.088 kJ/kgK and 1.172 kJ/kgK respectively. Given data: Solution: The given analysis is converted from volumetric basis to mass basis. AU Problem 5.34 A rigid tank of 5 m3 contains gas mixture comprising 3 kg of O2, 4 kg of N2 and 5 kg of CO2 at 290 K. Calculate the molar specific volume and initial pressure of the gas. If it is heated to 350 K, calculate the heat transfer and change in enthalpy. Also verify the Gibbs theorem for entropy. Given data: V = 5 m3 T1 = 290 K mO2 = 3 kg MN2 = 4 kg mCO2 = 5 kg T2 = 350 K Solution: Equivalent molecular weight of the mixture, AU Problem 5.35 A rigid tank that contains 2 kg of N2 at 25°C and 550 kPa is connected to another rigid tank that contains 4 kg of O2 at 25°C and 150 kPa. The valve connecting the two tanks is opened and the two gases are allowed to mix. If the final mixture temperature is 25°C, determine the volume of each tank and the final mixture pressure. Given data: Solution: AU Problem 5.36 Two vessels, A and B, both containing nitrogen, are connected by a valve which is opened to allow the contents to mix and achieve an equilibrium temperature of 27°C. Before mixing in vessel A has pressure 1.5 MPa, temperature 50°C, contents 0.5 kg mole and vessel B has pressure 0.6 MPa, temperature 20°C, contents 2.5 kg mole. Compute the final equilibrium pressure, and the amount of heat transferred to the surroundings. If the vessel is perfectly insulated, calculate the final temperature and pressure which would have been reached. Take γ = 1.4. Given data: Solution: Measuring the internal energy above the datum of absolute zero i.e. at T = 0 K & u = 0 kJ/kg. Internal energy U1 (before mixing) = mACvTA + mBCvTB = 14 × 0.7425 × 323 + 70 × 0.7425 × 293 = 18586.26 kJ Internal energy U2 (after mixing), = mm Cv Tm = 84 × 0.7425 × 300 = 18711 kJ
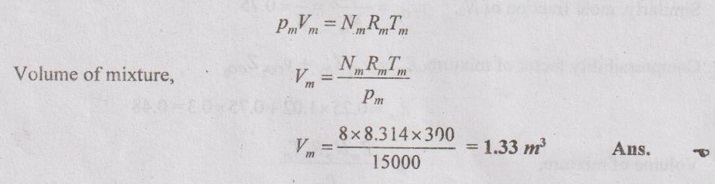





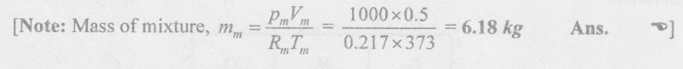

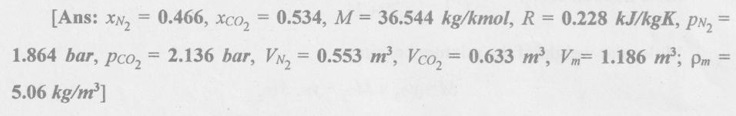




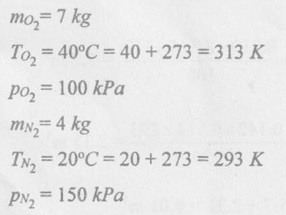



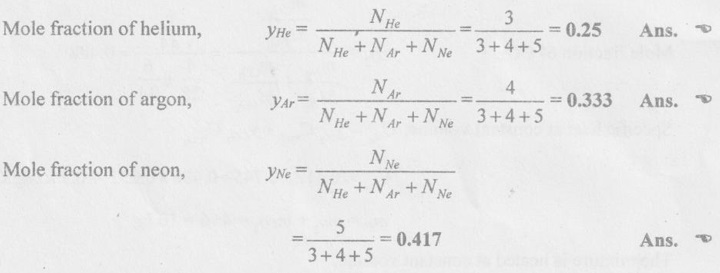
 Since Tm = THe = TAr = TNe the above equation becomes,
Since Tm = THe = TAr = TNe the above equation becomes,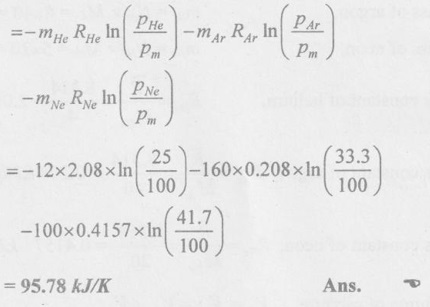





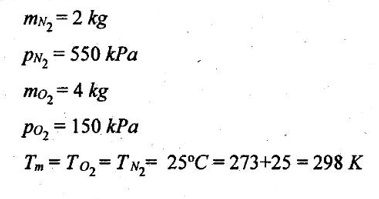


Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : Gas Mixtures and Thermodynamic Relations | Engineering Thermodynamics - Solved Anna University Problems on Gas Mixtures
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
