Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Solved Anna University Problems on Entropy principles
Thermodynamics
Solved Anna University Problems on Entropy principles: Availability and Applications of II Law - Engineering Thermodynamics
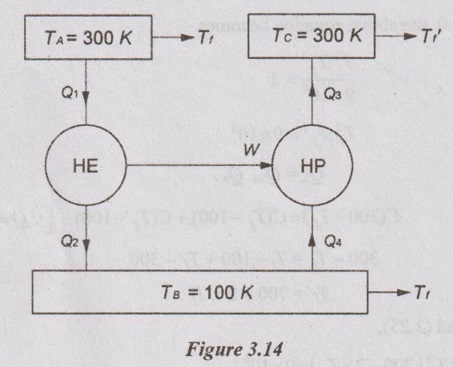
SOLVED ANNA UNIVERSITY PROBLEMS ON ENTROPY PRINCIPLES AU Problem 3.1 Air in a closed vessel of fixed volume 0.15 m3 exerts pressure of 12 bar at 250°C. If the vessel is cooled so that the pressure falls to 3.5 bar, determine the final temperature, heat transfer and change of entropy. Given data: V1 = 0.15 m3 p1 = 12 bar = 1200 kN/m2 T1 = 250°C = 273 + 250 = 523 K p2 = 3.5 bar = 350 kN/m2 To find: T2, Q and ΔS Solution: From ideal gas equation, For constant volume process, Heat transfer, Q = mCv (T2 - T1) (Negative sign indicates that the heat is rejected from the system) AU Problem 3.2 A certain gas has Cp =1.968 kJ/kgK and C, = 1.507 kJ/kgK. Find its molecular weight and the gas constant. A constant volume chamber of 0.3 m3 capacity contains 2 kg of this gas at 5°C. Heat is transferred to the gas until the temperature is 100°C. Find the work done, the heat transferred and the change in internal energy, enthalpy and entropy. Given data: Cp = 1.968 kJ/kgK C = 1.507 kJ/kgK V1 = 0.3 m3 For constant volume process, V2 = V1 = 0.3 m3 m = 2 kg T1 = 5°C = 5 + 273 = 278 K T2 = 100°C = 100 + 273 = 373 K Solution: AU Problem 3.3 In an isothermal process 1000 kJ of work is done by the system at a temperature of 200°C. What is the entropy change of the process? Given data: Work done, W = 1000 kJ Temperature, T = 250°C = 250 + 273 = 473 K Solution: For isothermal process, work done = Heat transfer AU Problem 3.4 A fluid undergoes a reversible adiabatic compression from 4 bar, 0.3 m3 to 0.08 m3 according to the law pV1.25 = C. Determine the change in enthalpy, change in internal energy and change in entropy. Given data: p1 = 4 bar 400 kPa V1 = 0.3 m3 V2 = 0.08 m3 Solution: According to the law, pV1.25 = C We know that for adiabatic process, Heat transfer, Q = 0 From first law of thermodynamics, Q = W + ΔU 0 = -187.96 + ΔU AU Problem 3.5 5 kg of air at 2 bar and 30°C is compressed to 24 bar pressure according to the law pv1.2 = constant. After compression air is cooled at constant volume to 30°C. Determine the (i) volume and temperature at the end of compression, (ii) change of entropy during compression and (iii) change in entropy during constant volume cooling. Take Cp = 1.005 kJ/kg K, Cv = 0.718 kJ/kg K. Given data: m = 5 kg p1 = 2 bar = 200 kPa T1 = 30°C = 30 + 273 = 303 K p2 = 24 bar = 2400 kPa pV1.2 = constant T3 = 30°C = 30 + 273 = 303 K Cp = 1.005 kJ/kg K Cv = 0.718 kJ/kg K To find: V2, T2, S2 - S1 and S3 - S2 Solution: According to the law, pv1.2 = C ⸫ p1V11.2 = p2V21.2 From characteristic gas equation, pV = mRT Similarly, Change in entropy during compression, AU Problem 3.6 0.2 kg of air at 1.5 bar and 27° C is compressed to a pressure of 15 bar according to the law pv1.25 Constant. Determine the work done on or by air, heat flow to or from the air and increase or decrease in entropy. Given data: m = 0.2kg p1 = 1.5 bar = 150 kPa T1 = 27°C = 27 + 273 = 300 K p2 = 15 bar = 1500 kPa pV1.25 = C To find: W, Qs and ΔS Solution: By general gas equation, p1V1 = mRT1 AU Problem 3.7 In a closed system, air is at a pressure of 1 bar, temperature of 300 K and volume of 0.025 m3. The system executes the following processes during the completion of thermodynamic cycle: 1-2; constant volume heat addition till pressure reaches 3.8 bar, 2-3; constant pressure cooling of air, 3-1; isothermal heating to initial state. Determine the change in entropy in each process. Take Cv = 0.718 kJ/kgK, R = 287 J/kgK. Given data: p1 = 1 bar = 100 kPa T1 = 300 K V1 = V2 = 0.025 m3 1-2; constant volume heat addition till pressure reaches p2 = 3.8 bar = 380 kPa 2-3; constant pressure cooling, p2 = p3 3-1; isothermal heating to initial state, T3 = T1 = 300 K Cv = 0.718 kJ/kgK R = 287 J/kgK = 0.287 kJ/kgK Solution: From ideal gas equation, Process 1-2: Constant volume Change in entropy during constant volume process, Process 2-3: Constant pressure cooling Process 3-1: Constant temperature process AU Problem 3.8 5 m3 of air at 2 bar, 27°C is compressed up to 6 bar pressure following pV1.3 constant. It is subsequently expanded adiabatically to 2 bar. Considering the two processes to be reversible, determine the network, net heat transfer and change in entropy. Also plot the processes on T-s and p-V diagrams. Given data: V1 = 5 m3 P1 = 2 bar = 200 kN/m2 T1 = 27°C = 27 + 273 = 300 K P2 = 6 bar = 600 kN/m2 pV1.3 = C ⸫ n = 1.3 Process 1-2: Polytropic Process 2-3: Reversible adiabatic p3 = 2 bar = 200 kN/m2 To find: W, Q, ΔS and T-s and p-V diagrams Solution: Process 1-2: Polytropic process From general gas equation, p1V1 = mRT1 From polytropic process relation, Process 2-3: Adiabatic process From adiabatic process relation, AU Problem 3.9 A mass of air is initially at 260°C and 700 kPa and occupies 0.028 m3. The air is expanded at constant pressure to 0.084 m3. A polytropic process with n = 1.5 is then carried out, followed by a constant temperature process. All the processes are reversible. 1. Sketch the cycle in p - V and T-s planes. 2. Find the heat received and heat rejected in the cycle. 3. Find the efficiency of the cycle. Given data: T1 = 260°C = 273 + 260 = 533 K p1 = 700 kPa = p2 V1 = 0.028 m3 V2 = 0.084 m3 Process 1-2 is constant pressure Process 2-3 is polytropic Process 3-1 is constant temperature To find: Sketch p-V and T-s diagram, Q and η Solution: Process 1-2: Constant pressure process Process 2-3: Polytropic process For polytropic process, Process 3-1: Constant temperature process T1 = T3 = 260°C = 533 K for constant temperature process AU Problem 3.10 A quantity of air undergoes a thermodynamic cycle consisting of three processes. Process 1-2: Constant volume heating from p1 = 0.1 MPa, T1 = 15°C, V1 = 0.02 m3 to p2 = 0.42 MPa. Process 2-3: Constant pressure cooling. Process 3-1: Isothermal heating to the initial state. Employing the ideal gas model with Cp = 1 kJ/kgK, evaluate the change of entropy for each process. Sketch the cycle on p-V and T-s coordinate. [Ans:- For process 1-2, S2 - S1 = 0.025 kJ/K For process 2-3, S3 - S2 = -0.035 kJ/K For process 3-1, S3 - S1 = 0.0099 kJ/K] AU Problem 3.11 Find the change in entropy of 1 kg of ice which is heated from -5°C to 0°C. It melts into water at 0°C. Cpice = 2.093 kJ/kgK. The pressure during heating is maintained at 1 atm constant. Latent heat of fusion of ice = 334.96 kJ/kg. Given data: m = 1 kg Tice - 5°C = -5 + 273 = 268 K To = 0°C = 0 + 273 = 273 K Cpice = 2.093 kJ/kgK L = 334.96 kJ/kg To find: ΔS Solution: Entropy change of system, ΔSsystem = ΔSice + ΔSfusion AU Problem 3.12 One kg of ice at -5°C is exposed to the atmosphere which is at 20°C. The ice melts and comes into thermal equilibrium with the atmosphere (i) Determine the entropy increase of the turbine. (ii) What is the minimum amount of work necessary to convert the water back to ice at -5°C? Assume C, for ice as 2.093 kJ/kg K and latent heat of fusion of ice as 333.3 kJ/kg. Given data: T1 = -5°C = 273 – 5 = 268 K Ta = 20°C = 273 + 20 = 293 K Cp = 2.093 kJ/kgK L = 333.3 kJ/kg To find: ΔSmin and Wmin Solution: Heat absorbed by air from atmosphere, δQ = Heat absorbed in solid phase + Latent heat + Heat absorbed in liquid phase If water is to be converted back to ice using a reversible refrigerator, heat to be removed from water and power input or work should be supplied. δQ = 427.505 kJ Now, ΔSsys = -1.556 kJ/K AU Problem 3.13 Ten grams of water at 20°C is converted into ice at -10°C at constant atmospheric pressure. Assuming the specific heat of liquid water to remain constant at 4.2 J/gK and that of ice to be half of this value and taking the latent heat of fusion of ice at 0°C as 335 J/g, calculate the entropy change of the system. Same as Problem 3.5 on Page 3.21. AU Problem 3.14 One kg of ice at -10°C is allowed to melt in atmosphere at 30°C. The ice melts and the water so formed rises in temperature to that of atmosphere. Determine the entropy change of ice, entropy change of surrounding and entropy change of Universe and write your comment based on principle of increase in entropy. The specific heat of ice is 2 kJ/kgK and its latent heat is 335 kJ/kg. Similar to AU Problem 3.12 on Page 3.41. [Ans:- ΔSice = 0.0746 kJ/K, ΔSatm.= -1.588 kJ/K, ΔSsystem = 1.74 kJ/K and ΔSUniv. = 0.152 kJ/K] AU Problem 3.15 50 kg of water is at 313 K and enough ice at -5°C is mixed with water in an adiabatic vessel such that at the end of the process all the ice melts and water at 0°C is obtained. Find the mass of ice required and entropy change of water and ice. Given Cp of water = 4.2 kJ/kgK, Cp of ice = 2.1 kJ/kgK and latent heat of ice = 335 kJ/kg. Given data: mw = 50 kg Tw = 313 K Tice = -5°C = -5 + 273 = 268 K Tf = 0°C = 0 + 273 = 273 K Cpw = 4.2 kJ/kgK Cp1 = 2.1 kJ/kgK Latent heat of ice = 335 kJ/kg Solution: Energy balance equation becomes AU Problem 3.16 2 kg of water at 90°C is mixed with 3 kg of water at 10°C in an isolated system. Calculate the change of entropy due to the mixing process. Similar to Problem 3.7 on Page 3.23. [Ans:- Change in entropy, ΔS = 0.038 kJ/K] AU Problem 3.17 A metal block with m = 5 kg, C = 0.4 kJ/kgK at 40°C is kept in a room at 20°C. It is cooled in the following two ways: (1) Using a Carnot engine (executing integral number of cycles) with the room itself as the cold reservoir; (2) Naturally. In each case, calculate the change in entropy of the block, air in the room and universe. Assume that the metal block has constant specific heat. Given data: m = 5 kg Cm = 0.4 kJ/kg K T1 = 40°C = 273 + 40 = 313 K T2 = 20°C = 273 + 20 = 293 K Solution: (i) Cooling naturally: Heat absorbed by air, δQ = Heat released by the metal block (ii) Cooling using a Carnot engine: If the metal block cools naturally, heat removed from metal block. δQ = 40 kJ AU Problem 3.18 A 30 kg iron block and a 40 kg copper block, both initially at 80°C, are dropped into a large lake at 15°C. Thermal equilibrium is established after a while as a result of heat transfer between blocks and lake water. Determine the total entropy change for this process. Given data: miron = 30 kg mcopper = 40 kg Tiron = Tcopper = 80°C = 273 + 80 = 353 K Tlake = 15°C = 273 + 15 = 288 K Solution: Heat absorbed by lake from both blocks, δQ = Heat released by iron block + Heat released by copper block AU Problem 3.19 One kilogram of water at 273 K is brought into contact with a heat reservoir at 373 K. (i) When the water has reached 373 K, find the change in entropy of the water, of the reservoir and universe. (ii) If the water had been heated from 273 K to 373 K by first bringing it in contact with a reservoir at 323 K and then with a reservoir at 373 K, what would have been the change in entropy of the universe. Given data: mw = 1 kg T1 = 273 K T2 = 373 K Tw = 273 K = T1 Cpw = 4.187 kJ/kgK Solution: Case (i): Entropy of universe, ΔSUniv = ΔSsystem or ΔSWater + ΔSReservior Entropy change of reservoir, Case (ii): Water is heated in two stages such as first from 273 K to 323 K by a reservoir at 323 K and then from 323 K to 373 K by another reservoir at 373 K. So, T1 = 273 K, T2 = 323K and T3 = 373 K Entropy of universe is calculated by AU Problem 3.20 Three identical bodies of A, B and C with constant heat capacity are at temperatures of 300 K, 300 K and 100 K. A heat engine is operated between A and B and a heat pump working as refrigerator is operated between B and C. The heat pump is operated by the output of heat engine. If no work or heat supplied from outside, find the highest temperature to which any one of the body can be raised by the operation of heat engine or refrigerator. Solution: A heat engine and a heat pump are operated between temperature limits 300 K, 300 K and 100 K. Let Tf be the final temperature of bodies A and B. Tf′ be the final temperature of body C and C be the final heat capacity of these three identical bodies. Missing 3.50 electrical energy, water power, wind power, tidal power, kinetic energy of jet etc. come under the category of high grade energy. (ii) Low grade energy: The energy which cannot completely be converted into high grade energy is called low grade energy. The partial conversion of low grade energy to high grade energy is possible. Based on the second law of thermodynamics, the possible conversion of low grade energy is known as available energy. At the same time, the unavoidable rejection of low grade energy to the sink or atmosphere is called unavailable energy. Generally, the thermal energy is considered as low grade energy. For example, heat or thermal energy, heat released during nuclear fission process and heat released during combustion of fossil fuels are considered as low grade energy. Based on the concept of various grades of energy, the following statements are arrived: 1. The first law of thermodynamics does not deal with the same grade of energy and its feasibility but it says that all the energy absorbed is converted into work output without losses. [⸫ Work is a high-grade energy and heat is a low grade energy. ⸫ η1 = 100% where Q = W] 2. The second law of thermodynamics says that all the energy absorbed as heat by an engine cannot be converted into work. Some part of the energy must be rejected to sink. Q1 = W + Q2 [ ⸫ W ➡ Useful work and Q2 ➡ Losses] Losses occur due to friction called irreversibility. It is already mentioned in entropy.







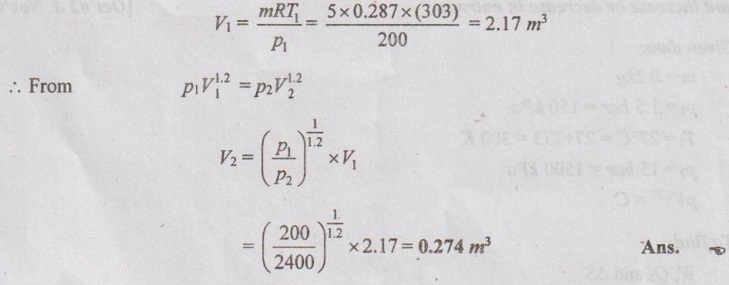



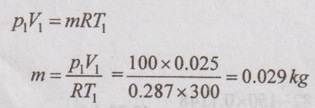




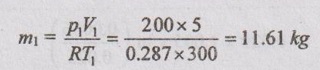



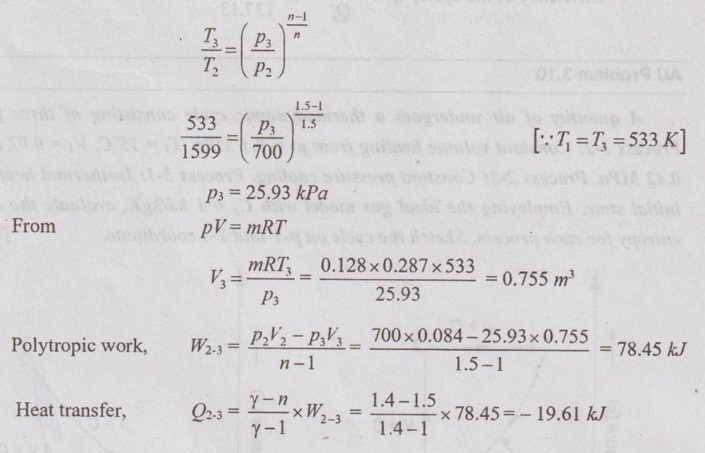








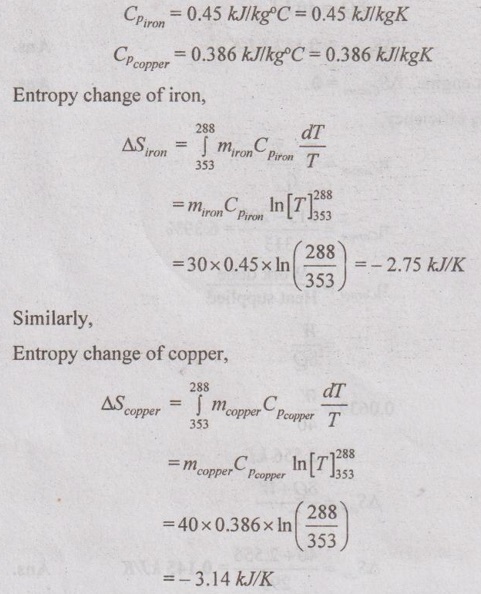






Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : Thermodynamics - Solved Anna University Problems on Entropy principles
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
