Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations
Solutions of one dimensional wave equation
Solved Example Problems | Partial Differential Equations
Equation of a vibrating string :- One dimensional wave equation: Consider an elastic string tightly stretched between two points O and A. Let O be the origin and OA as x-axis.
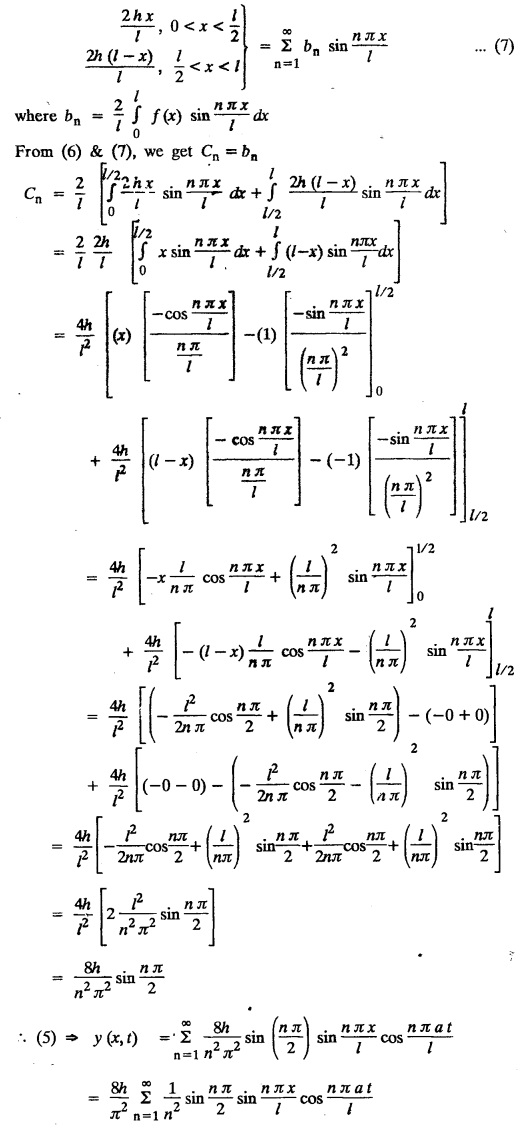
SOLUTIONS OF ONE DIMENSIONAL WAVE EQUATION Equation of a vibrating string :- One dimensional wave equation: Consider an elastic string tightly stretched between two points O and A. Let O be the origin and OA as x-axis. On giving a small displacement to the string, perpendicular to its length (parallel to the y-axis). Let y be the displacement at the point P (x, y) at any time. The wave equation is Example 3.3.1: Obtain the solution of one dimensional wave equation: Solution: One dimensional wave equation is Solve this by using method of separation of variables. where X is a function of x alone and T is a function of t alone. ⸫ differentiate (2) partially, we get The nature of the solutions of (6) & (7) depends on the value of k. Case (i) Let k be positive say k = p2 Case (ii) Let k be negative say k = -p2 Case (iii) Let k = 0 Thus the various possible solutions of the wave equations are Out of the three mathematically possible solutions derived, we have to choose the solution which is consistent with the physical nature of the problem and the given boundary conditions. In the case of vibration of an elastic string, y (x, t) representing the displacement of the string at any point x, y must be periodic in t. Hence solution (9), which consists of periodic functions in t is the suitable solution of the problems on vibration of strings. The arbitrary constants in the suitable solution are found out by using the boundary conditions of the problem. In problems, we directly assume that (9) is the suitable solution of vibration of string problems. The suitable solution (9) which is periodic in ' is incidentally periodic in 'x' also. Example 3.3.2: Derive D' Alembert's solution of the wave equation: Solution: Consider the one dimensional wave equation From (3) & (4), we get This solution is called D' Alemberts solution of the one dimensional wave equation. Example 3.3.3: State the assumptions made in the derivation of one dimensional wave equation. Solution: The wave equation is This gives y (x, t), the transverse vibration of a string stretched to a constant tension T. In deriving this equation, we make the following assumptions. 1. The motion takes place entirely in one plane i.e., xy plane. 2. We consider only transverse vibrations, the horizontal displacement of the particles of the string is negligible. 3. The tension T is constant at all times and at all points of the deflected string. 4. T is considered to be so large compared with the weight of the string and hence the force of gravity is negligible. 5. The effect of friction is negligible. 6. The string is perfectly flexible, i.e., it can transmit tension but not bending or shearing forces. 7. The slope of the deflection curve at all points and at all instants is so small that sin α can be replaced by α, where a is the inclination of the tangent to the deflection curve. Example 3.3.4: Derive one dimensional wave equation : Solution : Consider a tightly stretched elastic string of length l with its end points fixed. Let the string be released from rest and allowed to vibrate. The problem is to determine the deflection y (x, t) at any point x and at any time t > 0. For deriving the p.d.e. we make the following assumption. See Example 3.3.3. To obtain the differential equation Take one end of the string as origin O and take X-axis along the string. We assume that the motion takes place entirely in the XY plane. Consider the forces acting on a small portion PQ of the string where P is (x, y) and Q is (x + Δx, y + Δy) By assumption, the string does not offer resistance to bending and shearing hence the tension at each point of the string is tangential to the curve of the string. Let T1 and T2 be the tensions at the points P and Q. Let ψ and ψ + Δψ be the angles made by the tangents at P and Q respectively with the X axis. Let m be the mass per unit length of the string Since, there is no motion in the horizontal portion of the string the tension must be constant. ⸫ T1 cos ψ = T2 cos (ψ + Δψ) which is a constant. Since ψ is small, cos ψ and cos (ψ + Δψ) are approximately equal to 1. Thus, T1 = T2 = T, a constant. The vertical component of the force acting on the element PQ is T sin (ψ + Δψ) – T sin ψ = T (ψ + Δψ) − T ψ [⸪ sin ψ = ψ. where ψ is small] = TΔ ψ The acceleration of the element in the y direction is Hence, by Newton's second law of motion, This partial differential equation is known as the one dimensional wave equation. It is a homogeneous of second order. Example 3.3.5a: The p.d.e. of a vibrating string is Solution: Example 3.3.5b: Explain why a2 (instead of a) is used in the p.d.e. of the vibrating string Solution: Problem on vibrating string with zero initial velocity. Type 1. Vibrating string with zero initial velocity : The boundary and initial conditions of the deflection y (x, t) are Apply condition (iv), we get Substitute, Cn in (2) we get the general solution. Example 3.3.6 : A string is stretched and fastened to two points x = 0 and x = l apart. Motion is started by displacing the string into the form y = k (lx − x2) from which it is released at time t = 0. Find the displacement of any point on the string at a distance of x from one end at time t. Solution: The wave equation is Now, the suitable solution which satisfies our boundary conditions is given by Applying condition (i) in equation (1), we get Substitute, c1 = 0 in equation (1), we get Applying condition (ii) in equation (2), we get Before applying condition (iii), diff. (3) p.w.r.to 't’, we get Now applying condition (iii), we get The most general solution is Applying the condition (iv) in equation (5), we get To find Cn: expand k (lx − x2) in a half-range Fourier Sine Series in the interval (0, l) Substitute the value of Cn in equation (5), we get Example 3.3.7: Find the displacement of a string of length 'l' vibrating between fixed end points with initial velocity zero and initial displacement is given by Solution: The wave equation is From the given problem we get the following boundary and initial conditions. Now, apply condition (iv) in (5), we get To find Cn : Expand the given function in a half range Fourier sine series in the interval (0, l) Substitute Cn value in equation (5), we get Example 3.3.8: A string of length 2l is fastened at both ends. The mid point of the string is taken to a height b and then released from rest in that position. Show that the displacement is Solution: The wave equation is From the given problem, we get the following boundary and initial conditions. Equation of BA is Now, the suitable solution which satisfies our boundary conditions is given by Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Before applying condition (iii), diff (3) p.w.r.to t, we get Now, applying condition (iii) we get Substitute, c4 = 0 in equation (3), we get The most general solution is Applying condition (iv) in equation (5), we get To find Cn expand the given value in a half-range Fourier sine series in the interval (0, L) Here, L = 2l Substitute the value of Cn in equation (5), we get Example 3.3.9 : A tightly stretched string of length l has its ends fastened at x = 0 and x = l. The mid point of the string is then taken to a height h and then released from rest in that position. Obtain an expression for the displacement of the string at any subsequent time. Solution: The equation to be solved is From the given problem, we get the following boundary and initial conditions, Equation of DB is Applying condition (iv) in (5), we get To find Cn : Expand the value in a half-range sine series in the interval (0, l). Example 3.3.10 : The points of trisection of a string of length l with fixed ends aside through a distance h on opposite sides of the position of equilibrium and the string is released from rest. Find an expression for the displacement of the string at any subsequent time. Also show that the mid point of the string always remains at rest. Solution: Taking the end points as origin O and A on the x axis, the initial position of the string is given in the figure. Equation of EA is given by The displacement function y (x, t) of the string is the solution of wave equation. From the given problem, we get the following boundary and initial conditions, Applying the boundary condition (iv) in (5), we get To find Cn expand f(x) in a half range Fourier sine series in the intervel (0, l) The displacement at the mid point is got by substituting for all values of t. ⸫ The mid point of string is at rest. Example 3.3.11: If a string of length l is released from rest in the position Solution : The wave equation is From the given problem, we get the following boundary and initial conditions. Now, the suitable solution which satisfies our boundary conditions is given by Applying condition (iv) in equation (5), we get To find Cn: Expand Substitute the value of Cn in (5), we get Example 3.3.12: A tightly stretched string with fixed end points x = 0 and x = l__initially displaced in a sinusoidal arc of length y0 and then released from rest. Find the displacement y at any distance x from one end at time t. Solution: The wave equation is From the given problem, we get the following boundary and initial conditions, Now, the suitable solution which satisfies our boundary conditions is given by Applying the boundary condition (iv) in (5), we get To find Cn : Expand (6), we get Example 3.3.13 : An elastic, string is stretched between two points at a distance л apart. In its equilibrium position the string is in the shape of the curve f(x) = k (sin x sin3 x). Obtain y(x, t) the vertical displacement if y satisfies the equation Solution: The wave equation is The boundary & initial conditions are, Applying condition (iv) in (5), we get Equating like coefficients on both sides of (6), we get Substituting these values in (5), we get Example 3.3.14: A string of length l has its ends x = 0, x = l fixed. The point where x = l/3 is drawn aside a small distance h, the displacement y(x, t) satisfies Solution: The wave equation is From the given problem, we get the following boundary and initial conditions Applying the boundary condition (iv) in equation (5), we get To find Cn expand f(x) in a half-range Fourier sine series in the interval (0, l) 1. A uniform elastic string of length 60 cm is subjected to a constant tension of 2 kg. If the ends are fixed and the initial displacement is y (x, 0) = 60x - x2 for 0 < x < 60 while the initial velocity is- zero, find the displacement function y (x, t). 2. A tightly stretched string with fixed end points x = 0 and x = l is initially in a position given by If it is released from rest from this position find the displacement y at any distance x from one end at any time t. 3. A taut string of length 2l is fastened at both ends. The mid point of the string is taken to a height h and then released from rest in that position. Find the displacement of the string. 4. The points of trisection of a tightly stretched string of length 30 cm with fixed ends pulled aside through a distance of 1 cm on opposite sides of the position of equilibrium and the string is released from rest. Find an expression for the displacement of the string at any subsequent time, also show that the mid points of the string remains always at rest. 5. A string of length l is fastened at both ends. One end is taken as the origin and at a distance b from this end, the string is displaced a distance d transversely and is released from rest when it is in this position. Find the equation of the sub-sequent motion. 6. A tightly stretched flexible string has its ends fixed at x = 0 and x = l. At time t = 0 the string is given a shape defined by f(x) = μx (l-x) where u is a constant and then released. Find the displacement of the string at any time 't'. Problems on vibrating string with non-zero initial velocity. Type 2. Vibrating string with non-zero initial velocity : The boundary and initial conditions of the deflection y (x, t) are The suitable solution is The most general solution is Apply condition (iv), we get Substitute in (2) we get the general solution. Example 3.3.15: A tightly stretched string with fixed end points x=0 and x = l is initially at rest in its equilibrium position. If it is set vibrating string giving each point a velocity λ x (l − x) show that the displacement is Solution: The wave equation is From the given problem we get the following boundary and initial conditions, Now, the suitable solution which satisfies our boundary conditions is gien by Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Applying condition (iii) in equation (3), we get The most general solution is Before applying condition (iv), diff. (5) p.w.r.to ‘t’ we get Now, we apply condition (iv), we get To find Вn : Expand λ x (l − x) in a half range Fourier sine series in the interval (0, l) Substitute the value of Cn in equation (5) we get Example 3.3.16 : If a string of length a is initially at rest in its equilibrium position and each of its points is given a velocity kx (a − x), determine the displacement function. Solution: In Example 3.3.15 Put l = a and λ = k Example 3.3.17 : A tightly stretched string with fixed end points x = 0 and x = L, is initially in its equilibrium position. If it is set vibrating giving each point a velocity 3x (L − x), find the displacement. Solution: In Example 3.3.15 Here, Put l = L and λ = 3 Example 3.3.18: A tightly stretched string with fixed end points x = 0, and x = L is initially in a position given by y = Lx - x2 it is released from rest from this position, find the displacement y(x, t) Solution: In Example 3.3.15 Here, Put l = L and λ = 1 Example 3.3.19: If a string of length l is initially at rest in its equilibrium position and each of its points is given the velocity Solution: The wave equation is From the problem we get the following boundary and initial conditions Now, the suitable solution which satisfies our boundary condition is given by From equation (5), we get Example 3.3.20 : A string of length l is initially at rest in its equilibrium position and motion is started by giving each of its points a velocity given by Solution: The wave equation is From the given problem we get the following boundary and initial conditions, Now, the suitable solution which satisfies our boundary conditions is given by Before applying condition (iv), diff (5) p.w.r. to 't', we get Now, we apply condition (iv), we get To find Bn: Expand f(x) in a half range Fourier sine series in the interval (0, l) Example 3.3.21: If the string of length l is initially at rest in equilibrium given the position and each of its points is given the velocity Solution: The wave equation is From the given problem, we get the following boundary and initial conditions, Now, the suitable solution which satisfies our boundary conditions is given by Before applying condition (iv), differentiate (5) p.w.r. to 't’, we get Now apply condition (iv), we get Equating the like terms, we get Substitute the values in equation (5), we get Example 3.3.22 : A string is stretched between two fixed points at a distance 2l apart and the points of the string are given initial velocities v where x being the distance from one end point. Find the displacement of the string at any subsequent time. Solution: The wave equation is From the given problem, we get the following boundary and initial conditions, The most general solution is Before applying condition (iv), differentiate (5) p.w.r.to 't', we get Now we apply condition (iv), we get To find Bn expand f (x) in a Half range Fourier sine series in the interval (0, 2l) 1. A taut string of length 20 cm fastened at both ends is displaced from its position of equilibrium by imparting to each of its points an initial velocity given by x being the distance from one end. Determine the displacement at any subsequent time. 2. A string is stretched between two fixed points at a distance of 60 cm and the points of the string are given initial velocities v, where x being the distance from an end point. Find the displacement of the string at any time. 3. Solve the boundary value problem 4. Solve ANSWERS Type 3. Vibrating string initial velocity and initial displacement given: The initial and boundary conditions are Apply condition (iii), we get Apply condition (iii), we get Substitute, Cn, Dn values in (2), we get the general solution. PROBLEM ON VIBRATING STRING WITH INITIAL VELOCITY AND INITIAL DISPLACEMENT GIVEN Example 3.3.23 : Solve the problem of the vibrating string for the following boundary conditions: (i) y (0, t) = 0, (ii) y (l, t) = 0 Solution: The wave equation is From the given problem, we get the following boundary and initial conditions Now, the suitable solution which satisfies our boundary conditions is given by Applying condition (i) in equation (1), we get Applying condition (ii) in (2), we get The most general solution is Before applying condition (iii) diff (4) p.w.r.to 't', we get Now, applying condition (iii), we get We now express x (x − l) as a half range Fourier sine series in (0, l) Now, we apply condition (iv) in (5), we get We express f(x) as a half range Fourier sine series in (0, l) Sub in equation (5) we get EXERCISE 3.3(c) 1. A string is stretched between two fixed points at a distance of л cm and the points of the string are given initial velocities v, where 2. Find the displacement of a tightly stretched string of length 7 cm vibrating between fixed end points, if initial displacement is







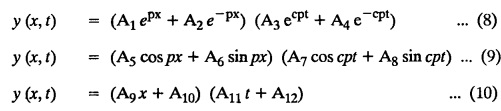






 what is a2?
what is a2?



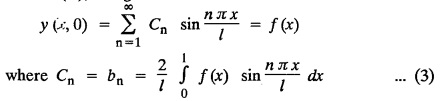

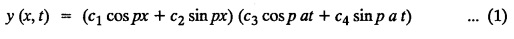



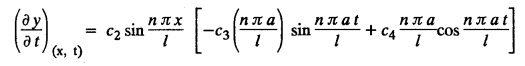









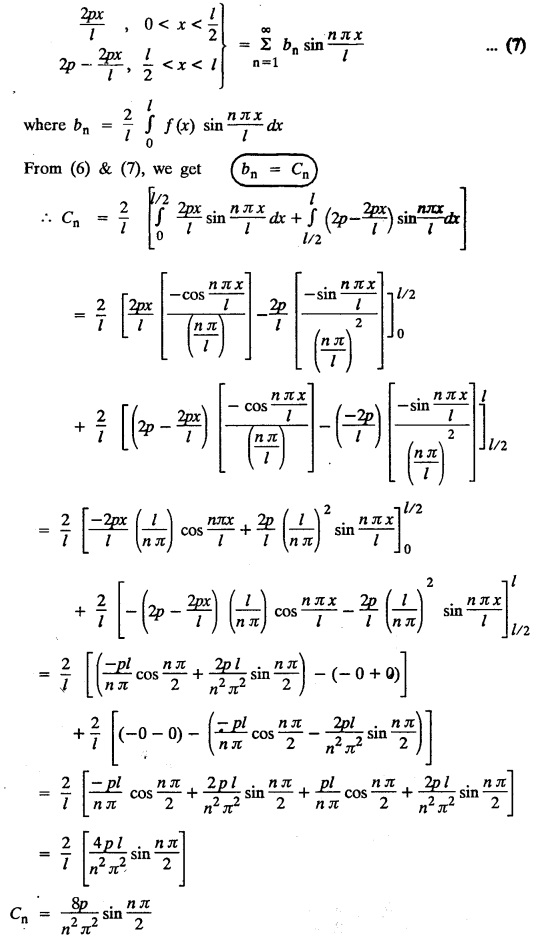
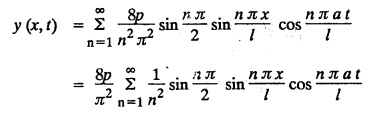



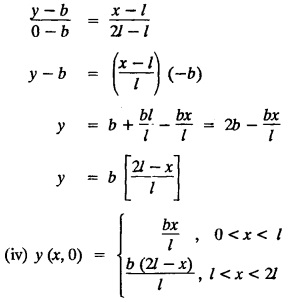
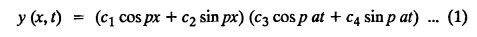



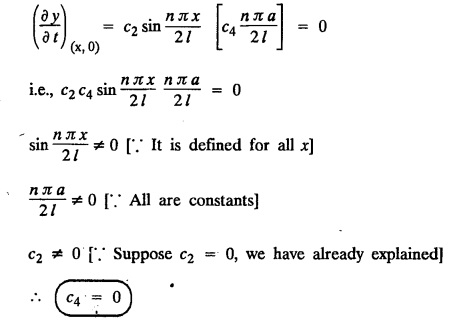




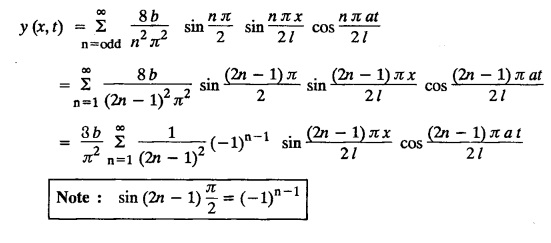






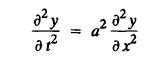

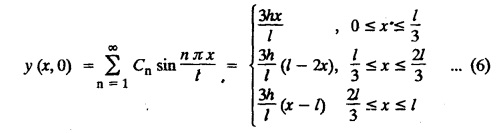


 Show that the motion is described by the equation.
Show that the motion is described by the equation. 




 in a half range Fourier sine series in the interval (0, l)
in a half range Fourier sine series in the interval (0, l)

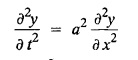


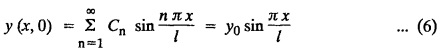




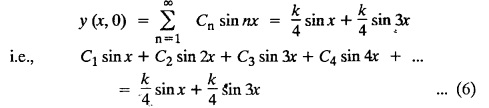

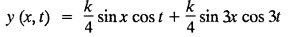
 Find y(x, t) at any time t.
Find y(x, t) at any time t.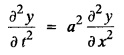


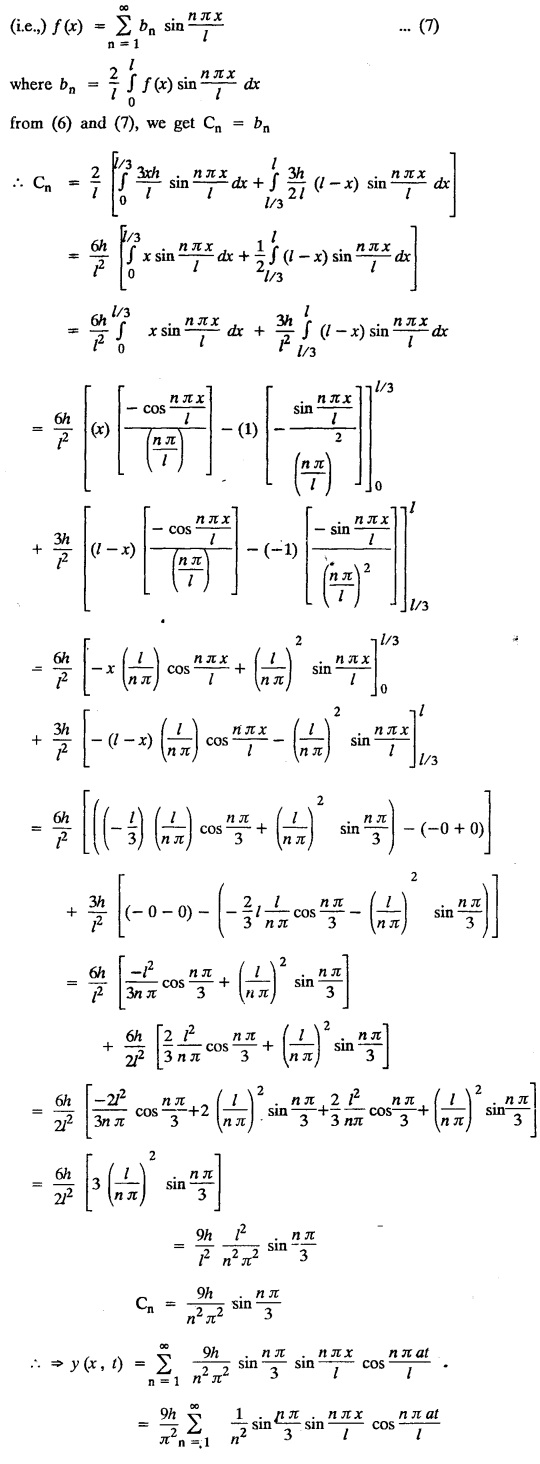
EXERCISE 3.3(a)

ANSWERS
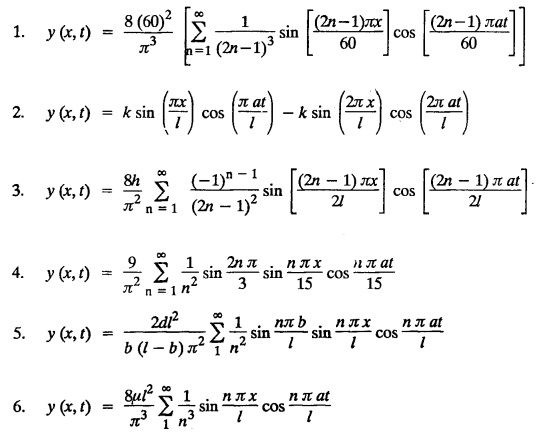











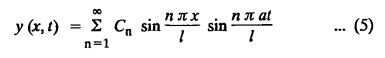

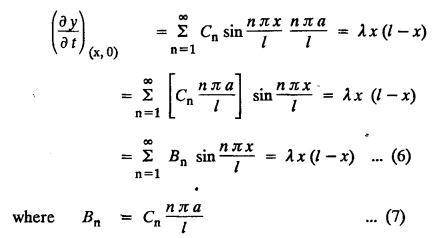


 determine the displacement of a point distant x from one end at time ‘t'.
determine the displacement of a point distant x from one end at time ‘t'.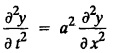



 Find the displacement function y (x, t).
Find the displacement function y (x, t). 





 determine the displacement function y(x, t)
determine the displacement function y(x, t)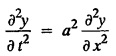







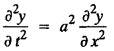
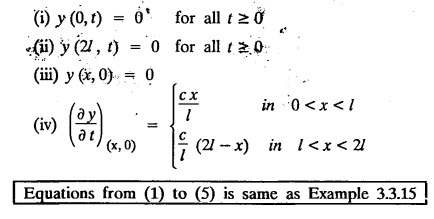


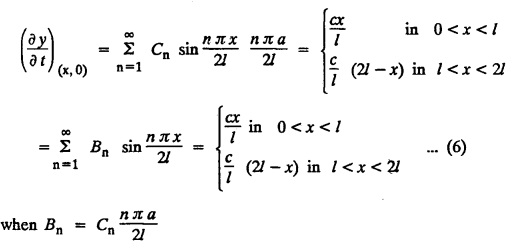

EXERCISE 3.3(b)





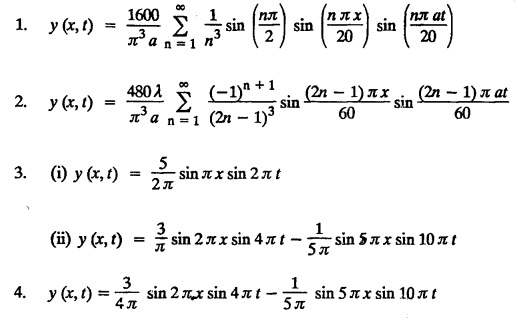

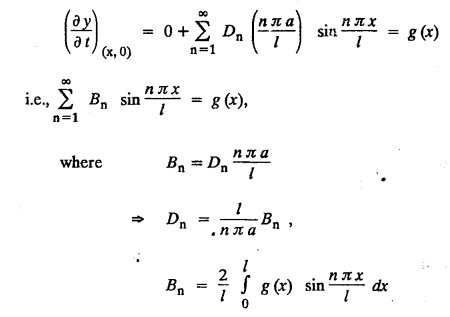


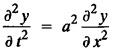









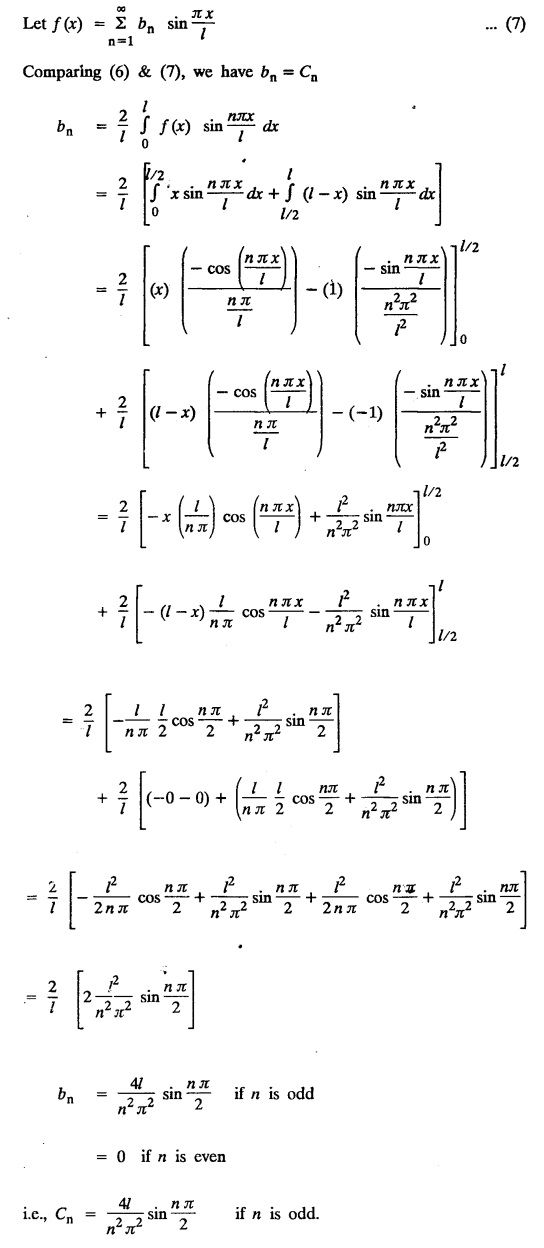



Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations : Tag: : Solved Example Problems | Partial Differential Equations - Solutions of one dimensional wave equation
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
