Transforms and Partial Differential Equations: Unit I: Partial Differential Equations
Singular integrals grals - solution of standard types of first order partial differential equations
Solved Example Problems
(a) Problems based on General solution of p.d.e in ordinary cases:
SINGULAR INTEGRALS GRALS - SOLUTION OF STANDARD TYPES OF FIRST ORDER PARTIAL DIFFERENTIAL EQUATIONS III. (a) Problems based on General solution of p.d.e in ordinary cases: Example 1.3(a)(1): Solve Solution: Example 1.3(a)(2): Find the general solution of Solution : Example 1.3(a)(3): Solve Solution: Example 1.3(a)(4): Solve Solution: Here both F(y) and ϕ (x) are arbitrary. Example 1.3(a)(5): Solve : Solution : Example 1.3(a)(6): Solve Solution : z is a function of x alone Since z is a function of x and y. Therefore A & B will be the functions of y alone. Hence I. Solve the following partial differential equation. ANSWERS 1.3(2) Methods to solve the first order partial differential equation. The general form of a first order partial differential equation is f(x, y, z, p, q) = 0, where p § Mention three types of solution of a p.d.e. (or) Define P.I, general and complete integrals of a p.d.e. 1. Complete integral (or) Complete solution A solution which contains as many arbitrary constants as there are independent variables is called a complete integral (or) complete solution. (number of a.c. number of I.V) 2. Particular integral (or) Particular solution A solution obtained by giving particular values to the arbitrary constants in a complete integral is called a particular integral (or) particular solution. 3. General integral (or) General solution A solution of a p.d.e. which contains the maximum possible number of arbitrary functions is called a general integral (or) general solution. Example (i): z = ax + by + ab Example (ii) : z = 2x + 3y + 6 is a particular integral. Since, a = 2, b = 3 are the particular values of the complete integral z = ax + by + ab Example (iii) : z = ƒ (x2 − y2) ... (1) is the solution of p.d.e yp + xq = 0 ... (2) Here, yp + xq = 0 is a p.d.e of order 1. So, the maximum possible number of a.f. = 1 ⸫ z = f(x2 - y2) is a general solution of (2). § Show how to find the general integral of the p.d.e. f (x, y, z, p, q) = 0. Solution : Let the p.d.e. be f (x, y, z, p, q) = 0 …(1) Let the complete integral of (1) be ϕ (x, y, z, a, b) = 0 ….(2) where a & b are arbitrary constants. Suppose, in (2) one of the constants is a function of the other say b = f(a). Then (2) becomes Differentiating (3) p.w.r. to a we get The elimination of 'a' between (3) & (4) if it exists, is called the general integral of (1). § Define singular integral. Solution : Let f (x, y, z, p, q) = 0 ….(1) Let the complete integral be ϕ (x, y, z, a, b) …(2) Differentiating (2) p.w.r. to a and b in turn we get, The elimination of a & b from the three equations (2), (3) & (4) if it exists, is called the singular integral. Type 1 f(p, q) = 0 Suppose that z = ax + by + c then p = a, q = b we get, f (a, b) = 0 solving for b, we get b = ϕ (a) z = ax + ϕ (a) y + c …(1) which is the required complete integral. Differentiating (1) p. w.r.to c, we get 0 = 1 which is absurd that there is no singular integral. Put c = f (a) in (1) we get z = ax + ϕ (a) y + f (a) …(2) Differentiating (2) p. w.r.to a we get 0 = x + ϕ' (a) y + f'(a) ….(3) eliminating 'a' between (2) and (3), we get the general solution. Problems based on Type 1 f (p, q) = 0 Example 1.3(b)(1) : [Type 1] Solve: √p + √q = 1 Solution: Given : √p + √q = 1 …(1) This equation is of the form f (p, q) = 0 …(2) Hence, the trial solution is z = ax + by + c …(3) To get the complete integral (solution) Since, number of a.c. = number of I.V. To find the singular integral : Differentiating (4) p.w.r.to c we get, 0 = 1 [absurd] Hence, there is no singular integral. To get the general integral (solution) Put, c = f (a) in (4), we get Differentiating partially w.r.to ‘a', we get Eliminating 'a' between (5) and (6), we get the general solution of the given p.d.e. Example 1.3b(2): [Type 1] Solve p+q= pq Solution: Given: p + q = pq ….(1) This equation is of the form ƒ (p,q) = 0 …. (2) Hence, the trial solution is z = ax + by + c …. (3) To get the complete integral (solution) Since, number of a.c. = number of I.V To find the singular integral : Differentiating (4) p.w.r.to c we get, 0 = 1 [absurd] Hence, there is no singular integral. To get the general integral (solution) Put c = f(a) in (4), we get differentiating partially w.r.to ‘a', we get Eliminating 'a' between (5) & (6), we get the general solution of the given p.d.e. Example 1.3b(3): [Type 1] Solve: pq = k Solution: Given: pq = k …(1) This equation is of the form ƒ (p, q) = 0 …(2) Hence, the trial solution is z = ax + by + c ….(3) To get the complete integral : Since, number of a.c.= number of I.V. To find the singular integral Differentiating (4) p.w.r.to c we get, 0 = 1 [absurd] There is no singular integral. To get the general integral (solution) Put c = f (a) in (4), we get differentiating p.w.r to 'a', we get Eliminating 'a' between (5) & (6), we get the general solution of the given p.d.e. Example 1.3b(4) [Type 1] Solve: p2 + q2 = npq Solution: Given: p2 + q2 = npq ... (1) This equation is of the form ƒ (p, q) = 0 ….(2) Hence, the trial solution is z = ax + by + c ….(3) To get the complete integral (solution) : Since, number of a.c. = number of I.V To find the singular integral : Differentiating (4) p.w.r.to c we get, 0 = 1 [absurd] There is no singular integral. To get the general integral (solution) Put c = ϕ(a) in (4), we get Eliminating 'a' between (5) & (6), we get the general solution of the given p.d.e. Note: Solve p2 + q2 - 4pq = 0 In the above problem put n = 4 we get the solution. Example 1.3b(5) : [Type 1] Find the complete integral of p − q = 0 Solution: Given p − q = 0 ... (1) This equation is of the form ƒ (p, q) = 0 ...` (2) Hence, the trial solution is z = ax + by + c …(3) To get the complete integral (solution) ⸫ (1) ⇒ a – b = 0 b = a. Hence, the complete integral is z = ax + ay + c. Hence, number of a.c. = number of I.V. [We can get general solution easily by using Lagrange's idea] Find the complete integral of the following equations. Problems based on Type 2. TYPE 2. Clairaut's form z = = px + qy + f (p, q) Example 1.3b(6): Solve z = px + qy + pq and classify the following integrals (i) z = ax + by + ab; (ii) z = 2x + 3y+6 (iii) z + xy = 0 Solution: Given: z = px + qy + pq This equation is of the form z = px + qy + f (p,q) Therefore, the complete integral is z = ax + by + f (a, b) i.e., z = ax + by + ab …(1) To find the singular integral differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get To get the general integral, put b = ϕ (a) in (1), we get z = ax + ϕ (a) y + a ϕ (a) …(5) differentiating (5) p.w.r.to a, we get 0 = x + ϕ' (a) y + a ϕ' (a) + ϕ(a) .... (6) Eliminating ‘a' between (5) & (6), we get the general solution. Classification of integrals (i) z = ax + by + ab is a complete integral. (ii) z = 2x + 3y + 6 is a particular integral. Since, Here a = 2, b = 3 (iii) z + xy = 0 is a singular integral. Example 1.36(7): Solve z = px + qy + p2 - q2. Solution: Given: z = px + gy + p2 - q2 This equation is of the form z = px + qy + f (p, q) [Clairaut's type] Therefore, the complete integral is z = ax + by + a2 − b2 ….(1) Since the number of a.c. = number of I.V To find the singular integral. differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get 4z = -x2 + y2 is the singular solution. To get the general integral. put b = ϕ (a) in (1), we get z = ax + ϕ (a) y + a2 - [ϕ (a)]2 …(4) differentiating (4) p.w.r. to 'a', we get 0 = x + ϕ' (a) y + 2a - 2 ϕ(a) ϕ' (a) …. (5) Eliminating 'a' between (4) & (5), we get the general solution. Example 1.3b(8) : Find the complete integral of (p − q) (z - px - qy) = 1. Solution: This equation is of the form z = px + qy + f (p, q) [Clairaut's equation] Therefore, the complete integral is Since, the number of a.c. = number of I.V Example 1.3b(9): Find the singular integral of z = px + qy + p2 Solution: Given: z = px + y + p2 This equation is of the form z = px + qy + f (p, q) [Clairaut's type] Therefore, the complete integral is z = ax + by + a2 ….(1) Since the number of a.c. = number of I.V To get the singular integral. differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get 4z + x2 = 0 is the singular integral. Example 1.3b(10) : Solve z = px + qy + p2 q2. Solution: Given: z = px + qy + p2 q2 This is Clairaut's form, The complete solution is z = ax + by + a2 b2 … (1) Since, the number of a.c. = number of I.V To get the singular integral, differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get 16z3 + 27x2y2 = 0 is the singular solution. To get the general integral. put, b = ϕ(a) in (1) differentiating (6) w.r.to a, we get eliminate 'a' between (6) & (7), we get the general solution. Example 1.3b(11) : Solve z = px + qy + Solution: Given: z = px + qy + This is of the form z = px + qy + f (p, q) [Clairaut's form] Hence, the complete integral is z = ax + by + where a and b are arbitrary constants. Since the number of a.c. = number of I.V To get the singular integral : differentiating (1) p.w.r. to ‘a', we get differentiating (1) p.w.r. to 'b', we get x2 + y2 + 22 = 1 is the singular solution. To get the general integral, put b = ϕ(a) in (1), we get differentiating (5) p.w.r. to 'a', we get eliminate 'a' between (5) & (6), we get the general solution. Example 1.3.b(12): Solve Solution: This is of the form z = px + qy + f (p, q) [Clairaut's form] Hence, the complete integral is where a and b are arbitrary constants. To get the singular integral : differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get To get the general integral, put, b = ϕ (a) in (1), we get differentiating (4) p.w.r. to ‘a', we get eliminate ‘a' between (4) & (5), we get the general solution. Example 1.3b(13) : Obtain the complete solution of the equation z = px + qy − 2 √pq. Solution: Given: z = px + qy -2 √pq This is of the form z = px + qy + f (p, q) [Clairaut's form] Hence, the complete solution is z = ax + by - 2 √ab where a and b are arbitrary constants. Since, the number of a.c. = number of I.V Example 1.3b(14) : Solve z = px + qy + (pq)3/2. Solution: Given : z = px + qy + (pq)3/2 This is of the form z = px + qy + f (p, a) [Clairaut's form] Hence, the complete integral is z = ax + by + (ab)3/2 ….(1) Since, the number of a.c. = number of I.V To find the singular integral, differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get Example 1.3b(15) : Find the singular integral of z = px + qy + p2 + q2 Solution : z = px + qy + p2 + q2 …. (1) This equation is of the form z = px + qy + f (p, q) [Clairaut's type] Therefore, the complete integral is z = ax + by + a2 + b2 Since, the number of a.c. = number of I.V To get the singular integral differentiating (1) p.w.r.to 'a' & 'b' we get Example 1.3b(16) : Find the complete integral of the partial differential equation (1 - x) p + (2 − y) q = 3 -z Solution: Given (1 − x) p + (2 − y) q = 3 - z p - px + 2q – qy = 3 - z z = px + qy – p - 2q+3 This equation is of the form z = px + qy +ƒ (p, q) [Clairaut's type] Hence, the complete integral is z = ax + by – a - 2b + 3 Since, the number of a.c. = number of I.V Example 1.3b(17) Find the singular integral of z = px + qy + p2 + pq + q2 Solution: Given: z = px + qy + p2 + pq + q2 i.e., z = px + qy + f (p, q) This equation is of the Clairaut's form. Hence, the complete solution is z = ax + by + a2 + ab + b2 ...(1) Since, the number of a.c. = number of I.V To find the singular integral. differentiating (1) p.w.r. to 'a', we get differentiating (1) p.w.r. to 'b', we get 3z = -x2 - y2 + xy 3z + x2 + y2 – xy = 0 is the singular integral. Example 1.3b(18): Solve the equation (pq-p-q) (z px qy) = pq Solution: Rewriting the given equation as This is of the form z = px + qy + f (p, q) [Clairaut's form] Hence, the complete solution is Since, the number of a.c.= number of I.V To find the singular solution of (1). differentiating (1) p.w.r. to ‘a', we get differentiating (1) p.w.r. to 'b', we get Find the complete solution and singular integral of the following: 1. z = px + qy = log pq [Ans. C.S is z = ax + by + log ab S.I is z = -2 - log (xy)] 2. z = px + qy + 3 (pq)1/3 [Ans. C.S is z = ax + by + 3 (ab)1/3 S.I is xyz = 1 ] 3. z = px + qy + 2 √pq [Ans. C.S is z = ax + by + 2 √ab S.I is xy =1] 6. Verify that z = ax + by + a/b is a complete solution of the equation z = px + qy + p/q. Show that the singular solution is zx + y = 0 i.e., equations not containing x and y. Let z be a function of u where u = x + ay Substitute the values of p and q in the given equation ƒ (z, p, q) = 0, it becomes f(z, a) = u + b = x + ay + b This is the complete integral, singular and general integral are found out as usual. Rule: Assume u = x + ay; replace p and q by Type 3 (b) Equation of the type f(x, p, q) = 0 ….(1) i.e., equations not containing y and z. Let z is a function of x and y Assume that, q = a Then the equation becomes ƒ (x,p,a) = 0 Solving for p, we obtain p = ϕ (x, a) dz = ϕ (x, a) dx + a dy Integrating we get, equation (2) is the complete integral of (1) since it contains two arbitrary constants, a & b Type 3 (c) Equation of the type f(y, p, q) = 0 ….(1) i.e., equations not containing x and z. Assume, p = a and proceed as Type 3 (b) The complete integral will be of the form z = ax + f (y, a) + b Problems based on types 3(a) f(z, p, q) = 0 Example 1.3b(18): Solve p (1 + q) = qz. Solution: Given : p (1 + q) = qz ….(1) This equation is of the form f (z, p, q) = 0 [Type 3(a)] Let u = x + ay Integrating on both sides, we get u = log (az - 1) - b ⇒ u+b = log (az - 1) Hence, the complete solution is x + ay + b = log [(az - 1)] Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(19): Solve p (1 + q2) = q (z − a) Solution: Given: p (1 + q2) = q (z − a) …. (1) This equation is of the form f (z, p, q) = 0 [Type 3(a)] Let u = x + by substituting these values of p & q in (1), we have Hence, the complete solution is 4 (bz - ab - 1) = (x + by + c)2 [Here, a is a given constant, b and c are arbitrary constants] Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(20): Solve z2 = 1 + p2 + q2. Solution: Given: z2 = 1 + p2 + q2 ….(1) The given problem is, of the type ƒ (z, p, q) = 0 [Type 3(a)] Let u = x + ay substitute in (1), we get Integrating on both sides, we get Hence, the complete solution is Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(21) : Solve 9 (p2z + q2) = 4. Solution: Given: 9 (p2z + q2) = 4 …(1) This equation is of the form ƒ (z, p, q) = 0 [Type 3(a)] Let u = x + ay substituting in (1), we get Integrating on both sides, we get Hence, the complete solution is ⇒ (z + a2)3 = (x + ay + b)2 Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(22): Solve z = p2 + q2. Solution : Given : z = p2 + q2 …. (1) This equation is of the form ƒ (z, p, q) = 0 [Type 3(a)] Let u = x + ay substituting in (1), we get Integrating on both sides, we get Hence, the complete solution is Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(23): Solve Ap+ Bq + Cz = 0. Solution: Given Ap + Bq + Cz = 0 …(1) This is of the form ƒ (z, p, q) = 1 [Type 3(a)] Let u = x + ay substituting in (1), we get Integrating on both sides, we get is the complete solution. [Here, A, B, C are given constants] Since, the number of a.c. = number of I.V General integral can be found out in a usual way. Example 1.3b(24): Solve p(1 − q2) = q(1 − z). Solution: Given: p (1 − q2) = q (1 − z) ... (1) This equation is of the form f (z, p, q) = 0 Let u = x + ay Squaring in both sides, we get 4 (1 − a + az) = (u + b)2 4 (1 − a + az) = (x + ay + b)2 which gives the complete integral of the given equation. Since, the number of a.c. = number of I.V General integral can be found out in a usual way. EXERCISE 1.3(b) Type 3 (Case i) f(z, p, q) = 0 Find the complete integrals of the following : Problems based on Type 3(b) f(x, p, q) = 0 Example 1.3b(25): Solve p = 2qx. Solution: Given: p = 2qx, this equation is of the form f (x, p, q) = 0. Let q = a [Type 3(b)] Then p = 2ax But, dz = pdx + qdy dz = 2ax. dx + ady Integrating on both sides, we get z = ax2 + ay + b ... (1) equation (1) is the complete integral of the given equation. Since, the number of a.c. = number of I.V Differentiating partially w.r.to b, we get 1 = 0. Hence, there is no singular integral. General integral can be found out in the usual way. [We can solve this easily by using Lagrange's idea] Example 1.3b(26) : Solve q = px + p2. Solution: Given : q = px + p2 ….(1) This equation is of the form f (x, p, q) = 0 [Type 3(b)] Assume q = a (constant) Then p2 + px – a = 0 We know that, dz = pdx + qdy Integrating on both sides, we get is the complete solution. Since, the number of a.c. = number of I.V Singular integral does not exist General integral can be found out in the usual way. Example 1.3b(27): Solve √p + √q = √x. Solution: Given : √p + √q √x … (1) This equation is of the form f (x, p, q) = 0 [Type 3(b)] Assume q = a (constant) We know that, dz = pdx + qdy dz = [x + a - 2 √a √x] dx + ady Integrating on both sides, we get Hence, the complete solution is Since, the number of a.c. = number of I.V Example 1.3b(28) Find the complete integral of q = 2px Solution: Given: q = 2px This equation is of the form f(x, p, q) = 0 Integrating on both sides, we get Hence, the complete solution is Since the number of a.c. = number of I.V [We can solve this easily by Lagrange's idea to get the general integral] EXERCISE 1.3.b [Type 3 Case (ii)] f(x, p, q) = 0 Find the complete integrals of the following : Problems based on Type 3(c) f(y, p, q) = 0 Example 1.3b(29): Solve pq = y. Solution: Given: pq = y ... (1) This equation is of the form ƒ (y,p,q) = 0 [Type 3(c)] Assume p = a (constant) Then aq = y Since, the number of a.c. = number of I.V differentiating p.w.r. to b, we get 0 = 1 (absurd) There is no singular integral differentiating (2) p.w.r. to a, we get Eliminate 'a' between (2) and (3) to get general solution. Example 1.3b(30) : Solve q = py + p2. Solution: Given: q = py + p2 … (1) This equation is of the form f (y, p, q) = 0 [Type 3(c)] Assume p = a (constant) Integrating on both sides, we get differentiating p.w.r. to b, we get 0 = 1 (absurd) There is no singular integral differentiating (3) p.w.r. to a, we get Eliminate 'a' between (3) and (4), we get general solution. EXERCISE 1.3.b [Type 3 Case (iii)] f(y, p, q) = 0 Find the complete solution of the following: Type 4. Separable equations. First order partial differential equations are separable. It can be written as ƒ (x, p) = ϕ (y, q) This equation contains two arbitrary constants and hence it is the complete integral. The singular and general integrals are found out as usual. Problems based on Type 4. Separable equations. Example 1.3b(31): Solve p2y (1 + x2) = qx2. Solution: Given: p2y (1+ x2) = qx2 …(1) The equation is separable This is the complete integral where a and b are arbitrary constants. Differentiating partially w.r.to b, we find that there is no singular integral. Example 1.3b(32) : Find the complete solution of p + q = sin x + sin y. Solution: Given : p + q = sin x + sin y The given differentiating equation can be written as Integrating on both sides z = ax - cosx + (-cos y — ay) + b z = a (x − y) − cos x - cos y + b is the complete integral. [We can solve this easily by Lagrange's idea] Example 1.3b(33) : Find the complete integral of pq = xy. Solution: Given: pq = xy Example 1.3b(34) Find the complete integral of √p + √q = 2x. Solution: Given : √p + √q = 2x The given equation can be written as √p - 2x = - √q This is of the form ƒ (x, p) = ϕ(y, q) Let √p - 2x = -√q = a say Since, the number of a.c. = number of I.V Example 1.3b(35) : Find the complete integral of p-1x+ q-1 y = 1. Solution: Since, the number of a.c. = number of I.V Example 1.3b(36): Solve the equation yp = 2yx + log q. Solution: Given: yp = 2yx + log q yp - 2yx = log q y (p − 2x) = log q where a and b are arbitrary constants equation (3) is the complete solution of the given equation. Since, the number of a.c. = number of I.V differentiating (3) p. w.r.to 'b, we get 0 = 1 [absurd] there is no singular integral. differentiating partially. w.r.to a, we get Eliminate 'a' between (4) and (5), we get the general solution. Find the complete integral of the following: 1.3(3) Equations reducible to standard types: A partial differential equation which is one of the four types. 1. f (p, q) = 0 2. z = px + qy + f (p, q) 3. f (z, p, q) = 0 (or) f(x, p, q) = 0 (or) f (y, p, q) = 0 4. f(x, p) =ϕ (y, q) We will see below a few types of equations, reducible in each case to one of the standard types. III (c) Problems based on equations reducible to standard form: Type 5 Substitute in (1), we get ƒ (P, Q) = 0 [Type 1] Subs.itute in (2), we get f (z, P, Q) = 0 [Type 3] Case (ii) If m = n = 1, then put X = log x, Y = logy Problem based on Type 5 Example 1.3c(1): Solve : x4 p2 + y2 zq = 2z2 Solution: which is the complete integral. Singular and general solutions are found out as usual. Example 1.3c(2) : Solve : p2 + x2y2 q2 = x2z2 Solution: which is the complete integral. Singular and general solutions are found out as usual. Example 1.3c(3): Solve : x2p2 + y2q2 = z2 Solution: Substitute in (2) we get which is the complete integral. The singular and general solutions are found out as usual. Find the complete integral of the following: Type 6 Substitute in equation (1), we get ƒ [P, Q] = 0 [Type 1] Substitute in equation (2), we get f1 (x, P) = f2 (y, Q) [Type 4] Case (ii) If m = -1 then Problem based on Type 6: Example 1.3c(8): Solve. Z2 (p2 + q2) = x2 + y2 Solution : Substitute in equation (1), we get Example 1.3c(9): Solve p2 + q2 = z2 (x2 + y2) Solution : Substitute in equation (1), we get P2 + Q2 = x2 + y2 P2 - x2 = y2 - Q2 This equation is of the form fi (x, P) = f2 (y, Q) Type 4 Example 1.3c(10) : Solve : (zp + x)2 + (żą + y)2 = 1 Solution : Given: (zp + x)2 + (zq + y)2 = 1 …. (1) Substitute in (1), we get This equation is of the form f1 (P, i) |= ƒ2 (Q, y) EXERCISE [Type 6] Find the complete integral of the following:![]() = sin x.
= sin x.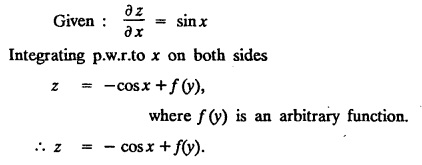
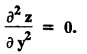
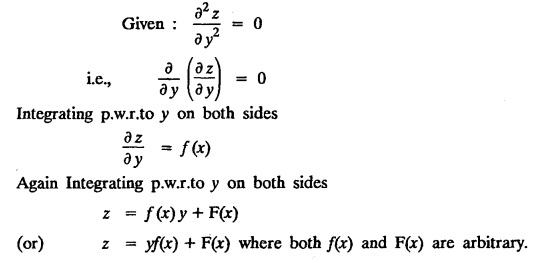
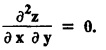
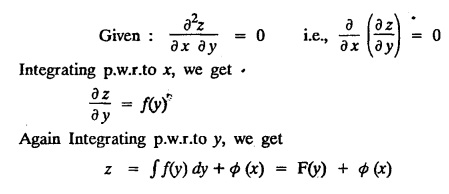
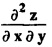 = sin x.
= sin x.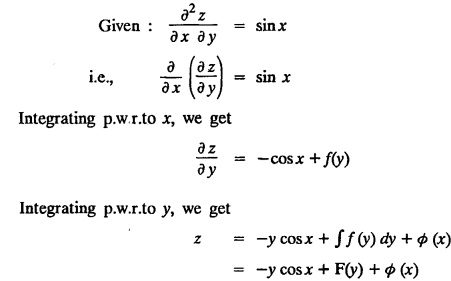
![]() = sin y.
= sin y.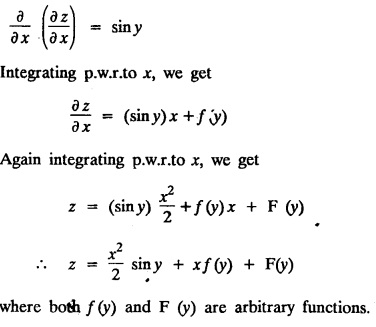
![]() = a2z given that x = 0,
= a2z given that x = 0, ![]() = a sin y and
= a sin y and ![]() = 0.
= 0.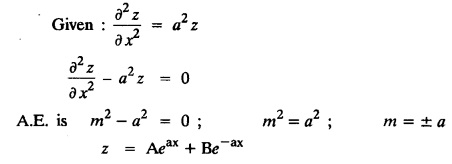
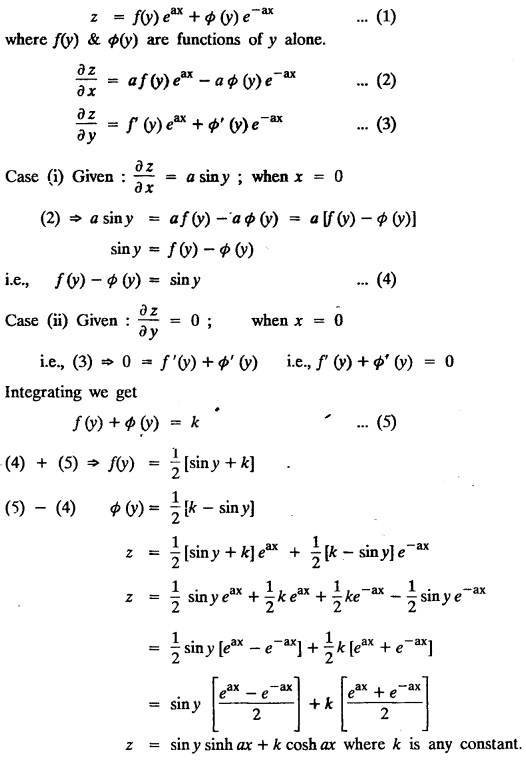
EXERCISE 1.3(a)

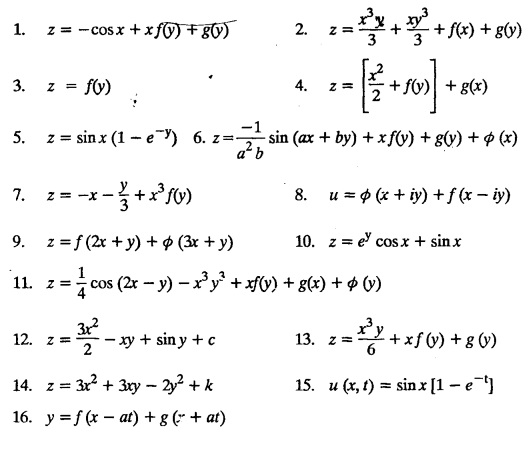
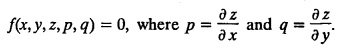
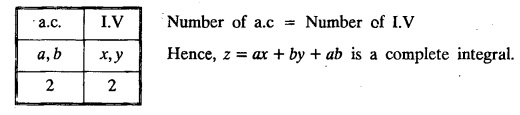
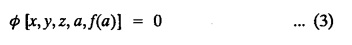
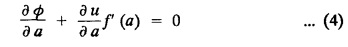


Ill(b) Problems based on First order p.d.e
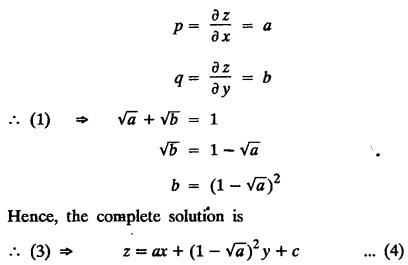
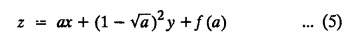
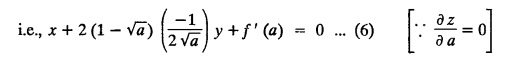
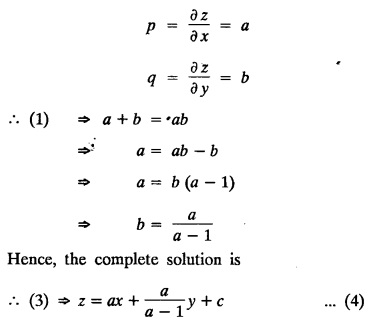
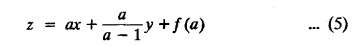
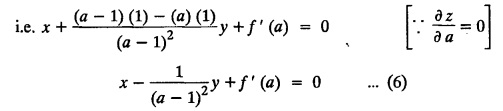
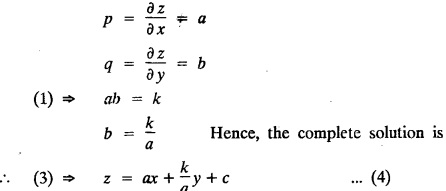
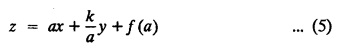
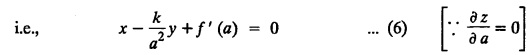
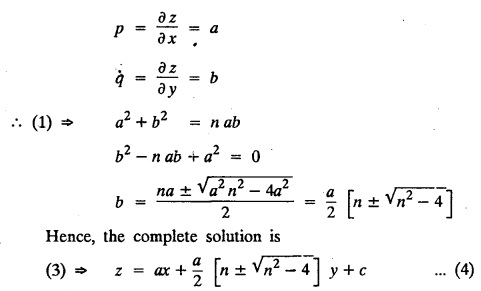
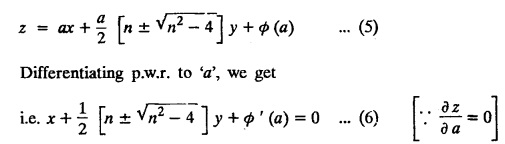
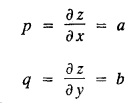
EXERCISE 1.3(b) Type 1.
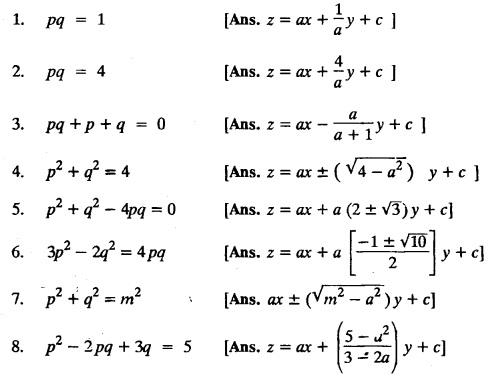
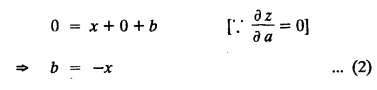
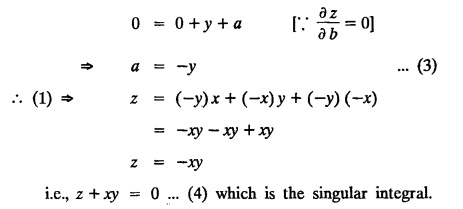
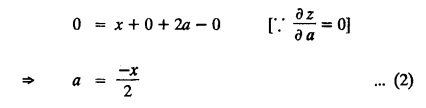
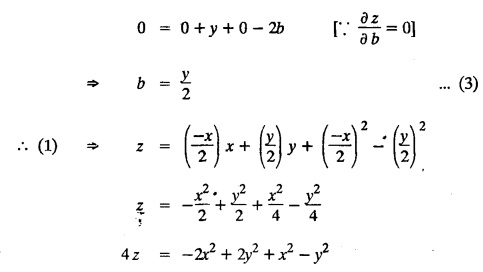
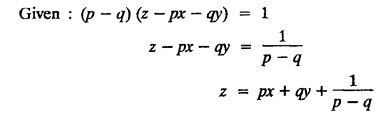
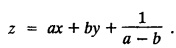
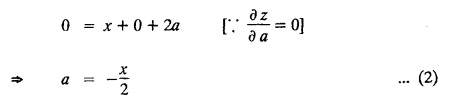
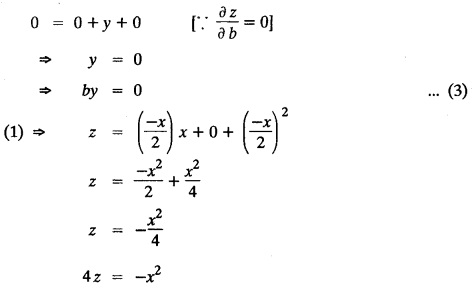
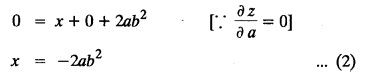

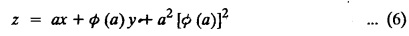
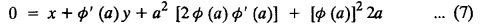
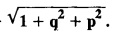
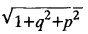
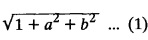
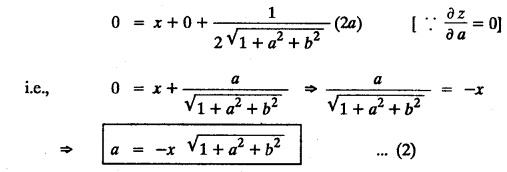

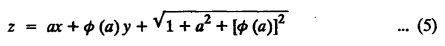
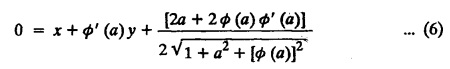
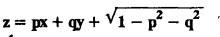
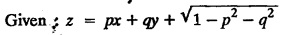
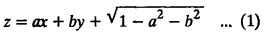
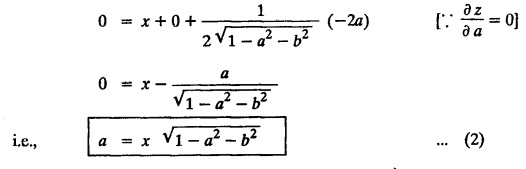

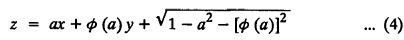
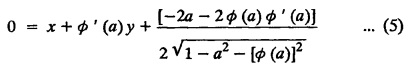
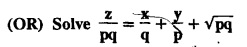
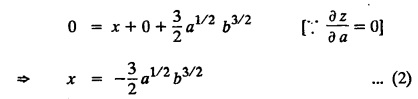

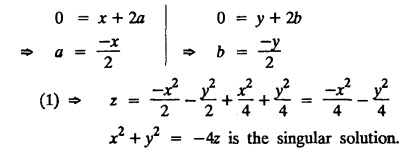
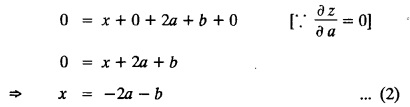

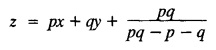
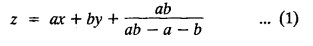
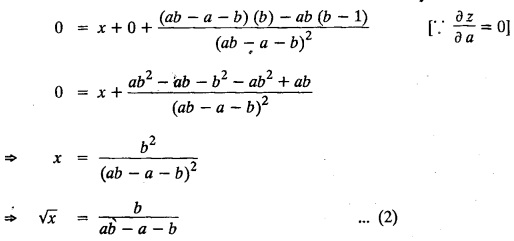

EXERCISE 1.3(b) [Type 2]


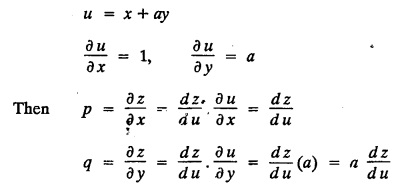
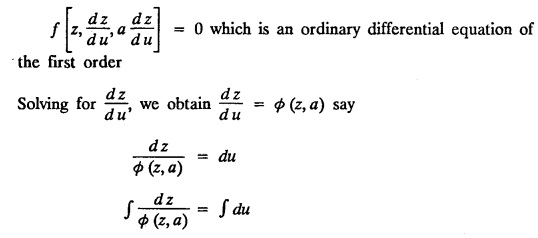
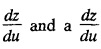 in the given equation and then solve the ordinary diff. Equation obtained.
in the given equation and then solve the ordinary diff. Equation obtained.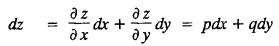
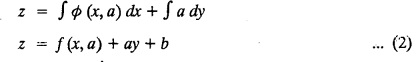

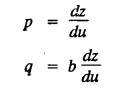
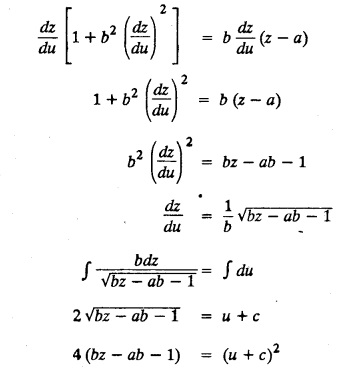
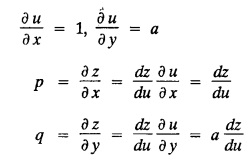
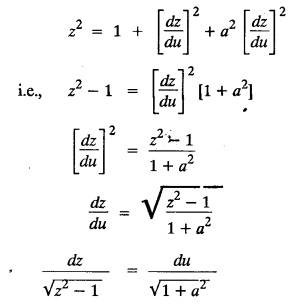
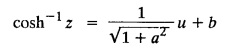
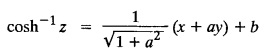
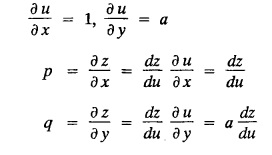
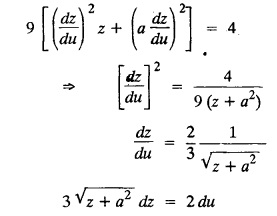
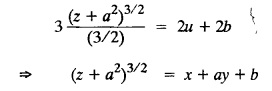
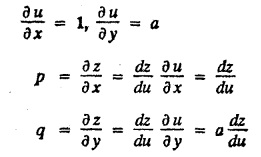
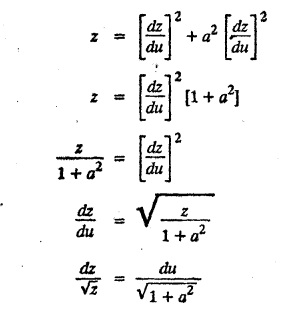
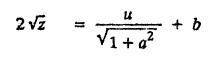
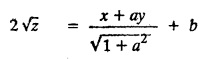
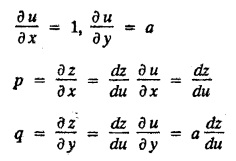
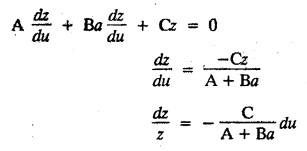
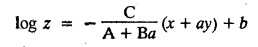
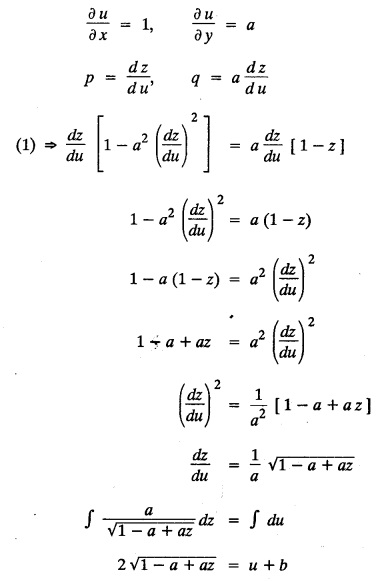
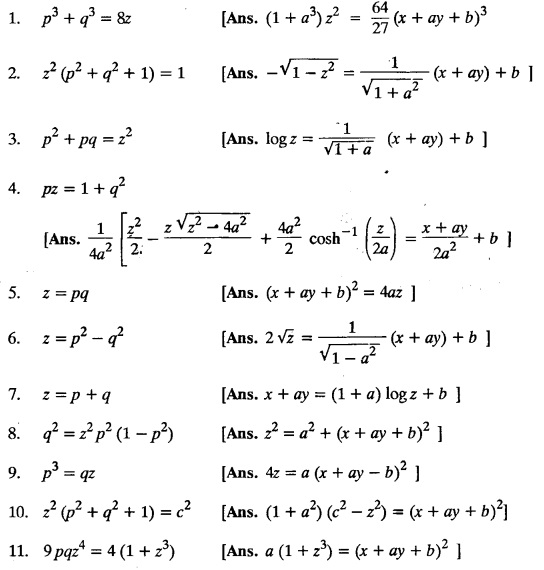
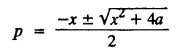
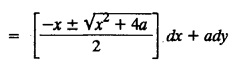
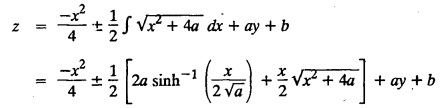
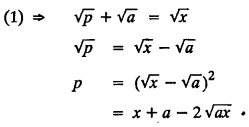
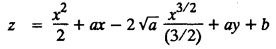
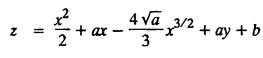
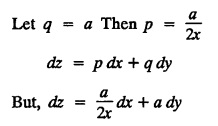
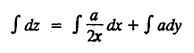
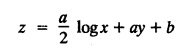
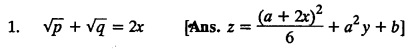
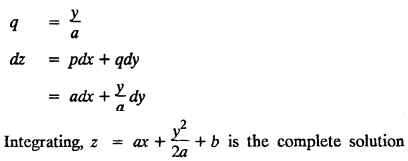
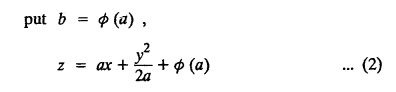
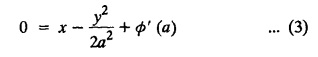
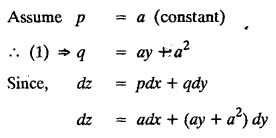
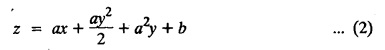
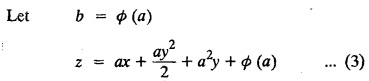
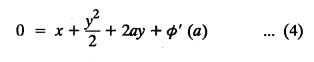
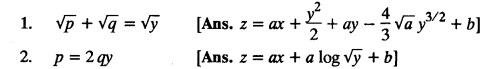
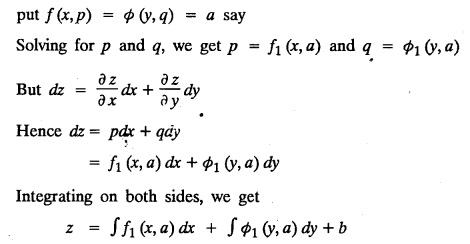

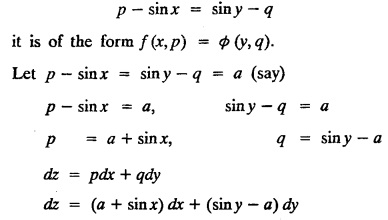

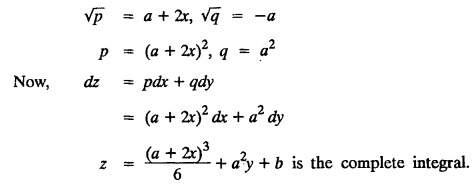
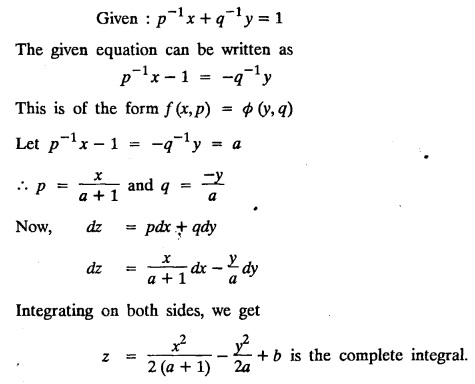
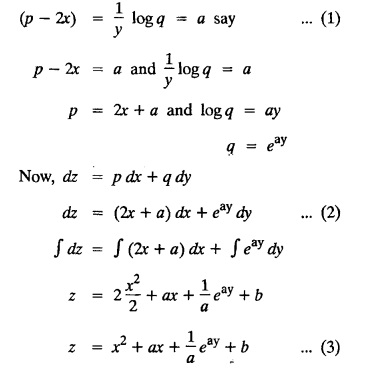
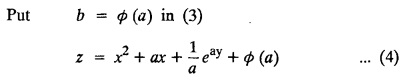
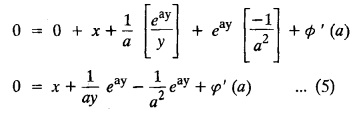
EXERCISE 1.3.b [Type 4]
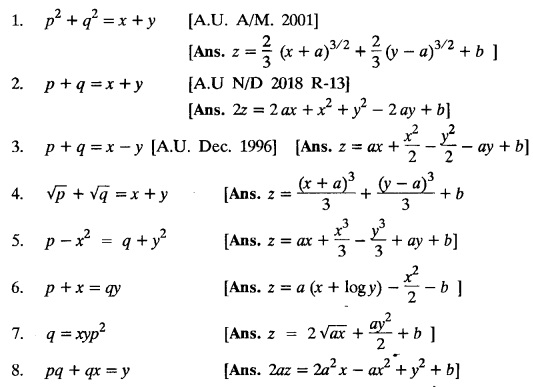
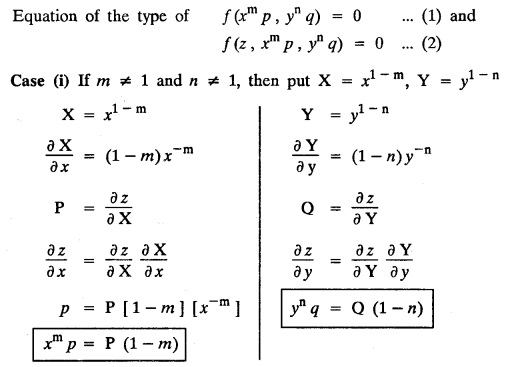
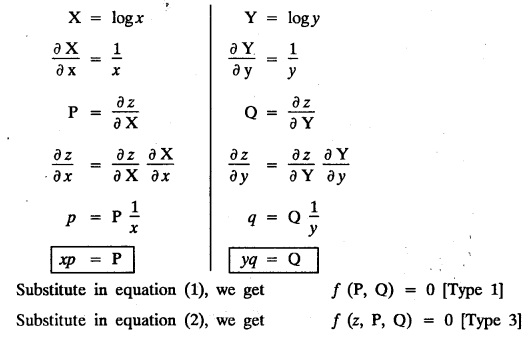
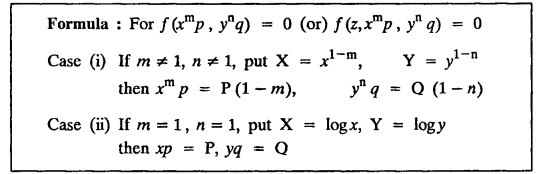

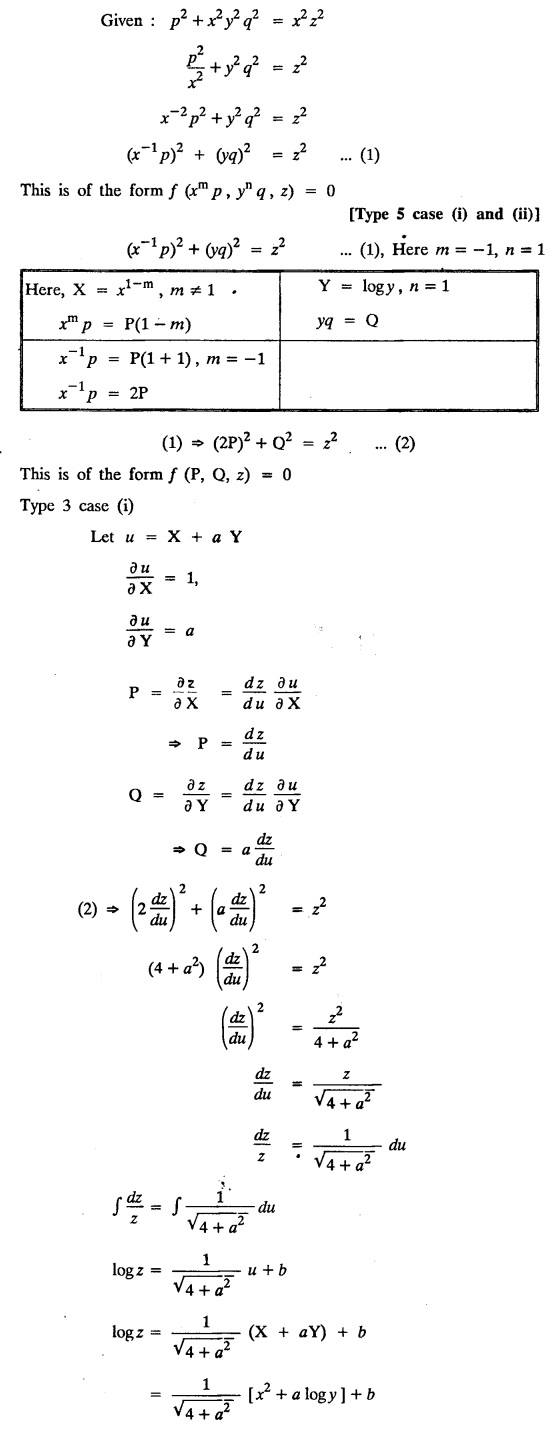
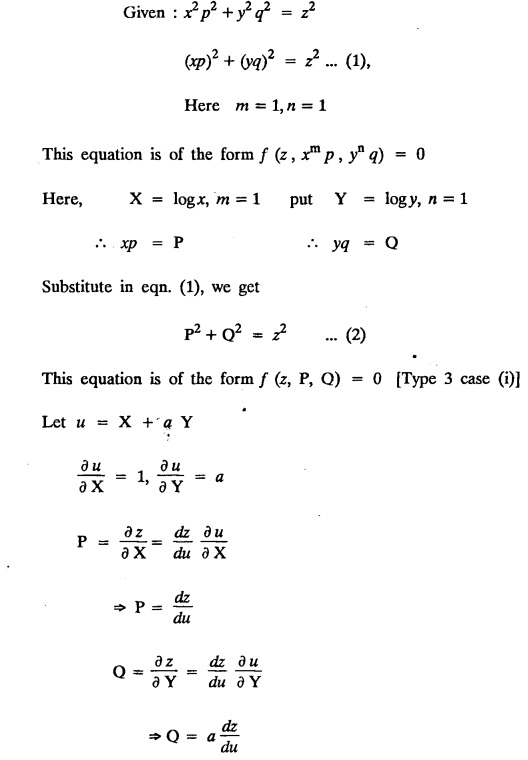
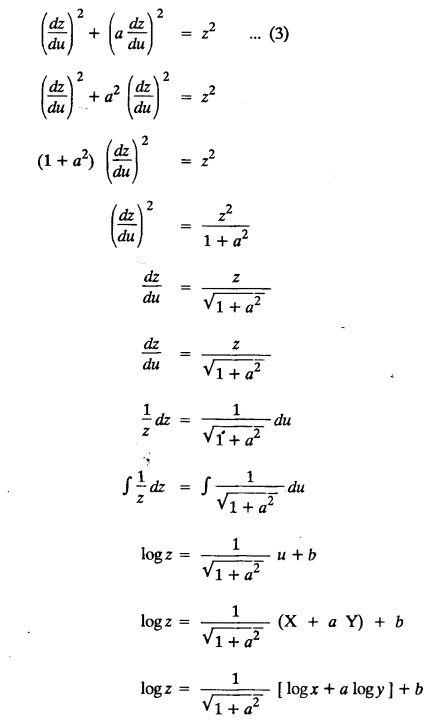
EXERCISE 1.3.c
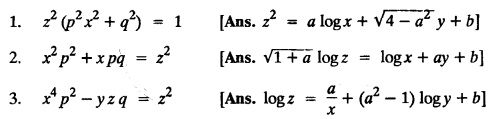

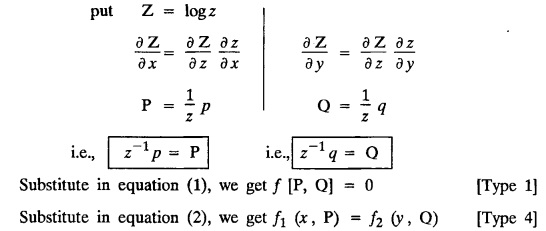
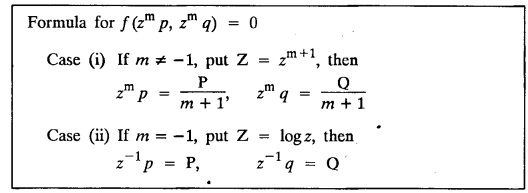
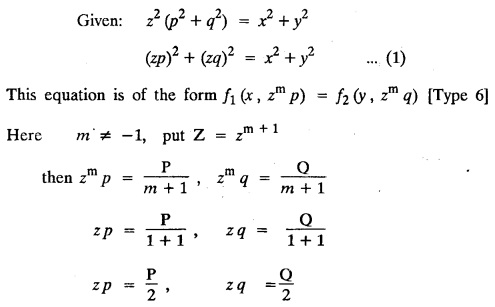
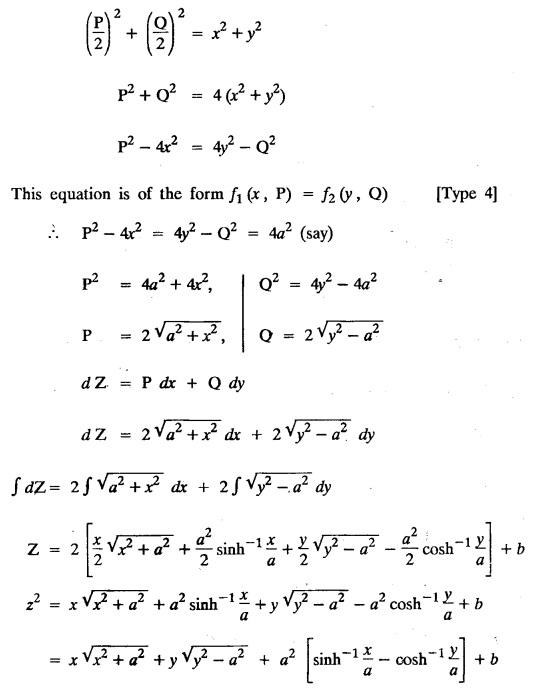
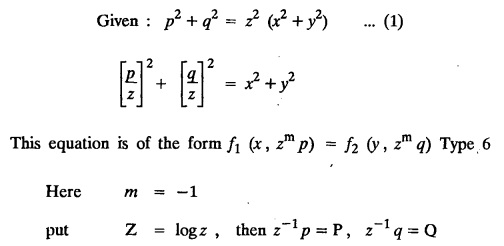
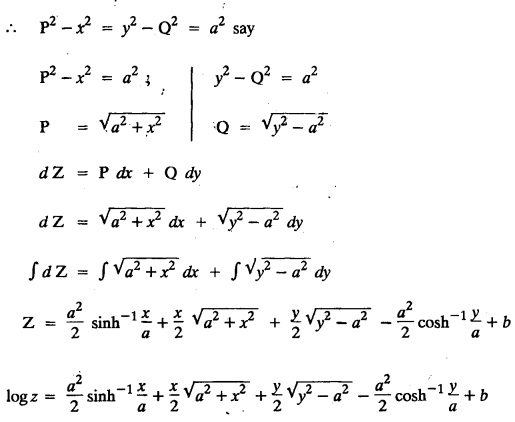
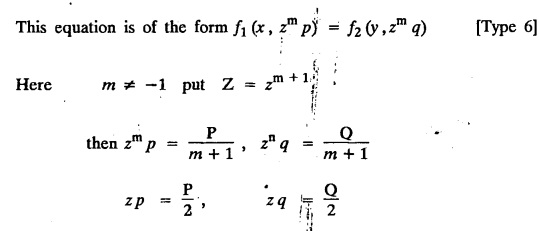
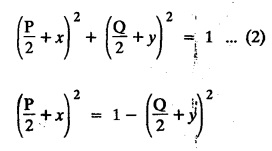
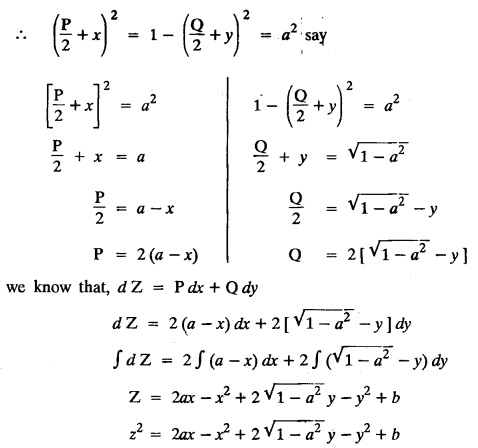
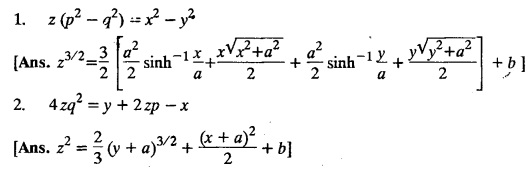
Transforms and Partial Differential Equations: Unit I: Partial Differential Equations : Tag: : Solved Example Problems - Singular integrals grals - solution of standard types of first order partial differential equations
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
