Engineering Physics: Unit III: a. Oscillations
Simple Harmonic Motion
Definition, Characteristics, Example, Types
An oscillatory motion is harmonic if the displacement can be expressed in terms of sine or cosine function. An oscillator executing harmonic motion is called a harmonic oscillator.
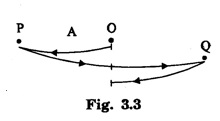
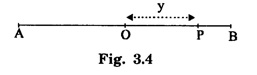
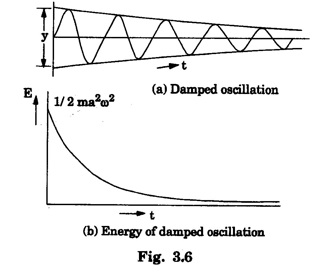
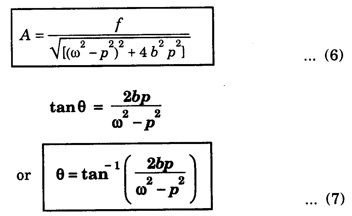
SIMPLE HARMONIC MOTION An oscillatory motion is harmonic if the displacement can be expressed in terms of sine or cosine function. An oscillator executing harmonic motion is called a harmonic oscillator. When the acceleration of particle is directly proportional to its displacement from its equilibrium position and it is always directed towards equilibrium position, then the motion of the particle is said to be simple harmonic motion. A particle executing simple harmonic motion must satisfy the following conditions: • The motion must be periodic. • The motion is oscillatory ie., to and fro along a straight line or along a curved path about a mean position. • The body executing simple harmonic motion is acted upon by a restoring force whose magnitude is proportional to the displacement and its direction is always towards the mean position. • If there is no air resistance or friction, the motion once started will continue indefinitely. • Simple Pendulum It consists of an ideally massless inextensible string hanging from a rigid support A with a point mass (i.e., the bob of the pendulum) connected to its other end B. This is shown in fig. 3.1. When the bob is displaced to a new position P and released, oscillations start and it is in simple harmonic motion. If θ is the angle made by the string at P with the equilibrium condition of the string AB, m and g are the mass of the bob and the acceleration due to gravity, then the radial component of mg (i.e., mg cos θ) balances the tension T across the string. The tangential component 'mg sin θ' tries to bring the bob at B. These way oscillations continue till it stops due to air friction. ● Spring - Mass system Here a mass block is connected to a spring either vertically or horizontally from rigid supports as shown in fig.3.2 (a) and (b). On displacing the mass from its equilibrium position and then releasing it, again simple harmonic oscillations set in. ● Vibrations of a tuning fork. ● Vibrations of a sonometer wire. ● Vertical oscillations of the liquid column in a U-tube. ● Angular oscillations of a torsion pendulum. The simple harmonic motions are of two types: (i) Linear Simple Harmonic Motion If the displacement of a particle executing S.H.M. is linear, the motion is said to be linear S.HM. The examples of linear S.H.M. are motion of simple pendulum, the motion of prongs of vibrating tuning fork, the motion of a point mass attached to a spring. (ii) Angular Simple Harmonic Motion If the displacement of a particle executing S.H.M. is angular, the motion is said to be angular S.H.M. The example of angular S.H.M. is torsional oscillations of a solid. If α is linear acceleration and y is displacement from equilibrium position, then essential condition for linear S.H.M. is If α is angular acceleration and θ angular displacement from equilibrium position, then essential condition for angular S.H.M. is Let a particle execute S.H.M along straight line QOP, about O. (Fig. 3.3) 1. Amplitude The maximum displacement of a particle from mean position is called the amplitude. It is denoted by A. Then, OP = OQ = A. 2. Oscillation When particle moves from mean position O from P, returns P to Q via O and then comes back from Q to O; then particle is said to complete one-oscillation i.e., 1 oscillation = motion from O to P + from P to from Q + from to Q to O or motion (from P to Q + from Q to P) 3. Period The time taken by the particle executing S.H.M to complete one oscillation is called the period or periodic time. It is denoted by T. 4. Frequency The number of oscillations completed by particle in one second is called its frequency. It is denoted by n Frequency n = 1/period (T) 5. Phase The position and direction of motion of a vibrating particle is different at different instants. The instantaneous position and direction of motion of a vibrating particle is expressed by a physical quantity called the phase. If S.H.M is expressed as y = A sin (ω t + ϕ); then quantity (ω t + ϕ) is the phase of vibrating particle. A particle executing S.H.M is called a harmonic oscillator. Consider a particle of mass m executes S.H.M. along a straight line (Fig. 3.4). Let y be the displacement of particle from mean position at any time t. On basic condition of S.H.M. the restoring force F proportional to displacement y and oppositely directed i.e., where k is a constant of proportionality and it is called spring factor or force constant. Its unit is newton / metre (N/m). If where The eqn. (3) represents the differential equation of SHM. A general solution of the differential equation for SHM is given by where A is the amplitude of the SHM. ϕ is the initial phase. Now consider a particle executing angular harmonic motion. At any instant t, let θ be the angular displacement measured from the equilibrium position of the particle. Then, similar to equation (3) for the linear case, we have Torsional oscillations of a stretched wire, oscillations of a freely suspended bar magnet in a magnetic field etc. are examples of angular harmonic motion. We have displacement y = A sin (ω t + ϕ) Differentiating with respect to time t, we get Equation (7) gives velocity of particle at any displacement y. Maximum velocity is obtained by putting y = 0. Thus, velocity is maximum and equal to Aω at mean position and velocity is zero at y = ± A (extreme positions). Differentiating eqn (6) with respect to time t, Equation (8) gives acceleration of oscillating particle at any displacement y from the mean position. This equation is the standard equation of S.H.M. For maximum acceleration at y = A (extreme position) ⸫ Maximum acceleration, amax = ω2 A (at extreme position) Minimum acceleration is obtained by putting y = 0 ⸫ amin = 0 (at mean or equilibrium position). The time taken by the particle to make one complete to and fro motion is called the time period of the S.H.M. It is also equal to the time required by the particle to trace an angle 2π. Since ω is the uniform angular velocity. From eqn (8), we have Substituting this in eqn. (9), we have Let n be the frequency of the S.H.M, i.e., number of oscillation made by the particle in one second. But, period = Time taken for one oscillation. From eqns. (10) and (11), we have There are three types of oscillations. They are 1. Free oscillations 2. Damped oscillations 3. Forced oscillations When a body is displaced from its equilibrium position and then released, it oscillates under the influence of restoring force with a definite frequency i.e., natural frequency. (Fig. 3.5) Such vibrations are called free vibrations. The frequency of such vibration is known as natural frequency. The frequency of vibration depends only on geometric dimensions of the body and its elastic property Examples 1. Vibrations in a stretched string 2. A tuning fork struck against a rubber pad 3. Oscillation of a simple pendulum. Characteristics of free vibration (i) Amplitude of oscillation is a constant (Fig. 3.5) (ii) Frequency depends on geometric dimensions and elastic property. (iii) No dissipation of energy Most of the oscillations occur in air or in a medium. Hence, the medium offers some resistive force on the oscillating body. So, a part of the energy is dissipated in overcoming the resistive forces. Consequently the amplitude of oscillation goes on decreasing exponentially with time and finally becomes zero. Such oscillations are called damped oscillations (Fig.3.6(a)). As a result the energy of oscillations decreases with time (Fig.3.6(b)). Characteristic of a damped oscillation (i) Amplitude of oscillation is not a constant (ii) There is dissipation of energy (iii) Small changes are produced in the frequency of oscillation Example The oscillations of a pendulum in air. If some external periodic force is constantly applied on a system of damped oscillations, it is possible to compensate the energy it has lost. Therefore, the system continues to oscillate or vibrate with a constant amplitude. When a body A is maintained in the state of vibration by a periodic force of frequency v other than its natural frequency (v0) of the body, the vibrations are called forced vibrations Then the body A will vibrate with v and not with v0, such vibrations are called forced vibrations. External force is the driver and the body A is driven. Characteristics of forced oscillations are (i) Amplitude will be a constant (ii) The frequency of forced vibration is equal to that of the external periodic force. (iii) The amplitude of the forced vibration is determined by the frequency of the applied force and the natural frequency Examples 1. Press the stem of a vibrating tuning fork, against tabla. The tabla suffer forced vibrations 2. Sound boards of stringed instruments suffer forced vibrations. 3. Swing can be kept in motion by giving constant periodic forces. Hence the swing maintains its amplitude while oscillating. Consider a particle of mass m connected to a spring (Fig. 3.7). This particle is driven by a periodic force. The oscillations are started and the forces acting on the particles are (i) a restoring force. It is proportional to the displacement acting in the opposite direction. It is given by - ky where k is known as the restoring force constant. (ii) a frictional force. It is proportional to velocity but acting on the opposite direction. It is given by Therefore, net force F' acting on the particle By Newton's second law of motion, the resultant force acting on the particle F = mass × acceleration = ma The eqn. (4) is the differential equation of the motion of the forced oscillation of the particle. The solution of differential eq. (4) where A is the steady amplitude of vibrations We have The equation (6) gives the amplitude of forced vibration while eqn (7) its phase. It is clear that the amplitude and phase of the forced oscillations depend upon (ω2-p2), ie., they depend upon the driving frequency (p) and the natural frequency of the oscillator (ω).Definition
Characteristics of simple harmonic motion
Example for simple harmonic motion
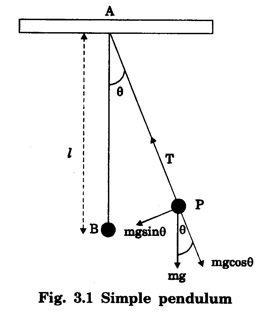
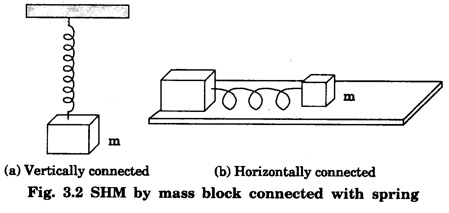
Types of Simple Harmonic Motion (S.H.M)
Essential conditions for S.H.M
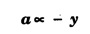
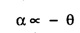
Definitions concerning S.H.M
Differential Equation of S.H.M

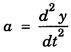 is acceleration at any instant t, then by Newton's second law of motion F = mass × acceleration = ma
is acceleration at any instant t, then by Newton's second law of motion F = mass × acceleration = ma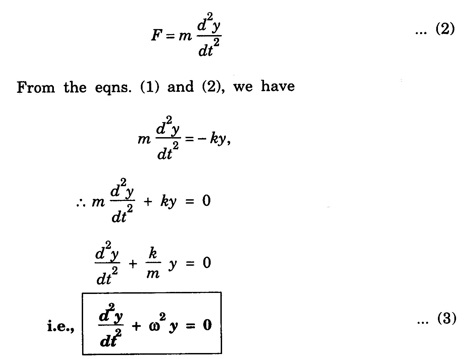
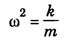 is a constant and w is known as angular frequency
is a constant and w is known as angular frequency
Angular harmonic motion
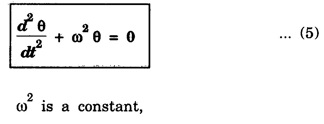
Velocity and Acceleration
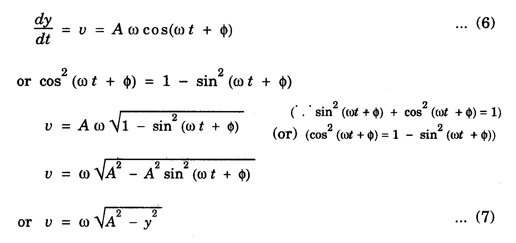
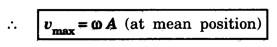
Acceleration
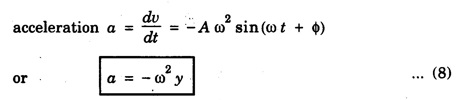
Period of S.H.M
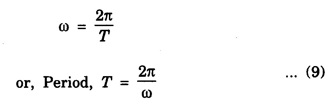
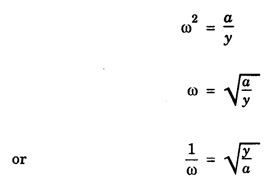


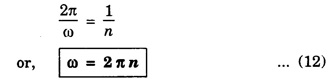
Types of oscillations
(a) Free oscillation
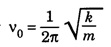
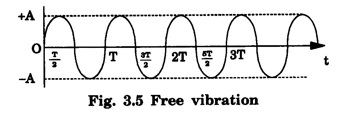
(b) Damped oscillation
(c) Forced vibration
Differential Equation for Forced Oscillations
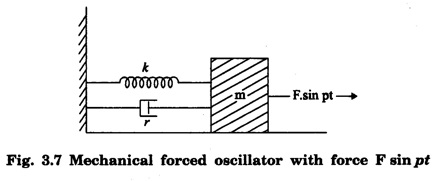
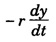 where r is the frictional force constant. (iii) the external periodic force, F sin pt where F is the maximum value of the force and p is its angular frequency. This force opposes the restoring force as well as the frictional force and helps in motion.
where r is the frictional force constant. (iii) the external periodic force, F sin pt where F is the maximum value of the force and p is its angular frequency. This force opposes the restoring force as well as the frictional force and helps in motion.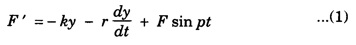
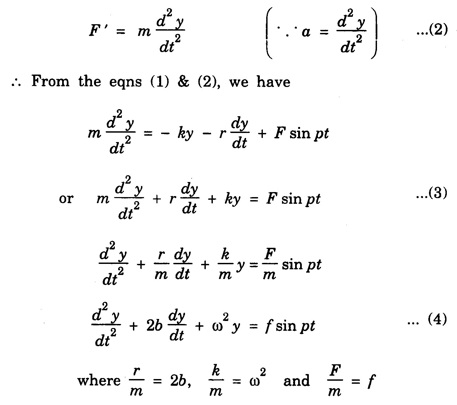

Engineering Physics: Unit III: a. Oscillations : Tag: : Definition, Characteristics, Example, Types - Simple Harmonic Motion
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
