Theory of Machines: Unit II: Gears and Gear Trains
simple gear train
Gears and Gear Trains - Theory of Machines
When there is only one gear on each shaft, it is known as simple gear train.
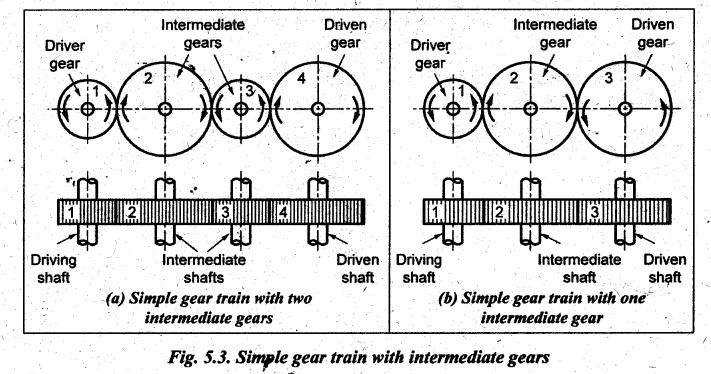
SIMPLE GEAR TRAIN • When there is only one gear on each shaft, it is known as simple gear train. • A simple gear train is shown in Fig.5.2. • As shown in Fig.5.2, the gear 1 drives the gear 2, therefore gear 1 is called the driver and the gear 2 is called the driven or follower. • It can be seen that the motion of driven gear is opposite to the motion of driving gear. Let N1 = Speed of driving gear in rpm, N2 = Speed of driven gear in rpm, d1 = Pitch circle diameter of driving gear, d2 = Pitch circle diameter of driven gear, Τ1 = Number of teeth on driving gear, and T2 = Number of teeth on driven gear. We know that the pitch line velocity (ie., peripheral velocity) at the point of contact of two mating gears will be equal. i.e., Pitch line velocity of gear 1 = Pitch line velocity of gear 2 Also pitch (p) of both mating gears are same. From equations (i) and (ii), we get In equation (5.2), the negative sign indicates that the driver and driven gears are rotating in the opposite direction. • Intermediate gears, also known as idler gears, are necessary: (i) to change the direction of rotation of the driven gear without changing its angular velocity, and (ii) to bridge the gap between first and last gears, when the centre distance is large. • Fig.5.3(a) shows a simple gear train with two intermediate gears. In Fig.5.3(a), gears 2 and 3 are intermediate gears which serve to bridge the gap between the first and last gears. • From Fig.5.3, it can be seen that • The direction of rotation of both the driver and the driven gears is opposite, when the number of intermediate gears is even (see Fig.5.3(a)). • The direction of rotation of both the driver and the driven gears is same, when the number of intermediate gears is odd (see Fig.5.3(b)). 1. Effect of Number of Intermediate Gears on Train Value Consider Fig.5.3(a) where a simple gear train with two intermediate gears are shown. Let N1, N2, N3 and N4 = Speeds of gears 1, 2, 3 and 4 respectively, and T1, T2, T3 and T4 = Number of teeth on gears 1, 2, 3 and 4 respectively. Multiplying equations (i), (ii) and (iii), we get Hence, it is clear from the above equation that the train value is independent of the size and number of intermediate gears. They do not affect the train value and that's why these intermediate gears are called idler gears.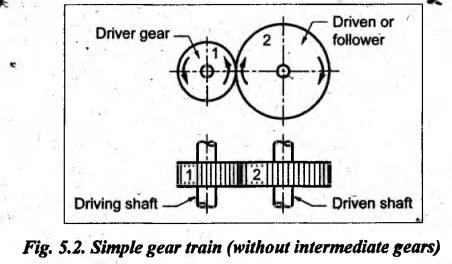
1. Train Value of a Simple Gear Train
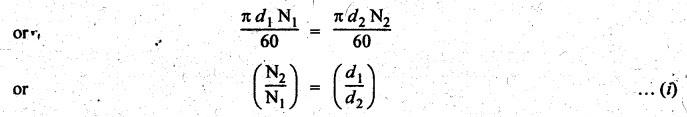
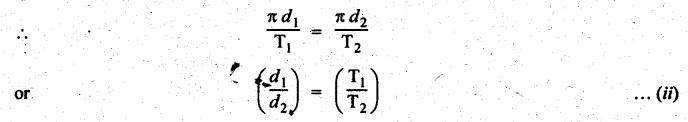
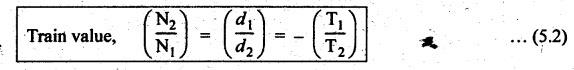
2. Simple Gear Train with Intermediate Gears
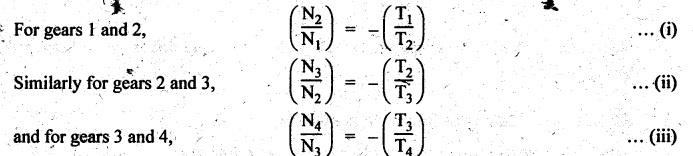
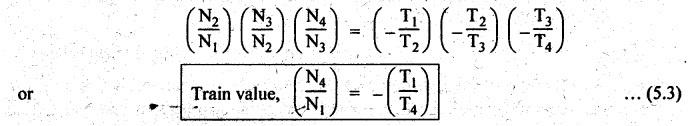
Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - simple gear train
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
