Engineering Graphics: Unit IV (a): Sections of Solids
Sections of sphere
Construction, Steps, Example Problems | Engineering Graphics (EG)
When a sphere is cut by a horizontal plane the section will be a circle.
SECTIONS OF SPHERE When a sphere is cut by a horizontal plane the section will be a circle. Similarly if the sphere is cut by a vertical plane the section will be a circle of same diameter. Hence only the other two types of sections are dealt in this article. Example 34 : A sphere of 60 mm diameter is kept on HP. It is cut by a plane, inclined at 45° to HP and perpendicular to VP. The section plane passes through the sphere at a distance of 15 mm from the centre of the sphere and above it. Draw the front view, sectional top view and true shape of the section. Step 1 (Top view): Draw the reference axis XY and draw a circle of diameter 60 mm as the top view. Step 2 (Front view): Project the top view and obtain another circle of 60 mm diameter as front view. Step 3 (True shape of section): The cutting plane is inclined to HP. Hence draw V.T of cutting plane in front view at an angle of 45° to XY and 15 mm away from the centre of sphere. (To draw V.T, a circle may be drawn of 15 mm radius with centre O' and draw a tangent to the circle inclined at 45° to XY). Draw another axis X1Y1 at any convenient distance and parallel to the cutting plane. Draw a line parallel and equal to V.T and keeping this line as the diameter draw a circle and divide the circumference of circle into 8 equal parts. Hatch the circle which represents the true shape of the section. Name the points on circumference as a1, b1, c1 etc., Step 4 (Sectional top view): Draw the projectors from the points a1, b1, c1 etc. in true shape perpendicular to the cutting plane, to intersect at a', b', c' etc., respectively. Project the points a', b', c' etc. to the top view and obtain the points a, b, c etc. such that their distances from XY are equal to the respective distances of a1, b1, c1 etc. from X1Y1. Join the points a, b, c etc. in sequence and hatch the area enclosed, which represents the sectional top view. Example 35: A sphere of 60 mm diameter is on HP and cut by a plane inclined at 45° to VP and parallel to HP, at a distance of 10 mm from the centre of the sphere and the portion between the observer and cutting plane is removed. Draw the top view, sectional front view and true shape of the section. The true shape of a sphere at any position of cutting plane is a circle. Hence it is suggested to draw the true shape of section as a circle and then project it for the sectional front view. This problem is similar to the previous problem, but draw H.T of cutting plane in top view. Draw the top view first, then draw the front view as a circle. Draw the cutting plane and complete the true shape of section, then finally draw the sectional front view. The projections are shown in Fig. 15.46.1. Section of sphere cut by a plane inclined to HP and perpendicular to VP
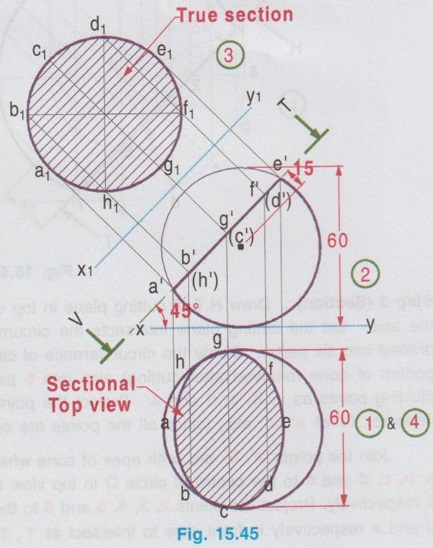
2. Section of sphere cut by a plane inclined to VP and parallel to HP
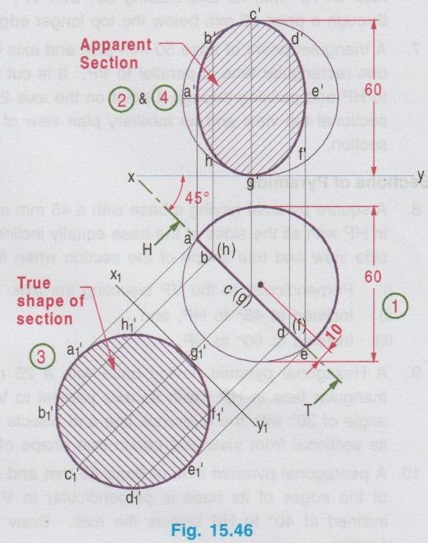
Engineering Graphics: Unit IV (a): Sections of Solids : Tag: : Construction, Steps, Example Problems | Engineering Graphics (EG) - Sections of sphere
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
