Engineering Graphics: Unit IV (a): Sections of Solids
Sections of pyramids
Construction, Steps, Example Problems | Engineering Graphics (EG)
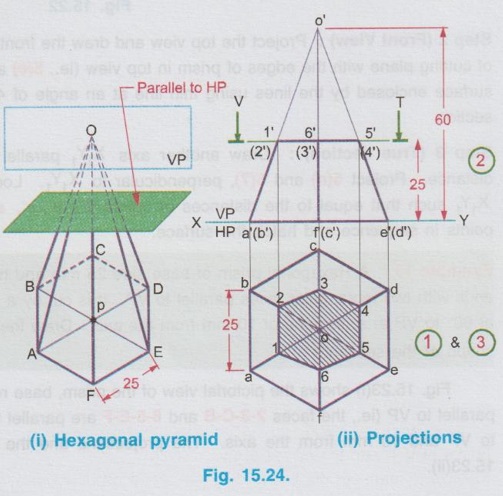
A Hexagonal pyramid of base side 25 mm and altitude 60 mm rests on its base on HP with two edges of the base perpendicular to VP.
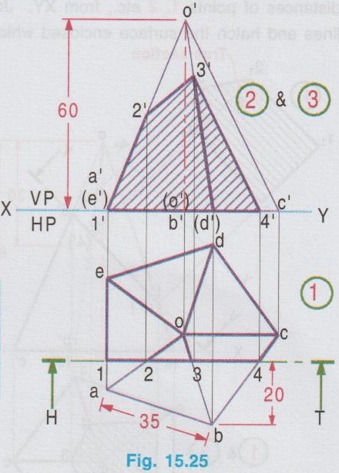
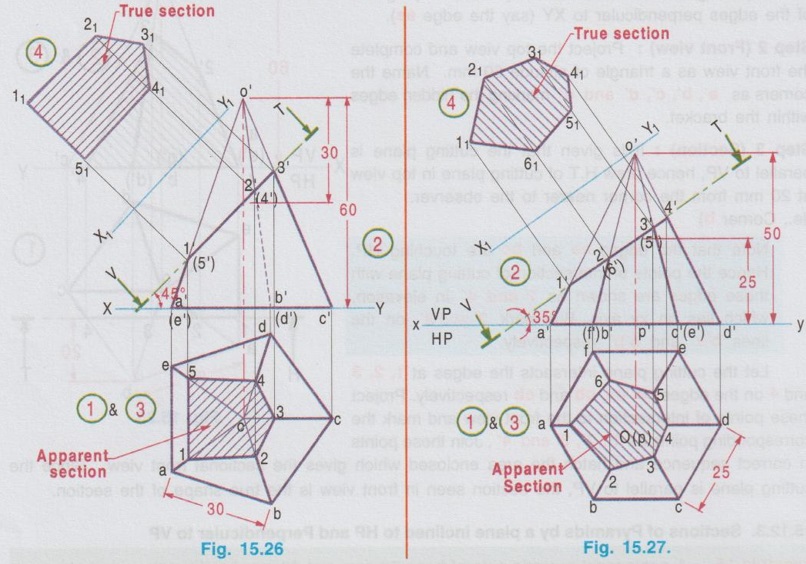
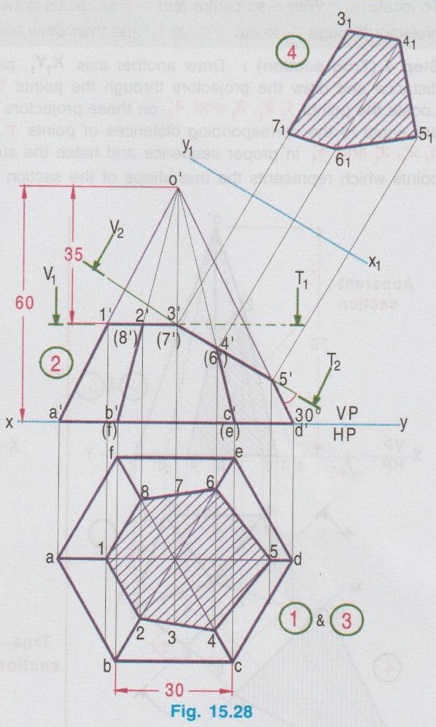
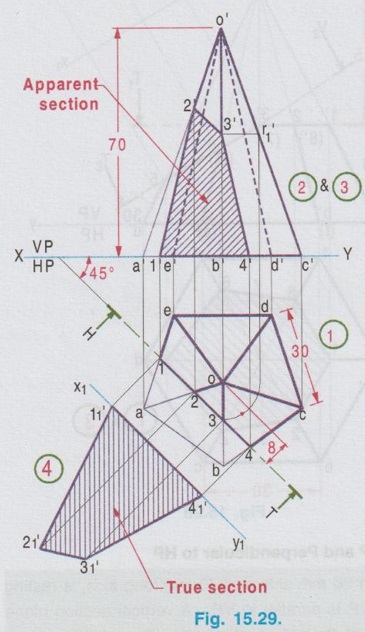
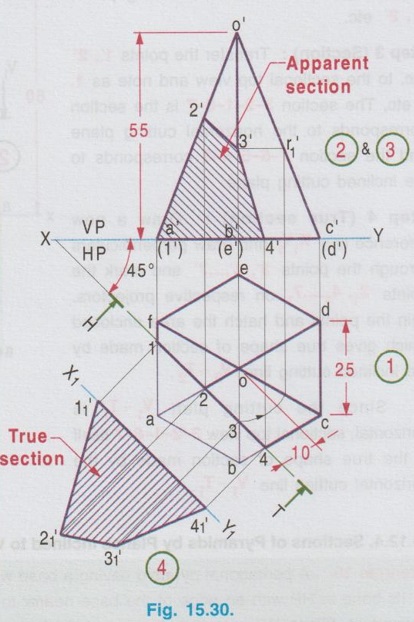
SECTIONS OF PYRAMIDS Example 14: A Hexagonal pyramid of base side 25 mm and altitude 60 mm rests on its base on HP with two edges of the base perpendicular to VP. A cutting plane parallel to HP cuts the pyramid at a height of 25 mm above ells the base. Draw the front view and theol sectional view. Fig. 15.24 (i) shows the hexagonal pyramid, the corners named as A, B, C, D, E, F and the axis OP with the edges AB and DE perpendicular to VP. The projections of the pyramid for the given position of cutting plane are shown in Fig. 15.24 (ii). Example 15: A pentagonal pyramid side of base 35 mm and axis 60 mm long, rests with its base on HP such that one of the edges of the base is perpendicular to VP. A section plane perpendicular to HP and parallel to VP cuts the pyramid at a distance of 20 mm from the corner of the base nearer to the observer. Draw the top view and sectional front view. Step 1 (Top view): Draw the reference line XY and draw a pentagon of side 35 mm as top view, keeping one piw betons coste dolari bns senil of the edges perpendicular to XY (say the edge ae). Step 2 (Front view): Project the top view and complete the front view as a triangle of altitude 60 mm. Name the corners as a', b', c', d' and e' marking the hidden edges within the bracket. Step 3 (Section): It is given that the cutting plane is parallel to VP, hence draw H.T of cutting plane in top view at 20 mm from the corner nearer to the observer. (ie., Corner b) Note that the edges ae and bc are touching HP. Hence the points of intersection of cutting plane with these edges are shown as 1' and 4' in elevation, which lies on xy axis. But mark 2′ and 3′ on the lines o'a' and o'b' respectively. Let the cutting plane intersects the edges at 1, 2, 3 and 4 on the edges ae, oa, ob and cb respectively. Project these points of intersection to the front view and mark the corresponding points as 1', 2', 3' and 4'. Join these points in correct sequence and hatch the area enclosed which gives the sectional front view. Since the cutting plane is parallel to VP, the section seen in front view is the true shape of the section. Example 16: A pentagonal pyramid side of base 30 mm and 60 mm height rests with its base on HP. One of the edges of its base is perpendicular to VP. A section plane perpendicular to VP and inclined at 45° to HP bisects the axis. Draw the sectional top view and front view. Also draw the true shape of the section. Step 1 (Top view) : Draw a pentagon of side 30 mm as top view keeping one of the edges perpendicular to XY. (say the edge ae) Step 2 (Front view): Project the top view and complet the front view. Name the corners as a', b' etc., showing the hidden points within the bracket. Step 3 (Section): Draw V.T of cutting plane in front view, at an angle of 45° to XY, cutting the axis in such a way that it bisects the axis. ie., at 30 mm from the apex. Assume that the portion of pyramid above V.T is removed and darken the remaining portion of pyramid. Mark the intersecting points of V.T with the edges of pyramid as 1', 2', 3', 4' and 5' in front view. Project these points to topview to intersect the line joining the centre and the corresponding corner at 1, 2, 3, 4 and 5. Join these points in a sequence using thick lines and hatch the area enclosed using thin lines at an angle of 45° which represents the apparent shape of the section. Step 4 (True shape of section): Draw another axis X1Y1 parallel to the cutting plane at any convenient distance. Project the points from front view, perpendicular to the axis X1Y1. Locate the points 11, 21 etc., in such a way that their distances from X1Y1 are equal to the corresponding distances of points 1, 2 etc., from XY. Join the points 11, 21 etc., in proper sequence using thick lines and hatch the surface enclosed which represents the true shape of the section. Example 17: A Hexagonal pyramid side of base 25 mm and altitude 50 mm rests with its base on HP and with two sides of base, parallel to VP. It is cut by a cutting plane inclined at 35° to HP and perpendicular to VP and is bisecting the axis. Draw the front view, sectional plan and true shape of the section. The projections are shown above in Fig. 15.27. Example 18: A Hexagonal pyramid of base side 30mm and altitude 60mm rests on its base on the HP with two base edges parallel to the VP. It is cut by a horizontal plane perpendicular to the VP meeting the axis of the pyramid at 35mm from the vertex. The pyramid is also cut by an another plane perpendicular to the VP and inclined at 30° to the HP, meeting the axis at the point where the horizontal plane meets the axis. Draw the front view, sectional top view and true section. This problem is a combination of Examples 14 and 17, subjected to a horizontal plane and an auxiliary plane. Step 1 (Top view): Draw the top view as a hexagon keeping two sides parallel to VP. Step 2 (Front view): Project the top view above XY line and draw the front view. Let V1T1 be the horizontal cutting plane drawn at 35mm below vertex and V2T2 be the inclined cutting plane at 30° to HP meeting the axis at the same point. Mark the cutting points 1', 2' etc. Step 3 (Section): Transfer the points 1', 2' etc. to the sectional top view and note as 1, 2 etc, The section 3-2-1-8-7 is the section corresponds to the horizontal cutting plane and the section 7-6-5-4-3 corresponds to the inclined cutting plane. Step 4 (True section) : Draw a new reference line X1Y1 and draw perpendiculars through the points 3', 4'....7' and mark the points 31, 41,…71 on respective projectors. Join the points and hatch the area enclosed which gives true shape of section made by the inclined cutting line V2 - T2. Since the cutting plan V1 – T1 is horizontal, sectional top view 3-2-1-8-7 itself is the true shape of section made by the horizontal cutting line V1- T1. Example 19: A pentagonal pyramid having a base with 30 mm side and 70 mm long axis, is resting on its base in HP with an edge of the base nearer to VP is parallel to VP. A vertical section plane inclined at 45° to VP cuts the pyramid at a distance of 8mm from the axis. Draw its top view, sectional top view and true shape of the section. Step 1 (Top view): Draw a pentagon of side 30 mm as top view keeping the edge nearer to VP is parallel to it. Name the corners as a, b, c, d and e. Step 2 (Front view): Project the top view to complete the front view and name the corresponding points as a', b' etc., Step 3 (Section): The cutting plane is inclined at 45° to VP. Hence draw H.T of the cutting plane in top view inclined at 45° to XY and 8 mm from the axis. Project the points from top view to front view including the points of intersection of cutting plane with the edges of pentagon (ie., the points 1, 2, 3 and 4). Locate the corresponding points in front view as 1', 2', 3', 4'. Hatch the surface. enclosed by the points 1', 2', 3', and 4'. which represent the sectional front view. To locate 3': With o as centre and o-3 as radius draw an arc to cut the o-c at 11. Draw the vertical projector through r1 to cut o'c' at r'1 and then draw horizontal projector through r'1 to cut o'b' at 3' Step 4 (True section): Draw another axis X1Y1, parallel to the cutting plane at any convenient distance and draw the projectors through the points 1, 2, 3 and 4, perpendicular to the XY line. Locate the points 1'1, 2'1, 3'1, and 4'1 on these projectors in such a way that there distances from X1Y1 are equal to the corresponding distances of points 1', 2', 3' and 4' from XY line. Join the points 1'1, 2'1, 3'1, and 4'1 in proper sequence and hatch the surface enclosed by the edges joined by these points which represents the true shape of the section as shown in fig. 15.29. Example 20: A Hexagonal pyramid, side of base 25 mm and axis 55 mm long, rests with its base on HP such that one of the edges of its base is perpendicular to VP. It is cut by a section plane perpendicular to HP, inclined at 45° to VP and passing through the pyramid at a distance of 10 mm from the axis. Draw the top view, sectional front view and the true shape of the section. The projections are shown above in fig. 15.30.1. Sections of Pyramids by a Horizontal Plane
2. Sections of Pyramids by a vertical plane
3. Sections of Pyramids by a plane inclined to HP and Perpendicular to VP
4. Sections of Pyramids by Planes inclined to VP and Perpendicular to HP
Engineering Graphics: Unit IV (a): Sections of Solids : Tag: : Construction, Steps, Example Problems | Engineering Graphics (EG) - Sections of pyramids
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
