Theory of Machines: Unit III: Friction in Machine Elements
screw jack
Friction in Machine Elements - Theory of Machines
The screw jack is a device used for lifting heavy loads by applying a comparatively smaller effort at its handle.
SCREW JACK • The screw jack is a device used for lifting heavy loads by applying a comparatively smaller effort at its handle. • The working principle of screw jack is similar to that of an inclined plane. A screw jack, with its spindle having square threads is shown in Fig.6.12(a). The load to be raised or lowered, is placed on the square threaded rod which is rotated by the application of an effort at the end of the tommy bar (lever). As we have already discussed that motion of nut on the screw is analogous to sliding along an inclined plane. Let W = Load to be lifted, P = Effort (i.e., horizontal force) applied at the screw tangentially, l = Horizontal distance between central axis of the screw and the end of the bar, μ = tan ϕ, coefficient of friction between the screw and nut, ϕ = Friction angle, α = Inclination of thread or helix angle, p = Pitch of the screw, and d = Mean diameter of the screw. If the nut is rotated so that the screw moves against the axial load W, then it is treated as body is moving upwards on the inclined plane as discussed in Section 6.7.1. All the forces acting on the screw are shown in Fig.6.12(b). Hence the equation (6.17) can be used as such. The turning moment or torque required to overcome friction between screw and nut is If the nut is rotated so that the screw moves along the axis load, then it is treated as body is moving downwards on the inclined plane, as discussed in Section 6.7.2. Hence equation (6.20) can be used as such. ⸫ Turning moment or torque required to overcome friction between screw and nut is given by When the axial load is taken up by a thrust collar as shown in Fig.6.13, then some torque is required to overcome friction at the collar also. The torque required to overcome collar friction is given by where μ1 = Coefficient of friction of the collar, R1 + R2 = Outside and inside radius of the collar, and R = Mean radius of the collar = R1 + R2 / 2 Now total torque required to overcome friction i.e., to rotate the screw is given by If effort P is applied tangentially at the end of a tommy bar/lever, then the total torque required to overconfe friction must be equal to torque due to force P applied at the end of the lever. • The efficiency of a screw jack may be defined as the ratio of ideal effort (ie., the tangential force required to move the load neglecting friction) to the actual effort (i.e., the tangential force required to move the load with friction). • As derived in Section 6.7.1, the efficiency of screw jack to raise load is given by and as derived in Section 6.7.2, the efficiency of screw jack to lower the load is given by • As derived in Section 6.7.3, the maximum efficiency of a screwjack for raising (or lowering) a load is given by We know that the effort required to lower the load in the screw jack, P = W tan (ϕ - α) and the torque required to lower the load, In the above expression, if ϕ < α, then the torque required to lower the load will be negative. In other words, the load will start moving downward without the application of any torque. Such a condition is known as overhauling of screw. This undesirable effect is removed by keeping the value of α always less than ϕ. On the other hand, if ϕ > α, then the torque required to lower the load will be positive, so an effort will be required to lower the load. This type of screw is termed as self-locking screw. Thus for a screw to be self-locking, friction angle must be greater than helix angle α. Note It may be noted that the efficiency of self-locking screws is less than 50%. If the efficiency is more than 50%, then screw is said to be overhauling. Example 6.6 A load of 10 kN is raised by means of a screw jack, having a square threaded screw of 12 mm pitch and of mean diameter 50 m. If a force of 100 N is applied at the end of a lever to raise the load, what should be the length of the lever used? Coefficient of friction = 0.15. What is the mechanical advantage obtained? State whether the screw is self locking or not. Given data: W = 10 kN = 10 × 103 N; p = 12 mm = 0.012 m; d = 50 mm = 0.05 m; P = 100 N; μ = tan ϕ = 0.15. Solution: Length of the lever used: We know that force required to raise the load of at the circumference of the screw, and torque required to overcome friction, Let P1 = Force required at the end of lever of length l. We also know that the torque, T = P1 × l Mechanical advantage: Check for self-locking: We know that, Since the efficiency of screw is less than 50%, therefore the screw is self-locking screw. Ans. Example 6.7 Pitch of 50 mm diameter threaded screw of a screw jack is 12.5 mm. Coefficient of friction between screw and nut is 0.10. Determine the torque to raise a load of 25 kN rotating with the screw. Also find the torque required to lower the load and efficiency of screw jack. Given data: d = 50 mm = 0.05 m; p = 12.5 mm = 0.0125 m; μ = 0.1; W=25 kN. Solution: We know that, Torque required to raise the load (T1): We know that torque required to raise the load, Torque required to lower the load (T2): We know that torque required to lower the load, Efficiency of screw jack (η): We know that, Example 6.8 A screw jack has a square thread of mean diameter 6 cm and pitch 0.8 cm. The coefficient of friction at the screw thread is 0.09. A load of 3 kN is to be lifted through 12 cm. Determine the torque required and the work done in lifting the load through 12 cm. Find the efficiency of the jack also. Given data: d = 6 cm = 0,06 m; p = 0.8 cm = 0.008 m; μ = 0.09; W = 3 kN = 3 ×103 N. Solution: (i) Torque required to raise the load: We know that the torque required to raise the load, (ii) Work done in lifting the load through 12 cm: In one complete revolution of the screwed rod, the load is lifted through a distance equal to pitch. Number of turns required to lift the load through a distance of 12 cm = 12 / 0.8 = 15 ⸫ Work done in lifting the load, W = 2π N T (iii) Efficiency of the screw jack: We know that, Example 6.9 The following data relate to a screw jack: Pitch of the threaded screw = 8 mm; Diameter of the threaded screw = 40 mm; Coefficient of friction between screw and nut = 0.1; Load = 20 kN. Assuming that the load rotates with the screw, determine: (i) the ratio of torques required to raise and lower the load, and (ii) the efficiency of the machine. Given data: p = 8 mm = 0.008 m; d = 40 mm = 0.04 m; μ = tan ϕ = 0.1; W = 20 kN = 20 × 103 N. Solution: (i) Ratio of torques required to raise and lower the load: (ii) Efficiency of the machine: We know that, Example 6.10 The efficiency of a screw jack is 55%, when a load of 1500 N is lifted by an effort applied at the end of a handle of length 0.5 m. Determine the effort applied if the pitch of the screw thread is 10 mm. Given data: η = 55%; W = 1500 N; l = 0.5 m; p = 10 mm = 0.01 m. Solution: We know that, We also know that the torque required to raise the load, We also know that the torque at the end of handle, Example 6.11 The mean diameter of the screw jack having pitch of 10 mm is 50 mm. A load of 20 kN is lifted through a distance of 170 mm. Find the work done in lifting the load and efficiency of the screw jack when (i) the load rotates with the screw, and (ii) the load rests on the loose head which does not rotate with the screw. The external and internal diameter of the bearing surface of the loose head are 60 mm and 10 mm respectively. The coefficient of friction for the screw as well as the bearing surface may be taken as 0.08. [A.U., Nov/Dec 2012]. Given data: p = 10 mm = 10 × 10-3 m; d = 50 × 10-3 m; W = 20 kN = 20 × 103 Ñ; D2 = 60 mm or R2 = 30 mm = 30 × 10-3 m; D1 = 10 mm or R1 = 5 mm 5 × 10-3 m; μ = tanϕ = μ1 = 0.08. Solution: Force required at the circumference of the screw to lift the load, Torque required to overcome friction at the screw, In one complete revolution of the screwed rod, the load is lifted through a distance equal to pitch. ⸫ Number of turns required to lift the load through a distance of 170 mm = 170/10 = 17 (i) When the load rotates with the screw: We know that the work done in lifting the load, and efficiency of the screw jack, (ii) When the load does not rotate with the screw: Mean radius of the bearing surface, Torque required to overcome the friction at the screw and the collar, ⸫ Work done by the torque in lifting the load, We know that the torque required to lift the load, neglecting friction,1. Screw Jack with Square Threads

2. Torque Required to Raise the Load W

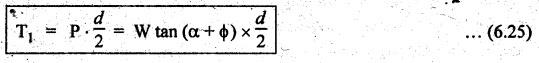
3. Torque Required to Lower the Load W

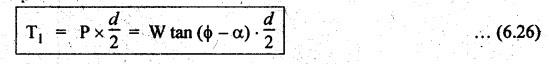
4. Torque Required to Overcome the Collar Friction
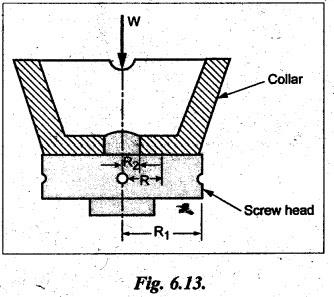

5. Total Torque Required


6. Efficiency of a Screw Jack




7. Overhauling and Self-locking Screws


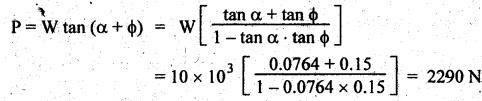


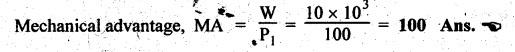
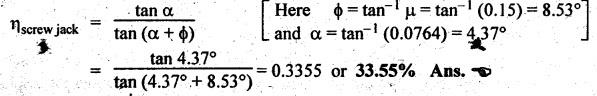
![]()
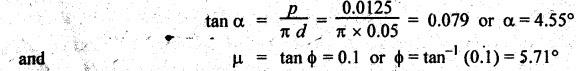
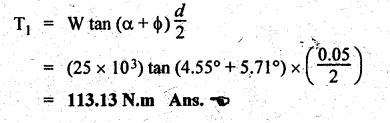


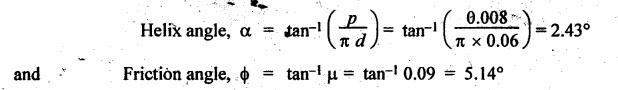







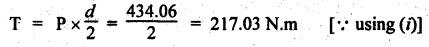
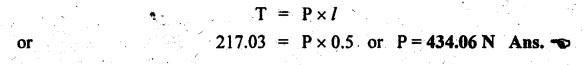
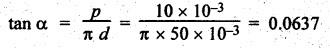




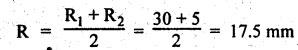
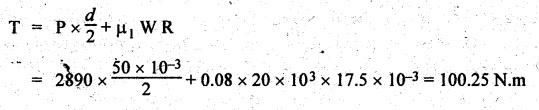

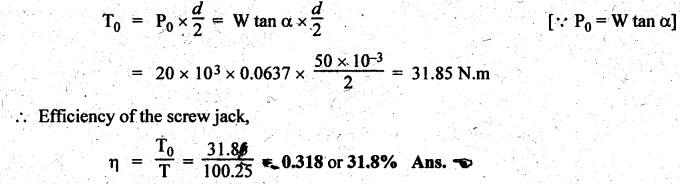
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - screw jack
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
