Engineering Physics: Unit IV: Basic Quantum Mechanics
Schrodinger Time Independent Wave Equation (Derivation)
Consider a wave associated with a moving particle.
SCHRODINGER TIME INDEPENDENT WAVE EQUATION (Derivation) Consider a wave associated with a moving particle. Let x, y, z be the coordinates of the particle and Ψ wave function for de - Broglie's waves at any given instant of time t. (Fig 6.6) The classical differential equation for wave motion is given by Here, v is wave velocity. The eqn (1) is written as The solution of eqn (2) gives Ψ as a periodic variations in terms of time t, Here, Ψ0 (x, y, z) is a function of x, y, z only which is the amplitude at the point considered. ω is angular velocity of the wave. Differentiating eqn (3) with respect to t, we get Again differentiating with respect to t, we have Substituting eqn (4) in eqn (2), we have We know that angular frequency Squaring eqn (6) on both sides, we get Substituting eqn (7) in eqn (5), we have If E is total energy of the particle, V is potential energy and 1/2 mv2 is kinetic energy, then Total energy = Potential energy + Kinetic energy Multiplying by m on both sides, we have Substituting eqn (10) in eqn (9), we get The eqn (11) is known as Schrodinger time independent wave equation for three dimensions. on substituting eqn (12) in eqn (13), Schrodinger time-independent wave equation is written as Note: In eqn (14), there is no term representing time. That is why it is called as time independent equation. If we consider one-dimensional motion ie., particle moving along only X - direction, then Schrodinger time independent equation (14) reduces to

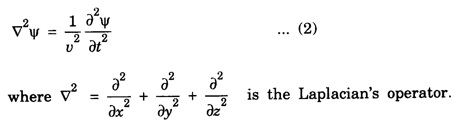
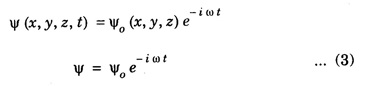
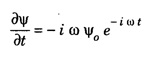
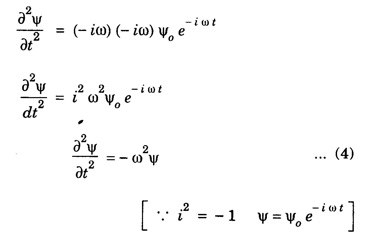
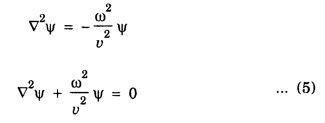
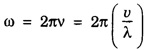

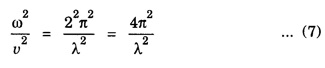

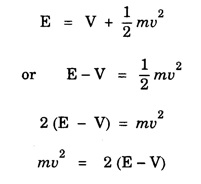




Special case

Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : - Schrodinger Time Independent Wave Equation (Derivation)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
