Engineering Physics: Unit I: Mechanics
Rotational Kinetic Energy and Moment of inertia
Consider a rigid body rotating about a fixed axis XOX ′. The rigid body consists of a large number of particles.
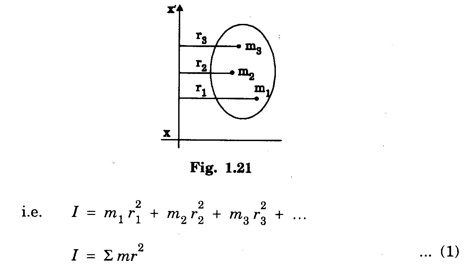
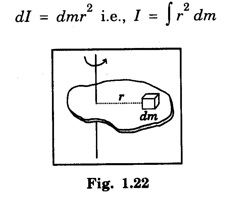
ROTATIONAL KINEMATICS Rotational Kinetic Energy and Moment of inertia Consider a rigid body rotating about a fixed axis XOX ′. The rigid body consists of a large number of particles. Let m1, m2, m3, ... etc. be the masses of the particles situated at distances r1, r2, r3,... etc. from the fixed axis. (Fig. 1.19) All the particles rotate with the same angular velocity W. But the linear velocities of the particles are different. and so on. Kinetic energy of the whole body is equal to the sum of the kinetic energy of all particles of the body ∴ Kinetic energy of the rigid body The term ∑ mr2 is called moment of inertia of a body about the given axis of rotation and denoted by I. i.e., I = ∑ mr2 ∴ The kinetic energy of the rigid body Moment of Inertia or Rotational inertia Inertia of a body is its inability to change by itself its state of rest or of uniform motion in a straight line. Similarly Moment of inertia of a body is its inability to change by itself its state of rest or of rotatory motion about an axis. An external force is necessary to change its state. • There is a tendancy to resist changes in uniform rotational motion. For example if a fan is switched off it continues to rotate for some more time before it comes to rest. • The property of a body by which it resists change uniform rotational motion is called rotational inertia or moment of inertia. The moment of inertia of a body depends on the mass of the body and also the distribution of the mass with respect to the axis of rotation. The moment of inertia of a particle about an axis is defined as the product of the mass of the particle and square of the distance of the particle from the axis of rotation. If 'm' is the mass of the particle and 'r' is the distance of the particle from the axis of rotation, (Fig 1.20) then The moment of inertia of the particle Consider a rigid body of mass M, rotating about an axis XX'. The body is supposed to be made of a large number of particles. If m1, m2, m3 are the masses of the particle and r1, r2, r3... their respective distances from the axis of rotation, then by definition, the moments of inertia of the particle about the axis of rotation are m1 r12, m2 r22, m3 r32... respectively. Then moment of inertia of the whole body is the sum of the moment of inertia of all the particles. The moment of inertia of a rigid body about a given axis is the sum of products of masses of its particles and the square of their respective distances from the axis of rotation. The unit of moment of inertia is kgm2. When angular velocity ω = 1 radian / sec It shows that moment of inertia of a body is equal to twice the kinetic energy of a rotating body when angular velocity is one radian per second. Note 1. Moment of inertia depends on mass, distribution of mass and on the position of axis of rotation. 2. Moment of inertia does not depend on angular velocity, angular acceleration, torque, angular momentum and rotational kinetic energy. 3. Moment of inertia of a continuous distribution of mass, treating the element of mass dm at position r as particle (Fig 1.22) 4. It is not a vector as direction (clockwise or anti-clockwise) is not to be specified and also not a scalar as it has different values in different directions. 5. In case of a hollow and solid body of same mass, radius and shape for a given axis, moment of inertia of hollow body is greater than that for the solid body because it depends upon the mass distribution. The property which opposes the change in rotational motion of the body is called the moment of inertia. Greater is moment of inertia of the body about the axis of rotation, greater is the torque required to rotate the body. Thus it is clear that the moment of inertia of a body has the same role in rotational motion as that of mass (or inertia) is linear motion. It is clear that the moment of inertia of a body depends on (i) mass of body and (ii) distribution of mass about the axis of rotation. The two bodies of same mass may have different moment of inertia 1. Fly-wheel A fly-wheel is such a heavy wheel whose most of the mass is concentrated at the rim, so that its moment of inertia is quite large. This wheel is attached to the shaft of the engine in which the torque rotating the shaft changes periodically. 2. Wheels of vehicles In cycle, riksha, car, motor car, scooter etc. the moment of inertia of wheels is increased by concentrating most of the mass at the rim of the wheel and connecting the rim to the axle of the wheel through the spokes. Due to large moment of inertia of wheels, they cause greater opposition to the change in their state of rotational motion. If the whole mass of the rigid body 'M’ is assumed to be concentrated at a distance of 'K' from the axis of rotation then Here M = Σ m K is known as radius of gyration. Definition The radius of gyration is defined as the distance from the axis of rotation to the point where the entire mass of the body is assumed to be concentrated. If the body consists of n particles of equal mass m, then the moment of inertia. put m1 = m2 = m3 = ... = mn = m and multiplying and dividing by n, we get where M = nm is the mass of the body and K is called the Radius of Gyration of the body about the axis of rotation. It is equal to the root mean square distance of all particles from the axis of rotation of the body. Hence the radius of gyration of a body about a given axis is equal to root mean square distance of the constituent particles of the body from the given axis. 1. Radius of gyration (K) depends on shape and size of the body, position and configuration of the axis of rotation, distribution of mass of the body w.r.t. the axis of rotation. 2. S.I. unit : Metre. 3. Significance of radius of gyration: Through this concept a real body (particularly irregular) is replaced by a point mass for dealing its rotational motion. Example: In case of disc rotating about an axis through its centre of mass and perpendicular to its plane So instead of disc we can assume a point mass M at a distance R/ √2 from the axis of rotation for dealing the rotational motion of the disc.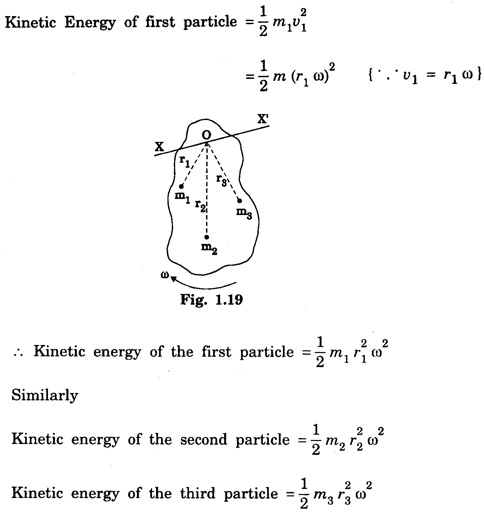
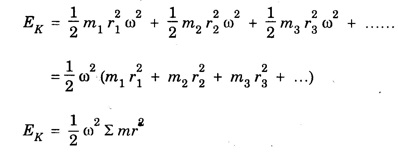
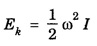
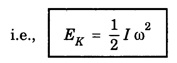
Moment of inertia of a particle
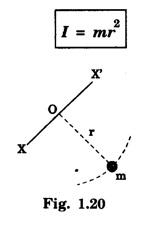 The unit of moment of inertia is kgm2
The unit of moment of inertia is kgm2Moment of inertia of a rigid body
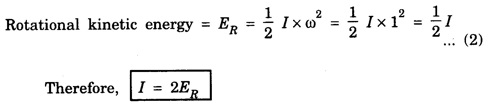
Physical significance of Moment of Inertia
Practical utility of Moment of Inertia
Radius of Gyration

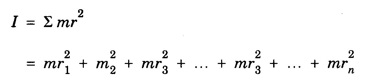
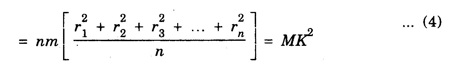
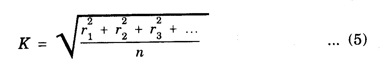
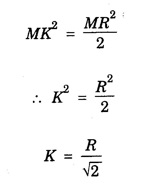
Engineering Physics: Unit I: Mechanics : Tag: : - Rotational Kinetic Energy and Moment of inertia
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
