Rotational Energy states of a rigid diatomic molecule

If we consider two atoms of masses m1 and m2 which are situated at a distance r1 and r2 with respect to the axis of rotation YY' respectively, then this arrangement is called as rigid rotor. Here 'R' is the bond length between the two atoms (R = r1 + r2).

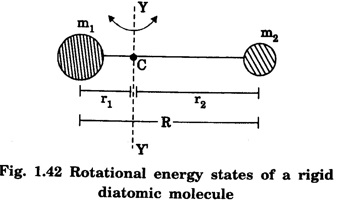
If the distance diatomic molecule rotates with respect to the center of mass 'C', then its kinetic energy is given as

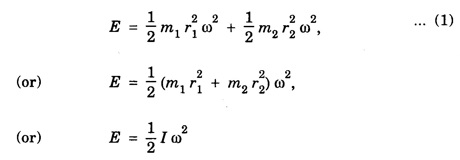
(because, the moment of inertia I = m1 r12 + m2 r22)

E = 1/2 I ω2,                        ... (2)

The eqn.(2) can be rewritten as,

E = 1/2 I . I 2ω2               …. (3)                        

As, I ω = L, (the angular momentum of the rigid rotor), then Eq.(3) becomes

At atomic level, the rotation leads to quantization of the angular momentum with values given by

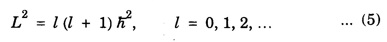
where 'l’ is the rotational quantum number. As 'l’ varies interms of integer values, so corresponding the energy levels of a rotating molecule are therefore given by

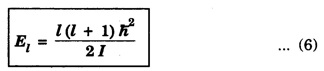
The ground level and first four excited rotational energy. levels for a diatomic molecule is shown in the fig. 1.43.

Note that the levels are not equally spaced.