Theory of Machines: Unit III: Friction in Machine Elements
Review and summary
Friction in Machine Elements - Theory of Machines
Based on the shape of cross-section of the belts, belts are classified as flat belts, V- belts and ropes (i.e., circular belts).
REVIEW AND SUMMARY • Based on the shape of cross-section of the belts, belts are classified as flat belts, V- belts and ropes (i.e., circular belts). • Velocity ratio of belt drive: where N1 and N2 = Speeds of the driver and driven pulleys respectively, d1 and d2 = Diameters of the driver and driven pulleys respectively, t = Thickness of the belt, s = Total percentage slip, E = Young's modulus of the belt material, and σ1 and σ2 = Stresses in the belt on tight and slack sides respectively. Velocity ratio of a compound belt drive: • Length of an open belt: • Length of the cross belt: where d1 and d2 = Diameters of the larger and smaller pulleys respectively, and x = Distance between the centres of two pulleys. • Determination of angle of contact: For open belt drive: For cross belt drive: • Tension ratio for flat belt drive: • Power transmitted by a belt; P = (T1 - T2) v where P = Power transmitted by a belt in watts, T1 and T2 = Tensions in the tight and slack sides of the belt in newtons respectively, and v = Linear velocity of the belt in m/s. • Centrifugal tension: TC = m v2 where m = Mass per unit length of belt • To find the width of the belt, use the formula, Tmax = σ • b • t where σ = Maximum safe stress, b = Width of belt, and t = Thickness of belt • Conditions for the transmission of maximum power are: • Initial tension (T0) of the belt: • Tension ratio for V-belts and rope drives: • Number of V-belts (or ropes) = 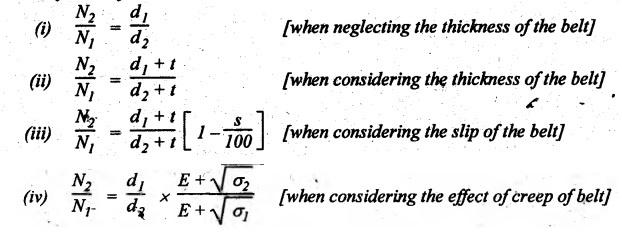
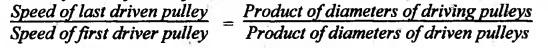
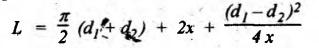
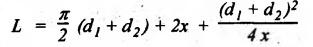

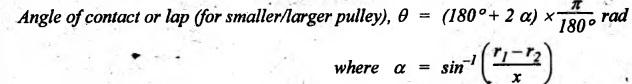
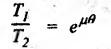
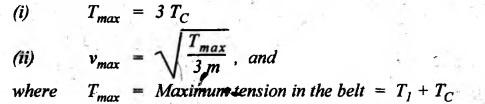
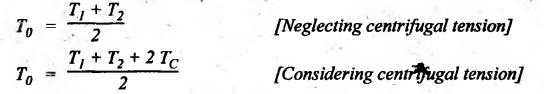
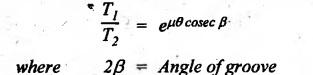
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - Review and summary
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
