Review and summary

REVIEW AND SUMMARY

• The determination of motion characteristics such as displacement, velocity and acceleration of various links for a given input motion is known as kinematic analysis.

• Important methods of determining the kinematic analysis are:

1. Graphical method:

(i) Relative velocity method, and

(ii) Instantaneous centre method.

2. Analytical or algebraic method

• All the abovesaid methods are discussed widely with sufficient example problems, in this chapter.

• Configuration diagram is a skeleton or a line diagram which represents a machine or a mechanism.

• Velocity of any point on a link with respect to another point on the same link is always perpendicular to the line joining these points on the configuration diagram. • Two components of acceleration are:

(i) Radial or centripetal component: It acts in the direction parallel to the link and its direction is towards the centre of rotation.

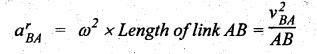
(ii) Tangential component: It acts in the direction perpendicular to the link.

a^t_BA = α × Length of link AB = α × AB

(iii) Total acceleration = Vector sum of radial and tangential accelerations

a_BA = a^r _BA + a^t _BA

• If a link rotates at a constant angular velocity, then the tangential component of acceleration at become zero.

• If a link (like slider) moves in a straight line, then the radial component of acceleration ar becomes zero.

• When a point on one link is sliding along another rotating link, then the point is known as coincident point.

• Whenever a coincident point exists in a mechanism, we have to consider Coriolis component of acceleration.

• Magnitude of Coriolis component of acceleration, a^c = 2 v^sω

• The combined motion of rotation and translation of link may be assumed to be a motion of pure motion about some centre I, known as instantaneous centre.

• Number of instantaneous centres in a mechanism (N) is given by, N = n(n – 1) / 2 where n = Number of links.

• Kennedy's theorem states that if three bodies move relatively to each other, they have instantaneous centres and lie on a straight line.

• The angular velocity ratio theorem states that the angular velocity ratio of two links relative to a third link is inversely proportional to the distances of their common instantaneous centre from the respective centres of rotation.

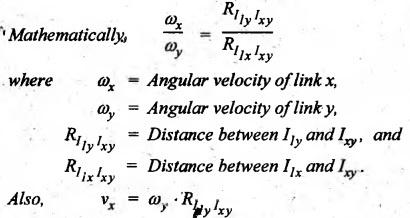
• Analytical method for velocity and acceleration of slider-crank mechanism: