Review and summary

REVIEW AND SUMMARY

• The study of mechanisms involves both their analysis as well as synthesis.

1. Analysis of mechanisms involves the study of motion and forces concerning different parts of the mechanism.

2. Synthesis of mechanisms involves the design of various parts of a machine concerning (1) its shape and size, (ii) materials to be used, and (iii) the arrangement of parts so that the resulting machine can perform the desired tasks.

• A kinematic link, also known as simply a link or an element, is defined as a single part (or an assembly of rigidly connected parts) of a machine which has motion relative to some other part of the machine.

• Types of links:

1. Rigid link

2. Flexible link

3. Fluid link

• Structure is an assemblage of number of resistant bodies having no relative motion between them.

• The three types of constrained motions in kinematic pairs are:

1. Completely constrained motion

2. Incompletely constrained motion

3. Successfully constrained motion

• When any two links are connected in such a way that the relative motion is completely or successfully constrained, they form a kinematic pair.

• Classification of kinematic pairs:

1. Depending upon the nature of relative motion between the links:

1. Sliding (or prismatic) pair

2. Turning (or revolute) pair

3. Screw (or helical) pair

4. Cylindrical pair

5. Spherical (or globular) pair

6. Rolling pair

II. Depending upon the nature of contact between the links:

1. Lower pair: If a kinematic pair in motion has a surface or area contact between the two links, it is called a lower pair.

2. Higher pair: If a kinematic pair in motion has a line or point contact between the two links, it is called a higher pair.

III. Depending upon the nature of mechanical arrangement between the links:

1. Closed (or self-closed) pair

2. Force closed (or unclosed or open) pair

• A kinematic chain is defined as the combination of kinematic pairs in which each link forms a part of two kinematic pairs and the relative motion between the links is either completely constrained or successfully constrained.

• The required equations/conditions to form a kinematic chain are:

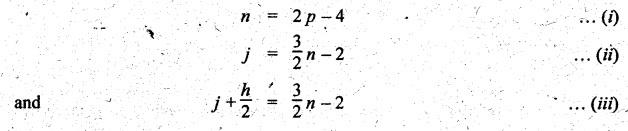
where

n = Number of links,

p = Number of pairs,

j = Number of binary joints, and

h = Number of higher pairs.

• A.W. Klien's criterion of constraint to determine the nature of chain:

In equation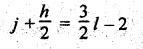 

(i) If L.H.S > R.H.S., then the given chain is called locked chain or structure.

(ii) If L.H.S. = R.H.S., then the given chain is called constrained kinematic chain.

(iii) If L.H.S. < R.H.S., then the given chain is called unconstrained kinematic chain.

• Types of joints in a chain:

1. Binary joint

2. Ternary joint: One ternary joint is equivalent to two binary joints.

3. Quaternary joint: One quaternary joint is equivalent to the three binary joints.

• Mechanism Vs. Machine:

■ A mechanism is a device to transmit and modify motion.

■ A machine is a mechanism or a collection of mechanisms which transmits both promotion and forces.

• The degree of freedom is the number of independent parameters required to specify the location of every link within a mechanism.

• The mobility of a mechanism is defined as the number of inputs required to produce the constrained motion of the mechanism.

• Grubler's equation for planar mechanism:

DOF = 3 (n - 1) — 2l - h

where DOF = Degrees of freedom of the mechanism,

n = Number of links,

l = Number of lower pairs (or binary joints), and

h = Number of higher pairs.

1. If DOF = 0, the device is a statically determinate structure.

2. If DOF ≥ 1, the device is a mechanism having constrained motion.

3. If DOF ≤ -1, the device is a statically indeterminate structure.

• Kutzbach equation for spatial mechanism:

DOF = 6 (n - 1) -5p₁ - 4p₂ -3 p₃ - 2 p₄ - 1 p₅

where n₁ = Number of links,

p₁ = Number of pairs having 1 DOF,

p₂ = Number of pairs having 2 DOF, and so on.

• The process of obtaining different mechanisms by fixing different links in a kinematic chain is known as kinematic inversion.

• Types of kinematic chain:

1. Four-bar chain

2. Single slider-crank chain

3. Double slider-crank chain

• Grashof's law states that for a planar four-bar mechanism, the sum of the shortest and gest links must be less than or equal to the sum of the lengths of other two links, if there is to be continuous relative motion between two members.

• Grashof's law: s + l ≤ p + q

where s and l = Lengths of the shortest and longest links respectively, and

p and q = Lengths of the other two links.

The four-bar chain that satisfies the Grashof's law is known as Grashof's chain.