Hydraulics and Pneumatics: Unit I: Fluid Power Priniciples and Hydraulic Pumps
Review and Summary
Fluid Power Priniciples and Hydraulic Pumps - Hydraulics and Pneumatics
In this chapter, the basics of hydraulics such as the concepts of force, pressure and head; concept and applications of Pascal's law;
REVIEW AND SUMMARY • In this chapter, the basics of hydraulics such as the concepts of force, pressure and head; concept and applications of Pascal's law; difference between laminar and turbulent flow; definition and significance of Reynolds number; and the concept and applications of Darcy's equation have been discussed, in detail. • Pressure head, P = ρ g h • If the pressure is measured with reference to the atmospheric pressure, then it is called gauge pressure. Any pressure measured above the absolute zero pressure is termed as 'absolute pressure'. Absolute pressure = Gauge pressure + Atmospheric pressure Vacuum pressure = Atmospheric pressure - Absolute pressure • Work = Force × Distance moved • Power = Work done/Time taken • Energy is capacity to do work. • Torque = Force × Moment arm = F × R • Power transmitted by a shaft, P = 2πΝΤ / 60 • Efficiency, η = Input power/ Output power • Pascal's law: The pressure applied to a confined fluid is transmitted undiminished in all directions. • The two important applications of Pascal's law are: 1. Bramah's hydraulic press, and 2. Air-to-hydraulic pressure booster. • In a hydraulic press, the output force is greater than the input force, but the output movement will be lesser than the input movement. • Reynolds number: Re = ρVD / μ = VD / v where the notations have usual meanings. • If Re < 2000, then the flow is laminar. If Re > 4000, then the flow is turbulent. If 2000 < Re < 4000, then the flow is unpredictable. • Flow rate or discharge: • Continuity equation : Q = A1 V1 = A2 V2 = Q2 • Total energy (or head) of a liquid in motion, • Bernoulli's equation: • Energy equation (Modified Bernoulli's equation) : • Darcy's equation is used to calculate the head loss due friction in the pipes. • Laminar friction factor: f = 64/Re • Hagen-Poiseuille equation: • Relative roughness = ε / Ꭰ • Head loss in valves and fittings: • At the end of the chapter, some illustrative examples are presented for better understanding of the basics. Pascal's law Hydraulic press Hydraulic jack Air-to-hydraulic pressure booster Force Pressure head Pressure Atmospheric pressure Gauge pressure Absolute pressure Flow rate Vacuum pressure Discharge Work Power Energy Torque Efficiency Laminar flow Turbulent flow Reynolds number Continuity equation Fluid energy in motion Bernoulli's equation Energy equation Modified Bernoulli's equation Energy losses in pipes Darcy's equation Friction factor Hagen-Poiseuille equation Relative roughness Moody diagram K-factor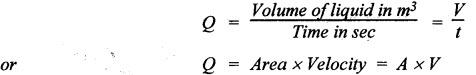
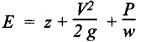
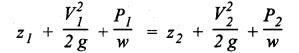
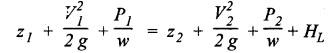
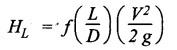
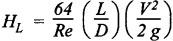
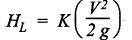
KEY TERMS ONE SHOULD REMEMBER
Hydraulics and Pneumatics: Unit I: Fluid Power Priniciples and Hydraulic Pumps : Tag: : Fluid Power Priniciples and Hydraulic Pumps - Hydraulics and Pneumatics - Review and Summary
Related Topics
Related Subjects
Hydraulics and Pneumatics
ME3492 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
