Theory of Machines: Unit II: Gears and Gear Trains
Reverted gear train
Gears and Gear Trains - Theory of Machines
The compound gear trains Can be subdivided into two types:
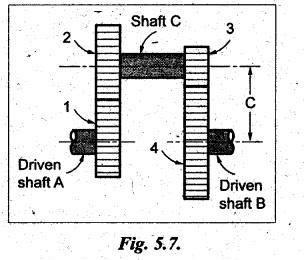
REVERTED GEAR TRAIN • The compound gear trains Can be subdivided into two types: 1. Reverted gear train, and 2. Non-reverted gear train. • A compound gear train in which the first and last gears are co-axial is called as reverted gear train. • Co-axial means the coincidence of axis of the two shafts. • Any compound gear train in which the first and last gears are not co-axial is called non-reverted gear train. • Applications: The reverted gear trains are used in: • Automotive gear boxes • Lathe back gears (to provide slow spindle speed) • Clocks (to connect hour hand and minute hand that are co-axial) • Fig.5.6 shows a reverted gear train. In this, input gear 1 and output gear 4 are co-axial. • Train value: Train value of reverted gear train is the same as that for the compound gear train (i.e., equation (5.4)). where N1, N2, N3 and N4 = Speed of gears 1, 2, 3, and 4 respectively, and T1, T2, T3 and T4 = Number of teeth of the gears 1, 2, 3, and 4 respectively. • From the Fig.5.6, it is agreed that the distance between the centres of the shafts of gears 1 and 2 and gears 3 and 4 are the same. If r1, r2, r3 and r4 are the pitch circle radii of gears 1, 2, 3 and 4 respectively, then • Assuming common module for all the four gears, we can write Now from equation (5.5(b)), we can write Equations 5.5(a), (b) and (c) can be used to determine the number of teeth on each gear of the reverted gear train. Note It should be borne in mind that the mating gears must have same module or circular pitch. Example 5.4 In a reverted gear train, as shown in Fig.5.7, two shafts A and B are in the same straight line and are geared through an intermediate parallel shaft C. The gears connecting A and C have a module of 2 and those connecting C and B have a module of 3.5. Speed of B is less than 1/10 that of A. If two pinions have each 24 teeth, find suitable teeth for the gears, and corresponding distance of shaft C from A. Given data: Solution: Refer Fig.5.7. 1. Suitable teeth for the gears: Let r1, r2, r3 and r4 = Pitch cfrele radius of gears 1, 2, 3 and 4 respectively, d1, d2, d3 and d4 = Pitch circle diameter of gears 1, 2, 3 and 4 respectively, T1, T2, T3 and T4 = Number of teeth on gears 1, 2, 3 and 4 respectively, m1, m2, m3, and m4 = Module of teeth on gears 1, 2, 3 and 4 respectively, and NA and NB = Speed of shafts A and B respectively. Given: We know that for reverted gear train, Substituting the value of T2, we get (18 + 1.7574) T4 = 6336 2. Distance between shaft C and A: We know that the centre distance,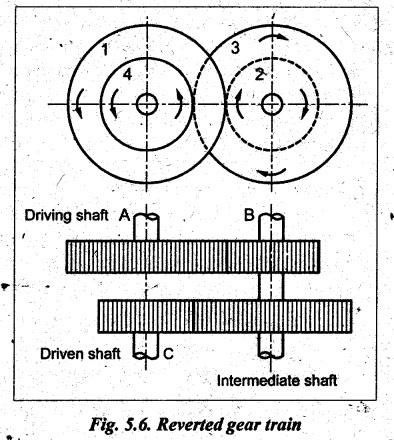
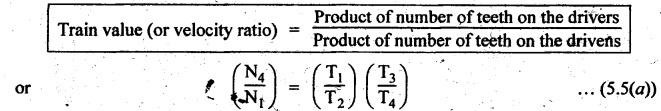

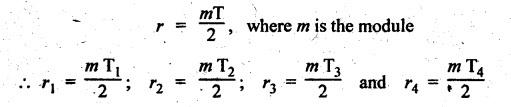
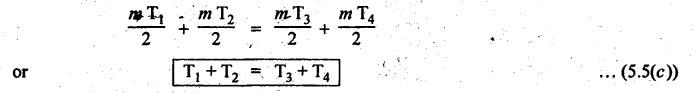
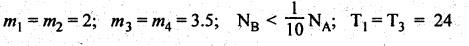
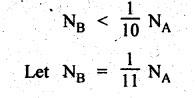
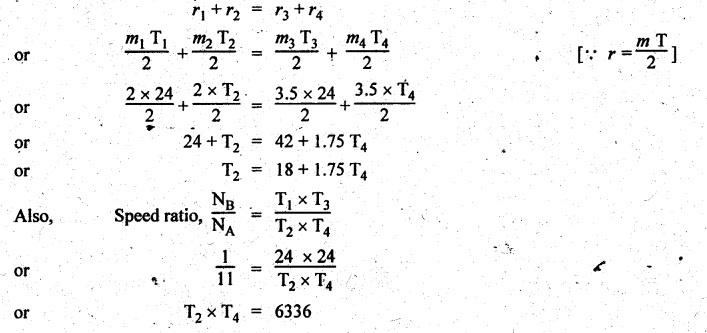
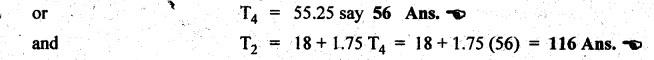
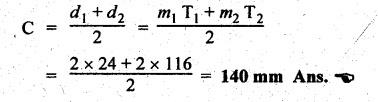
Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - Reverted gear train
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
