Engineering Physics: Unit III: a. Oscillations
Resonance
Theory of resonant vibrations, Examples, Simple experiment on Resonance
It is a special case of forced vibration The phenomenon of making a body vibrate with its natural frequency under the influence of another vibrating body with the same frequency is called resonance.
RESONANCE It is a special case of forced vibration The phenomenon of making a body vibrate with its natural frequency under the influence of another vibrating body with the same frequency is called resonance. If the frequency of the external periodic force is equal to the natural frequency of oscillation of the system, we get oscillations of larger amplitude. This is known as resonance. Amplitude becomes larger if the two frequencies are exactly equal to each other. v = vʹ (Fig 3.8) (a) Condition of amplitude resonance: In case of forced vibrations, we have The expression (1) shows that the amplitude varies with the frequency of the force p. For a particular value of p, the amplitude becomes maximum. This phenomenon is known as amplitude resonance. The amplitude is maximum when Thus the amplitude is maximum when the frequency This frequency of the system both in presence of damping, ρ = ω Using equation (1), A is maximum only when, For negligible damping, b = 0 and The rate of change (fall) of amplitude with the change of forcing frequency on each side of resonant frequency is known as sharpness of resonance. Figure 3.9 shows the variation of A with forcing frequency at different conditions of damping. The curve (1) shows the amplitude when there is no damping, i.e., b = 0. In this case the amplitude becomes infinite at p = ω. This case is never attained in practice due to frictional resistance, as slight damping is always present. The curve (2) and (3) shows the effect of damping on the amplitude. It is observed that the peak of the curve moves towards the left. (i) Two tuning forks of same frequency are mounted on a suitable sound boards and arranged as shown in fig.3.10. If one is made to vibrate by striking it with rubber hammer, it is found that the second fork is also set in vibrations. If the vibrations of the first fork is stopped by touching with hand. The second fork continue to vibrate and the sound will be heard. (ii) A column of army marching over a bridge can set forced vibrations of the bridge. If the frequency of foot steps matches with natural frequency of the bridge, due to resonance, the bridge may vibrate with a larger amplitude. This may cause damage to the bridge. Hence soldiers are asked to break steps while crossing a bridge. Radio stations have their own broadcasting (carrier) frequencies. When we tune our radio set, the moment the radio tuner attains exactly the frequency of any broadcasting station, we start hearing the loud and clear sound of that particular radio station due to resonance. The loud speaker diaphragm vibrates according to the amplifier circuit. Air column in resonance tube vibrates as per the vibrations of the tuning fork. From an elastic chord a number of pendulums are suspended (Fig. 3.11). If the pendulum P is set into vibrations, other pendulums also vibrate because they are attached to the same chord. But their motions are not regular. After sometime we will notice that Q which is the same length as P, vibrate with maximum amplitude and of same time period. They are said to be in resonance. Other pedulums of different lengths are not in resonance.
Theory of resonant vibrations


![]() of the impressed force becomes
of the impressed force becomes  This is known as the resonant frequency.
This is known as the resonant frequency.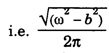 and in the absence of damping i.e.
and in the absence of damping i.e. 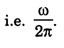
Condition for Amplitude Resonance
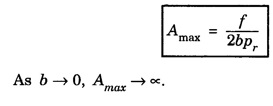
Sharpness of Resonance
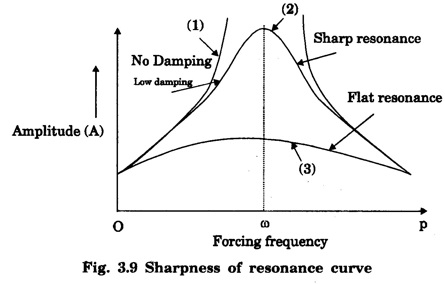
Examples

(iii) Radio receivers
(iv) Other Examples
Simple experiment on Resonance

Engineering Physics: Unit III: a. Oscillations : Tag: : Theory of resonant vibrations, Examples, Simple experiment on Resonance - Resonance
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
