Engineering Mechanics: Unit V: Dynamics of Particles
Rectangular Components
with Solved Example Problems | Curvilinear Motion
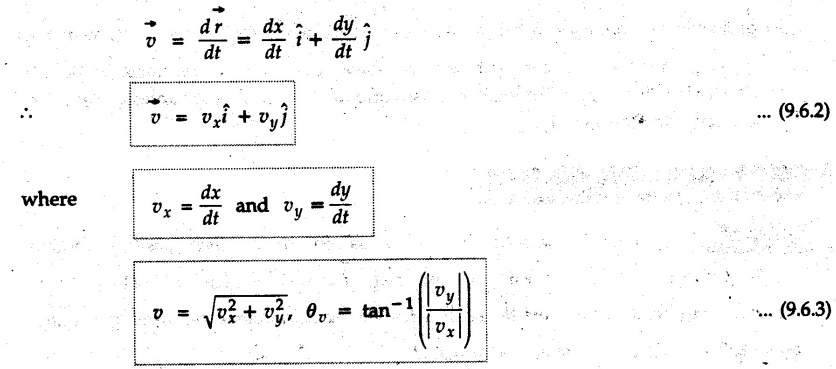
The position vector r of a particle in rectangular components written as
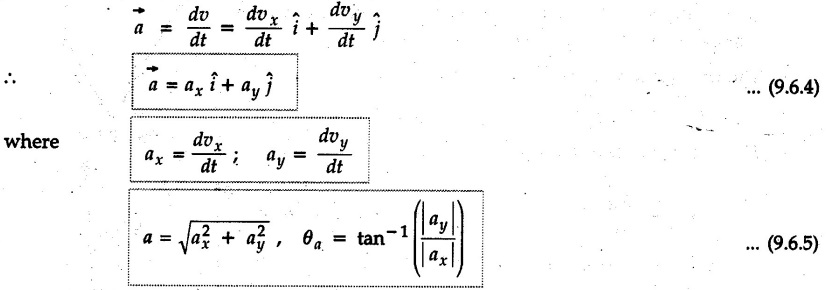
Rectangular Components • The position vector where x and y are functions of 't'. Differentiating w.r.t. 't', we get • Differentiating again w.r.t. 't', • The procedure for analysis of problems depends on the available data. These are summarized as follows, i) If acceleration is variable in any direction (x or y), use basic definitions and either differentiate or integrate the functions. ii) If acceleration is constant in any direction, use kinematical equations in that direction. iii) To obtain equation of path, get x any y in terms of a parameter like 't’ or any angle ‘θ’. Then eliminate the parameter to obtain equation relating x and y which is equation of path. iv) If an equation relating x and y is given and x, vx, ax are given, differentiate the given equation to get dy/dt (i.e. vy) in terms of dx/dt (i.e. vx). Again differentiate to get ay. v) In projectile motion, ax = 0 and ay = − g = −9.81 m/s2. As the acceleration in x as well as y direction is constant, we can use kinematical equations in X and Y-directions. This type of motion is most common in curvilinear motion. Hence we will discuss this separately. Example 9.6.1 The motion of particles A and B is defined by their position vectors Solution: The two particles collide when Time is not negative and the common solution for the two equations is t= 2 seconds. ⸫ The point where they collide is (10, 25). Example 9.6.2 A particle moves along the path y = 4x2 + 8x + 10 starting with an initial velocity Solution: Given Again differentiate w.r.t. 't' Substituting the values in equation (1) and (2), Example 9.6.3 The Y-co-ordinate of a particle maving along a curve is y = t3 - 61 + 3 where y is in metres and t in seconds. Its acceleration in x-direction is given by ax = 4t +3 m/s2. If velocity of the particle in x direction is 2 m/s when t = 0, calculate the magnitude and direction of velocity and acceleration of the particle when t = 1s. Solution : Example 9.6.4 The velocity of a particle moving in x-y plane is given by Solution : Angle between average acceleration vector and velocity vector at t = 4 s = 63.43 - 21.8 = 41.63°.![]() of a particle in rectangular components written as
of a particle in rectangular components written as
Solved Examples for Understanding
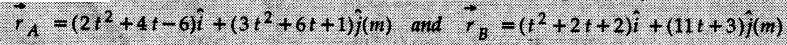 where t is in seconds. Determine the point where the particles collide and their speeds just before collision. At what time do they collide ?
where t is in seconds. Determine the point where the particles collide and their speeds just before collision. At what time do they collide ?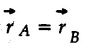

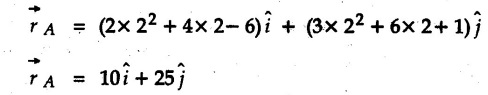
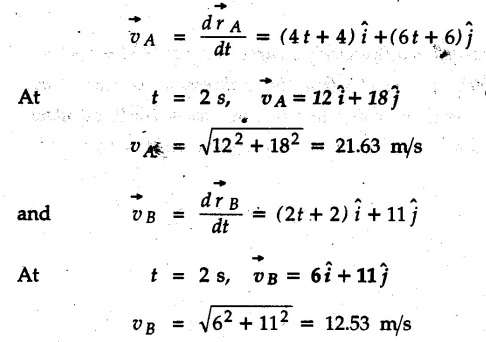
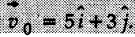 If vx is constant, determine vy, and ay at x = 3 m.
If vx is constant, determine vy, and ay at x = 3 m.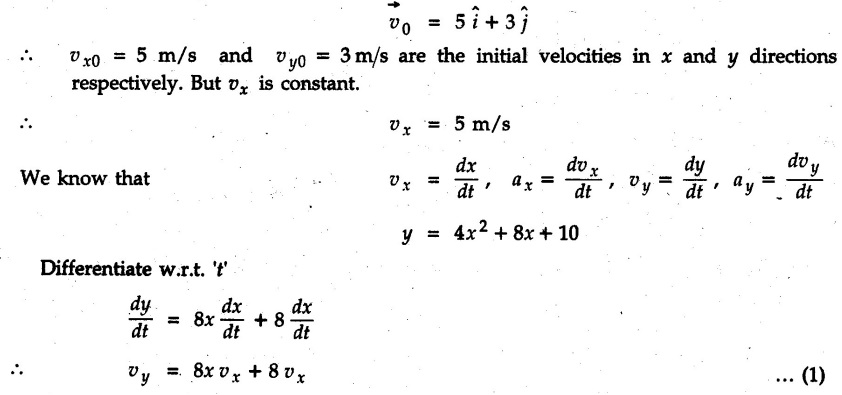

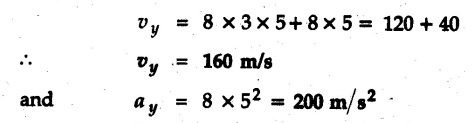

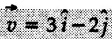 m/s at t = 2 s. Its average acceleration during the next
m/s at t = 2 s. Its average acceleration during the next 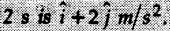 Determine the velocity at t = 4 s and the angle between the average acceleration vector and the velocity vector at t = 4s?
Determine the velocity at t = 4 s and the angle between the average acceleration vector and the velocity vector at t = 4s?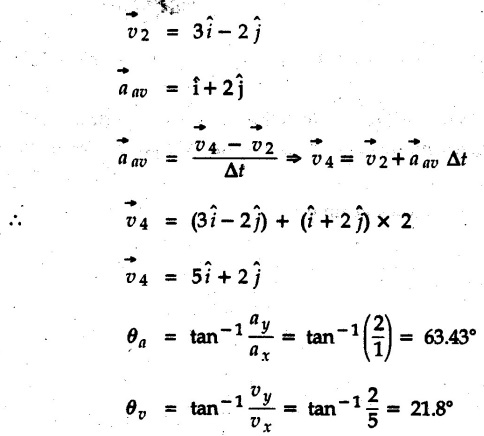
Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems | Curvilinear Motion - Rectangular Components
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
