Matrices and Calculus: Unit I: Matrices
Real Quadratic Form Reduction to Canonical Form
Matrices
A homogeneous polynomial of second degree in any number of variables is called a quadratic form.
REAL QUADRATIC FORM. REDUCTION TO CANONICAL FORM Definition 1.5.1 A homogeneous polynomial of second degree in any number of variables is called a quadratic form. For example (i) x2 + 4xy + 4y2 (ii) ax2 + by2 + cz2 + 2hxy + 2gyz +2 fzx (iii) x12 + x22 + 3x32 + x42 are quadratic forms in 2, 3 and 4 variables respectively. Definition 1.5.2 The general quadratic form in n variables x1, x2, …, xn, is A is a symmetric matrix and the quadratic form A is called the matrix of the quadratic form. For example the quadratic form x2 + 4xy + 4y2 can be written in the matrix Note Since the quadratic form Q = XT AX, it is obvious that the characteristics or properties of Q depend on the characteristics of A. Definition 1.5.3 A quadratic form Q which contains only the square terms of the variables is said to be in canonical form. For example x2 + y2, x2 − y2, x2 + y2 - 4z2 and x12 + x22 + 2x32 + x42 are in canonical forms because they contain only square terms. Let Q = XT AX be a quadratic form in n variables x1, x2, ..., xn and A = [aij] be the symmetric matrix of order n of the quadratic form. We will reduce A to diagonal form by an orthogonal transformation X = NY, where N is the normalised modal matrix of A. Then NT AN = D, where D is the diagonal matrix containing the eigen values of A. If λ1, λ2,..., λn are the eigen values of A, then This is the required quadratic form. Note In the canonical form the coefficients are the eigen values of A. Since A is a symmetric matrix, the eigen values of A are all real. So, the eigen values may be positive, negative or zero. Hence the terms of the canonical form may be positive, negative or zero. By using the canonical form or the eigen values we can characterise the quadratic form. Definition 1.5.4 If A is the matrix of the quadratic form Q in the variables x1, x2, ..., xn, then the rank of Q is equal to the rank of A. If rank of A < n, where n is the number of variables or order of A, then |A| = 0 and Q is called a singular form. Definition 1.5.5 Let Q = XT AX be a quadratic form in n variables x1, x2, ..., xn. X = [x1, x2, ..., xn]T and A is the matrix of the quadratic form. (i) Index of the quadratic form is the number of positive eigen values of A. (ii) Signature of the quadratic form is the difference between the number of positive and negative eigen values of A. (iii) Rank of the quadratic form is the number of positive and negative eigen values of A. Usually index is denoted by p, signature by s and rank by r. Definition 1.5.6 Let Q = XT AX be a quadratic form in n variables x1, x2, ..., xn. i.e., X = [x1 ... xn]T and A is the matrix of the quadratic form. (i) Q is said to be positive definite if all the n eigen values of A are positive. i.e., if r = n and p = n e.g., y12 + y22 +···+ yn2 is positive definite. (ii) Q is said to be negative definite if all the n eigen values of A are negative. i.e., if r = n, p = 0 e.g., -y12 - y22 -···- yn2 is negative definite. (iii) Q is said to be positive semidefinite if all the n eigen values of A are ≥ 0 with at least one eigen value = 0. i.e., if r < n and p = r e.g., y12 + y22 +···+ yr2, where r < n, is positive semi-definite. (iv) Q is said to be negative semidefinite if all the n eigen values of A are ≤ 0 with at least one value = 0. i.e., if r < n and p= 0 e.g., -y12 - y22 -···- yr2, where r < n, is negative semi definite. (v) Q is said to be indefinite if A has positive and negative eigen values. e.g., y12 + y22 - y32 – y42 +···+ yn2 is indefinite. (vi) We can also find the nature of a quadratic form without finding the eigen values of A or without reducing to canonical form but by using the principal minors of A as below. Definition 1.5.7 Let Q = XT AX be a quadratic form in n variables x1, x2, ..., xn and let the matrix of the quadratic form The determinants D1, D2, …., Dn are called the principal minors of A. The quadratic form Q is said to be (i) positive definite if Di > 0 for all i = 1, 2, ..., n (ii) negative definite if (-1)i Di > 0 for all i = 1, 2, ..., n i.e., D1, D3, D5, ... are negative and D2, D4, D6 ... are positive. (iii) positive semi-definite if Di ≥ 0 for all i = 1, 2, 3, ..., n and at least one Di = 0. (iv) negative semi-definite if (-1)i D ≥ 0 for all i = 1, 2, 3, ..., n and at least one Di = 0. (v) indefinite in all other cases. In the reduction of a quadratic form to canonical form the number of positive and negative terms are independent of the choice of the transformation. In other words, the signature of a real quadratic form is invariant under a real non-singular transformation. This property is called the law of inertia of the quadratic form. where aij are real numbers such that aij = aij for all i, j = 1, 2, 3, ....., n. Usually the quadratic form is denoted by Q and so Q =
where aij are real numbers such that aij = aij for all i, j = 1, 2, 3, ....., n. Usually the quadratic form is denoted by Q and so Q = 
1. Matrix form of Q

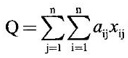 can be written as Q = XT AX.
can be written as Q = XT AX.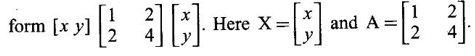
2. Canonical form of Q
3. Reduction of Q to canonical form by orthogonal transformation

4. Index, signature and rank of quadratic form
5. Definite and indefinite quadratic forms

7. Law of intertia of a quadratic form
Matrices and Calculus: Unit I: Matrices : Tag: : Matrices - Real Quadratic Form Reduction to Canonical Form
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
