Engineering Mechanics: Unit V: Dynamics of Particles
Radial and Transverse Components (Polar Co-ordinates)
with Solved Example Problems | Curvilinear Motion
When position of a particle is defined by the polar co-ordinates r and θ, the velocity and acceleration can be resolved into components known as radial and transverse components.
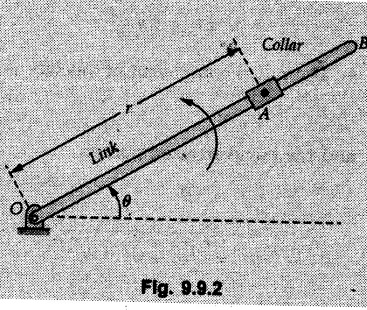
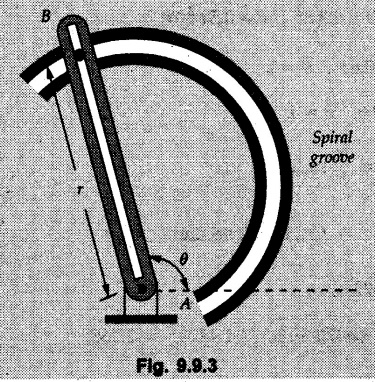
Radial and Transverse Components (Polar Co-ordinates) • When position of a particle is defined by the polar co-ordinates r and θ, the velocity and acceleration can be resolved into components known as radial and transverse components. • Let r and θ be the polar co-ordinates of a point P as shown in Fig. 9.9.1. • The co-ordinate r is the distance of point P from the origin and θ is the angle made by r with positive x-direction measured in anticlockwise sense. Let êr = Radial unit vector directed from O to P, i.e. radially outwards As êr and êθ have magnitude 1, The radial component of acceleration is and the transverse component • If 'r' and 'θ' are given as functions of 't' then differentiate them twice w.r.t. 't' to obtain Example 9.9.1 Link OB rotates about hinge O in vertical plane in anticlockwise direction starting from horizontal position. A collar can slide on the link as shown in Fig. 9.9.2. Angular position of link is given by θ = 0.5t2 and position of collar from hinge is given by r = 2t - 0.3t2, with the terms having usual meaning and S.I. units. Compute magnitude of velocity and acceleration of collar when θ = 60°. Solution: Example 9.9.2 The slotted arm AB drives the pin through the spiral groove described by the equation r=0.2eθ where r is in meters and θ in radians. If θ = 3 rad/s and is constant, determine the transverse compoment of the pin's acceleration when θ = 120°. Refer Fig. 9.9.3. Solution : Example 9.9.3 A circle of radius 'b' rolls over other fixed circle at some radius without slipping. A point on the circumference of rolling circle describes a cardioid defined by equations Solution: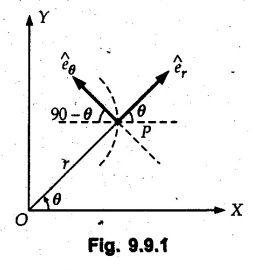




 Then use equations (9.9.5) to (9.9.14). If equation relating r and θ is given, differentiate w.r.t. 't' to get
Then use equations (9.9.5) to (9.9.14). If equation relating r and θ is given, differentiate w.r.t. 't' to get  in terms of
in terms of 
Solved Examples for Understanding
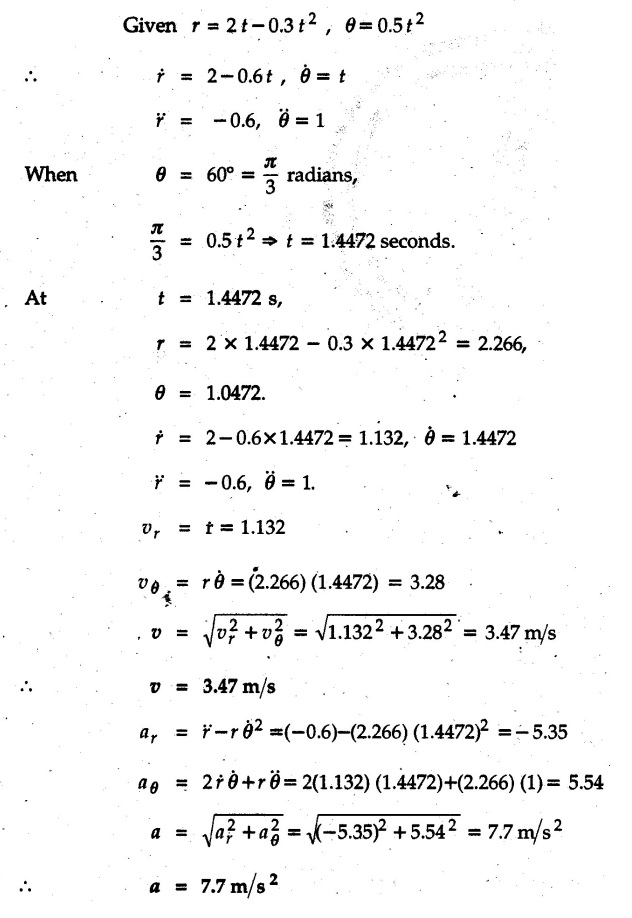

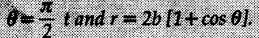 Obtain radial and transverse components of velocity and acceleration of the point when t = 1 s.
Obtain radial and transverse components of velocity and acceleration of the point when t = 1 s.
Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems | Curvilinear Motion - Radial and Transverse Components (Polar Co-ordinates)
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
