Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations
Questions and Answers
Applications of Partial Differential Equations | Transforms and Partial Differential Equations
Questions and Answers: Applications of Partial Differential Equations - Transforms and Partial Differential Equations
PART-A QUESTIONS AND ANSWERS 1. What conditions are assumed in deriving the one dimensional wave equation? See Page No. 3.13 2. What are the various solutions of See Page No. 3.11 3. A string is stretched and fastened to two points l apart. Motion is started by displacing the string into the form Solution: The displacement function y (x, t) is the solution of the wave equation. The boundary and initial conditions are 4. A string of length 2 l stretched to a constant tension T, is fastened at both the ends and hence fixed. The mid point of the string is taken to a height b and then released from rest in that position. It is desired to It solve for transverse vibrations of the string. Write the governing equation and the corresponding conditions. See Page No. 3.24 5. What is the constant a2 in the wave equation utt = a2 uxx? (OR) In the wave equation Solution : 6. State the suitable solution of the one dimensional heat equation Solution: 7. State the governing equation for one dimensional heat equation and necessary conditions to solve the problem. Solution: The one dimensional heat equation is where u (x, t) is the temperature at time t at a point distant x from the left end of the rod. The boundary conditions are (i) u (0,t) = k1°C for all t ≥ 0 (ii) u (l,t) = k2°C for all t ≥ 0 (l being the length of the one dimensional rod) The initial condition is (iii) u (x, 0) = f(x), 0 < x < 1 8. Write all variable separable solutions of the one dimensional heat equation u1 = α2 uxx Solution : 9. Write down the diffusion problem in one-dimension as a boundary value problem in two different forms. Solution : 10. State any two laws which are assumed to derive one dimensional heat equation. Sólution : (i) Heat flows from higher to lower temperature. (ii) The rate at which heat flows across any area is proportional to the area and to the temperature gradient normal to the curve. This constant of proportionality is known as the thermal conductivity (k) of the material. It is known as Fourier law of heat conduction. 11. Write any two solutions of the Laplace equation Uxx + Uyy = 0 involving exponential terms in x or y. Sol. 12. In steady state conditions, derive the solution of one dimensional heat flow equation. Solution: The p.d.e. of unsteady one dimensional heat flow is In steady state condition, the temperature u depends only on x and not on time t The general solution is u = ax + b where a, b are arbitrary. 13. Write the boundary conditions and initial conditions for solving the vibration of string equation, if the string is subjected to initial displacement f(x) and initial velocity g(x). Solution: The wave equation is 14. Write down the governing equation of two dimensional steady state heat conduction. Solution: The required equation is 15. The ends A and B of a rod of length 10 cm have their temperature kept at 20°C and 70°C. Find the steady state temperature distribution on the rod. Solution: 16. Write down the three possible solutions of Laplace equation in two-dimensions. Solution : Laplace equation in two-dimensions is V2 u = 17. Write down the partial differential equation governing the transverse vibrations of an elastic string. Solution : 18. Explain the various variables dominating the wave equation. Solution: The wave equation is y → displacement x → distance of the point on the string from fixed point along x direction t → time 19. Classify the partial differential equation Solution : 20. Classify the partial differential equation Solution : ⸫ the given equation is hyperbolic equation. 21. Classify the partial differential equation uxx + 2uxy + uyy = 0 Solution : 22. Classify the partial differential equation fxx + 2fxy + 4fyy = 0 Solution : Given fxx + 2fxy + 4fyy = 0 23. Classify the partial differential equation uxx + uxy + uyy = 0 Solution : ⸫ The given equation is an elliptic equation.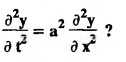
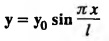 from which it is released at time t = 0. Formulate this problem as the boundary value problem.
from which it is released at time t = 0. Formulate this problem as the boundary value problem.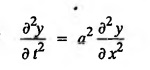
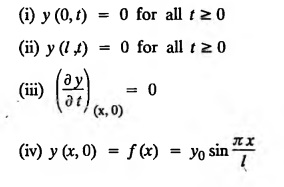
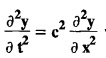 what does c2 stand for?
what does c2 stand for?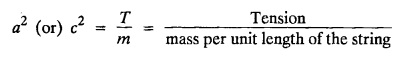
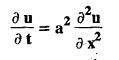
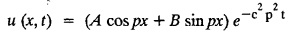
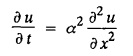
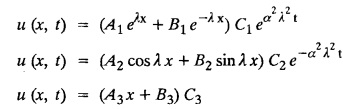
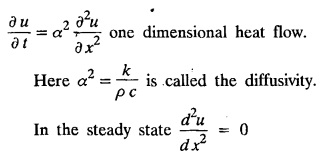
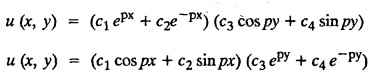
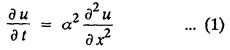
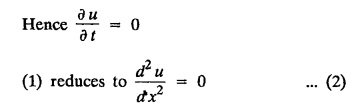
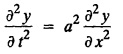
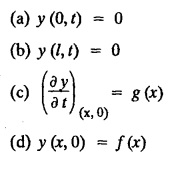
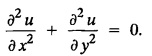

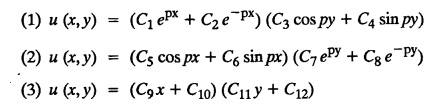
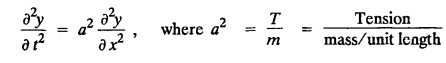
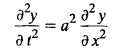
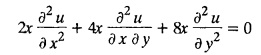

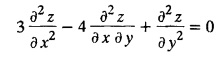
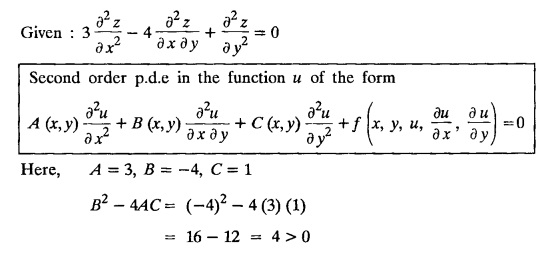
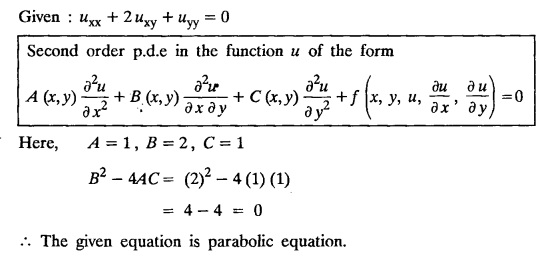

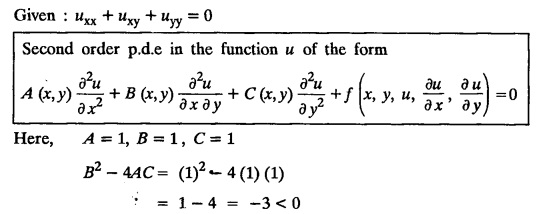
Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations : Tag: : Applications of Partial Differential Equations | Transforms and Partial Differential Equations - Questions and Answers
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
