Transforms and Partial Differential Equations: Unit II: Fourier Series
Questions and Answers
Fourier Series | Transforms and Partial Differential Equations
Questions and Answers - Part A - Fourier Series - Transforms and Partial Differential Equations
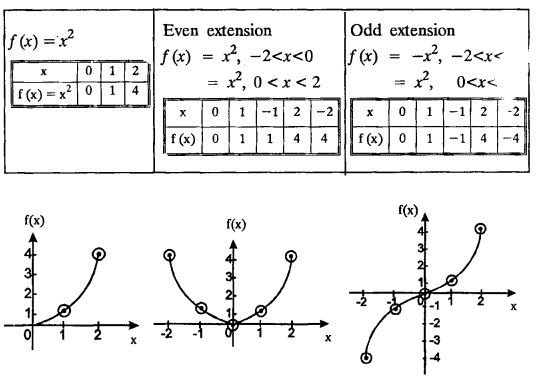
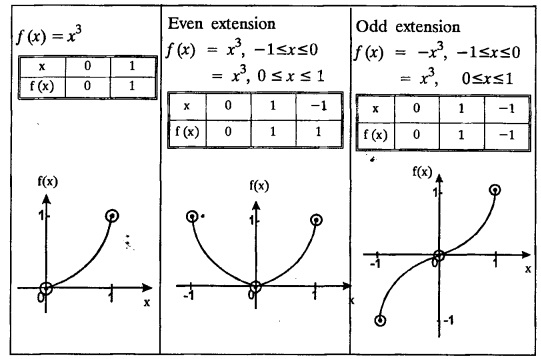
PART-A QUESTIONS AND ANSWERS I. Problems under (0, 2), (0, 2), (-л, л), (−l, l) 1. When does a function possess a Fourier series expansion in terms of trignometric terms? (or) State the conditions for f(x) to have Fourier series expansion. (or) Explain Dirichlet's conditions. Solution : See Page No. 2.13 2. State whether y = tan x can be expanded as a Fourier series. If so how? If not why? Solution: tanx cannot be expanded as a Fourier series. Since, tanx does not satisfy Dirichlet's conditions. [tanx has infinite number of infinite discontinuities.] 3. Find the sum of the Fourier series for Sol : See Page No. 2.20 4. If the Fourier series for the function Sol. Put x = π/2 is a point of continuity. 5. Find the constant term in the Fourier series corresponding to f(x) = cos2x expressed in the interval (— π, π). Sol. 6. Write a0, an in the expansion of x+x3 as a Fourier series in (-л, π). Sol. Let f(x) = x + x3 7. What are the constant term a0 and the coefficient of cos nx, an in the Fourier series expansion of f(x) = x − x3 in (−π, π) ? Solution : f(x) = x - x3 8. In the Fourier expansion of of bn, the coefficient of sin nx. Solution : ⸫ Given function is an even function. Hence, the value of bn = 0 9. If f(x) = x2 + x is expressed as a Fourier series in the interval (-2, 2) to which value this series converges at x = 2? Solution : x = 2 is a point of discontinuity in the extremum. 10. Find bn in the expansion of x2 as a Fourier Series in (-π, π). Solution : Given f (x) = x2 is an even function in the interval (-л, л) ⸫ n = 0 11. If f(x) is an odd function defined in (−l, l), what are the values of a0 and an? Solution : Given f(x) is an odd function in the interval (-l, l) ⸫ a0 = 0, an = 0 12. Find the Fourier constants b1 for x sin x in (-π, π). Solution: 13. If f(x) = Solution: 14. Determine the value of an, in the Fourier series expansion of f(x) = x3 in -л < x < л: Solution : 15. If f (x) = 2x in the interval (0, 4), then find the value of a2 in the Fourier series expansion. Solution: II. Problems under Half range series 1. Find half range sine series for f(x) = k in 0 < x < л. Solution: The sine series of ƒ (x) in (0, л) is given by 2.(a) Sketch the even and odd extension of the periodic function f(x) = x2 for 0 < x < 2 Solution : 2.(b) Sketch the graph of one even and one odd extension of f(x) = x3 in [0, 1] Solution : 3. The cosine series for f (x) = x sin x for 0 < x <л is given as Solution : 4. Expand f(x) = 1 in a sine series in 0 < x < л. Solution : The sine series of f(x) in (0, л) is given by 5. Find the Fourier sine series of f(x) = x in 0 < x < 2. Solution: In the interval 0 < x < 2 the half range sine series for 6. To which value, the half range sine series corresponding to f(x) = x2 expressed in the interval (0, 2) converges at x = 2? Sol. Given f(x) = x2 x = 2 is a finite point of discontinuity and also it is an end point. III. Problems under Parseval's identity, R.M.S value 1. State Parseval's identity for the half-range cosine expansion of f(x) in (0, 1). Solution: 2. Find the root mean square value of the function f(x) = x in the interval (0, l). Solution: 3. Define root mean square value of a function f(x) in a < x < b. Solution : Let f (x) be a function defined in an interval (a, b) then 4. What do you mean by Harmonic Analysis? Solution: The process of finding Euler constant for a tabular function is known as Harmonic Analysis. 5. Find the root mean square value of ƒ (x) = x (l − x) in 0 ≤ x ≤ l. Solution : 6. Define R.M.S value of a function ƒ (x) in c < x < c + 2l. Solution : 7. State TRUE or FALSE : Fourier series of period 20 for the function f(x) = x cos (x) in the interval (-10, 10) contains only sine terms. Justify your answer. Solution : TRUE. f (x) = x cosx is odd in (-10, 10) = 0 ⸫ a0 = 0 and an = 0 So, we get only sine terms.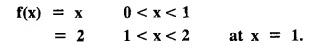
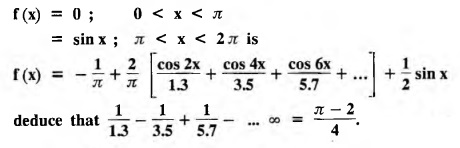
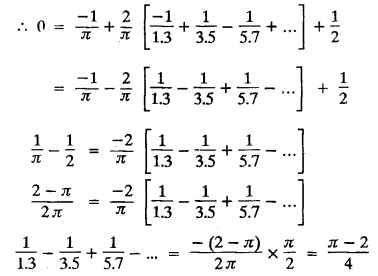
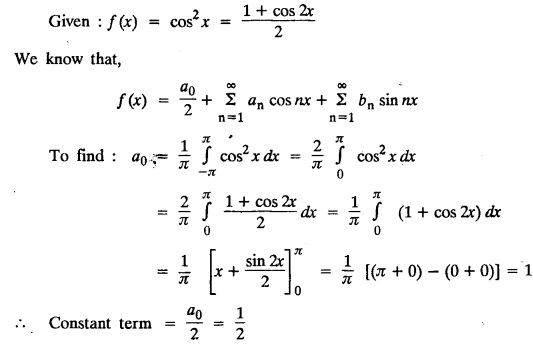
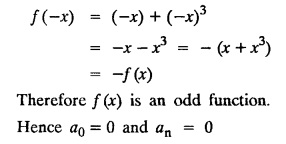
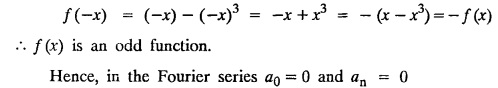
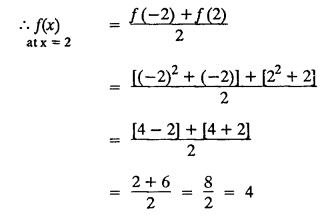
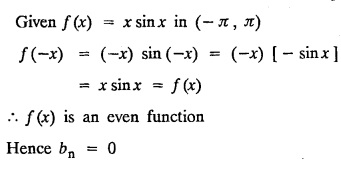
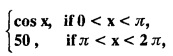 and f(x) = f (x + 2 л) for all x, find the sum of the Fourier series of ƒ (x) at x = π.
and f(x) = f (x + 2 л) for all x, find the sum of the Fourier series of ƒ (x) at x = π.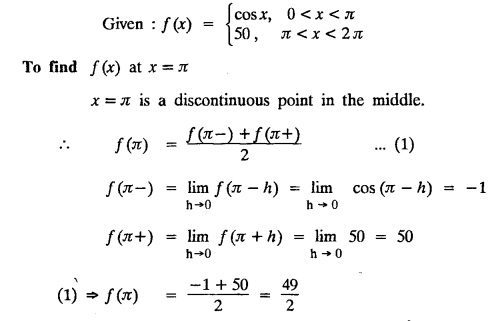
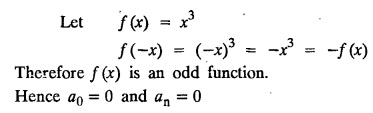
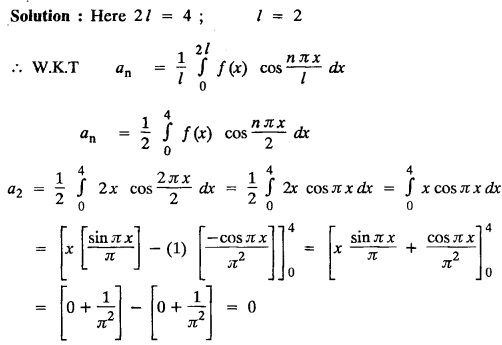
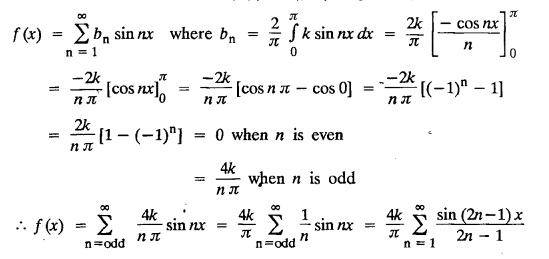
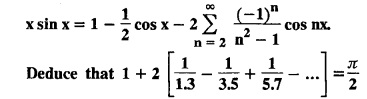
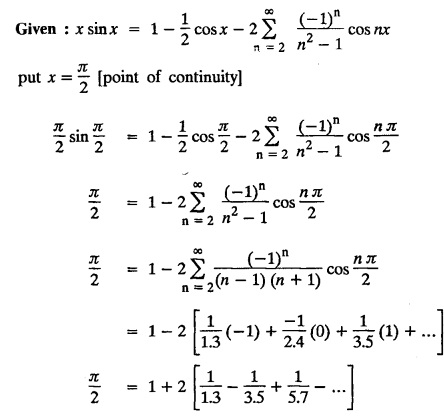
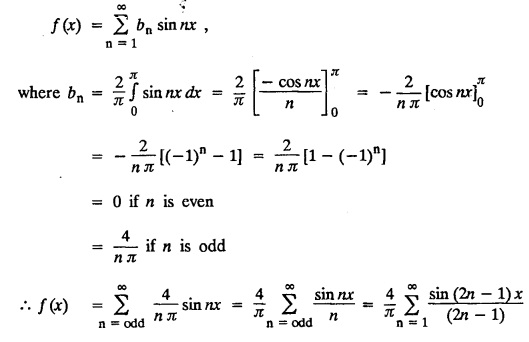
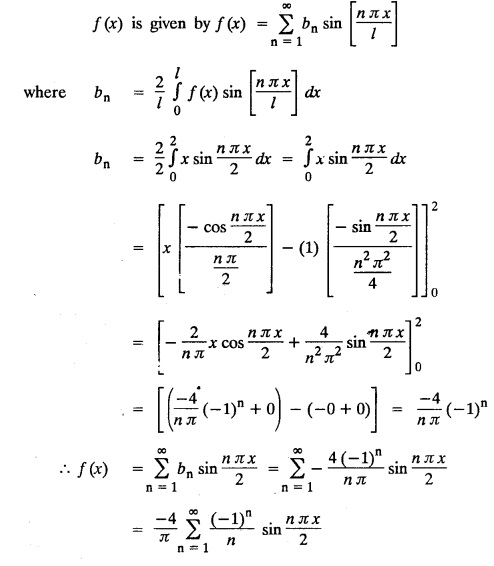
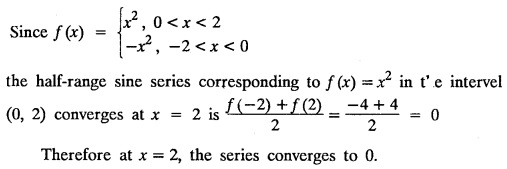
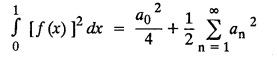
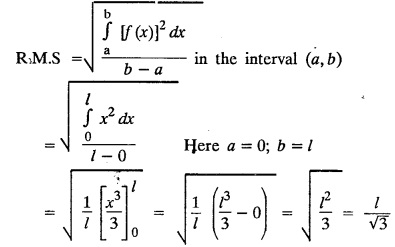


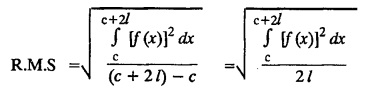
Transforms and Partial Differential Equations: Unit II: Fourier Series : Tag: : Fourier Series | Transforms and Partial Differential Equations - Questions and Answers
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
