Matrices and Calculus: Unit IV: Integral Calculus
Questions and Answers
Solved Problems | Integral Calculus | Matrices and Calculus | Matrices and Calculus
Questions and Answers: Matrices and Calculus: Integral Calculus
PART A QUESTIONS AND ANSWERS 1. Evaluate Ans: 2. Evaluate Ans: 3. Express Ans: 4. Express the integral Ans: 5. Evaluate Ans: 6. Ans: = 2 × 37 + 3 × 16 = 122 7. If Ans: 8. Express Ans: 9. Find the derivative of Ans: 10. Find Ans: 11. If y = Ans: 12. Find the fallacy Ans: 13. Evaluate Ans: 14. Evaluate Ans: 15. If Ans: 16. Ans: 17. Prove that Ans: 18. If In a = 2, ln b = −3 then find Ans: In ab2 = In a +2 ln b = 2 + 2(-3) = - 4 19. Evaluate Ans: 20. Evaluate Ans: 21. With a suitable substitution transformation the integral to one in the list of integrals? Ans: 22. If y = Ans: 23. If f(x) = 12, then, f' is continuous and Ans: 24. Evaluate Ans: 25. Verify by differentiation that the formula is correct Ans: We have to check it is correct or not by differentiation Differentiate w.r. to x, we get = cos x – sin2 x cos x = cos x (1 - sin2x) = cos x cos2x = cos3x, which is true ⸫ the given formula is correct 26. Evaluate Ans: 27. Evaluate Ans: 28. If f is continuous and Ans: 29. If ƒ is continuous on [a, b], then True or false Ans: False, we cannot bring variable out of the integral sign. 30. Ans: True 31. Ans: Since f(x) is not ≥ 0 ∀x ∈ [0, 2], we can not say it is the area under the curve. 32. Ans: True 33. Evaluate Ans: 34. Evaluate Ans: 35. Test the convergence of Ans: So, the integral is not convergent ⇒ it is divergent 36. Test the convergence of Ans: Hence, the integral is convergent 37. Indicate the type of improper integral and test its convergence Ans: ⸫ The integral is convergent. 38. Ans: False 39. Ans: It is improper integral of second kind or type. 40. Ans: Hence convergent True 41. Ans: 42. Evaluate Ans: 0 ⸪ sin3x cos2x is an odd function 43. Let f be a positive function Ans: 44. Suppose ƒ and g are continuous functions in (—∞, ∞) Ans: 45. Find the value of Ans: 46. Find Ans: ⸫ ƒ is even function 47. If Ans: 48. Find Ans: 49. Evaluate Ans: 50. Evaluate Ans: 51. Evaluate Ans: 52. Ans: Let t = sin θ – cos θ ⸫ dt = cos θ + sin θ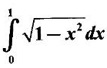 interpreting it in terms of area.
interpreting it in terms of area.
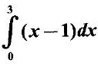 interpreting in terms of area.
interpreting in terms of area.
 in [2, 6], as a definite integral.
in [2, 6], as a definite integral.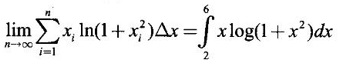
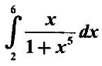 as limit of Riemann sum.
as limit of Riemann sum.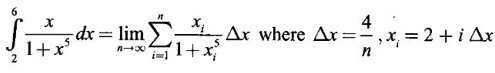
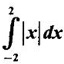 interpreting as area.
interpreting as area.
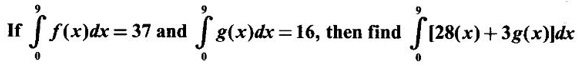
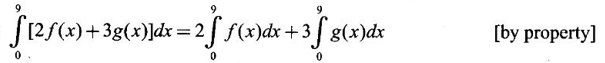
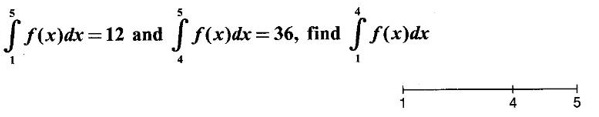
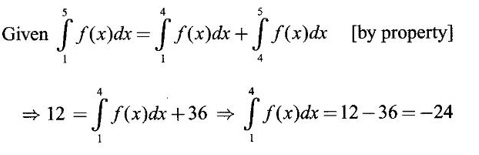
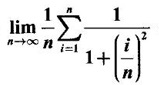 as definite integral
as definite integral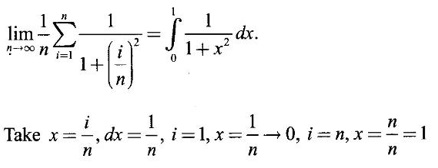
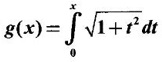
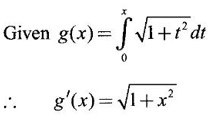
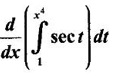
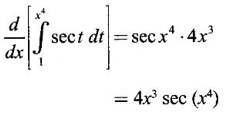
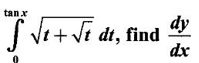
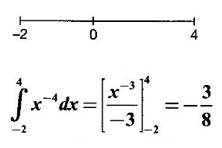

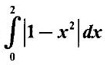
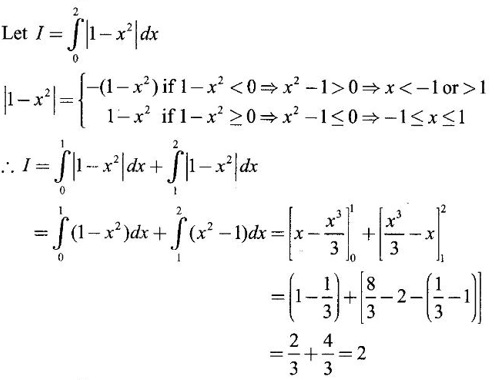
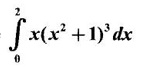
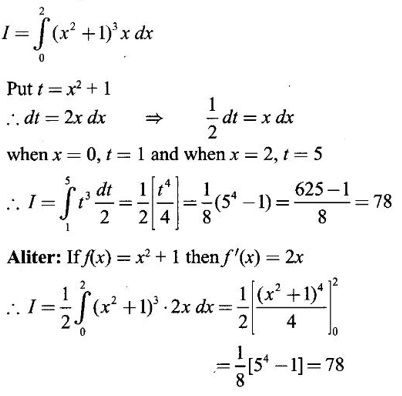
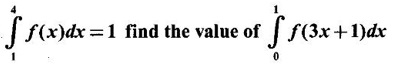
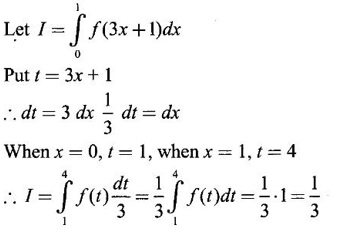


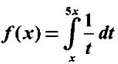 is a constant, find the constant
is a constant, find the constant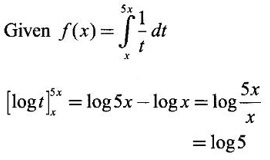
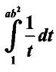
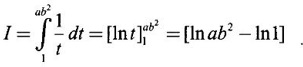
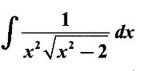
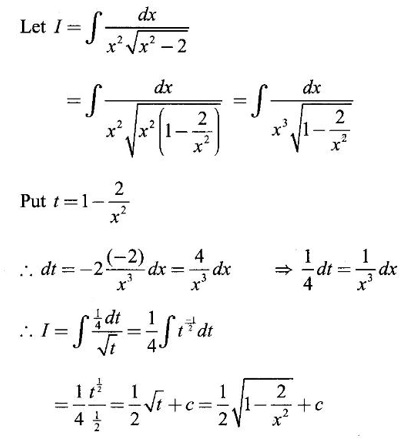
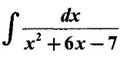
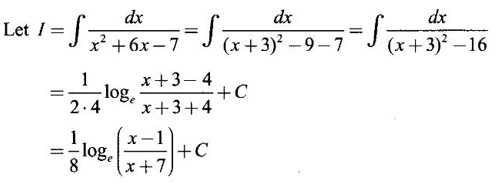
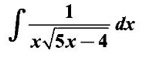
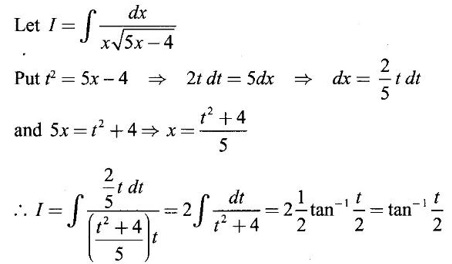
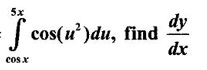
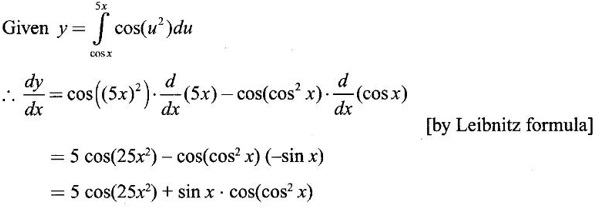
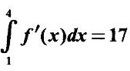 What is the value of f(4)?
What is the value of f(4)?
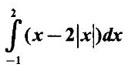
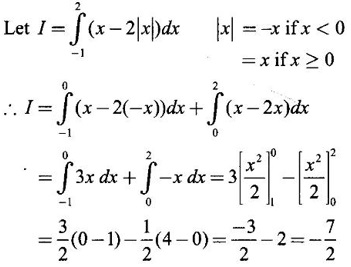
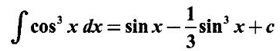
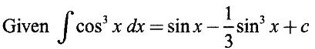
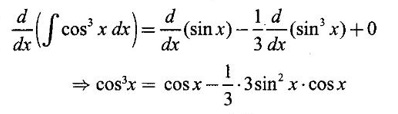
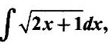 using a formula in the list (without substitution)
using a formula in the list (without substitution)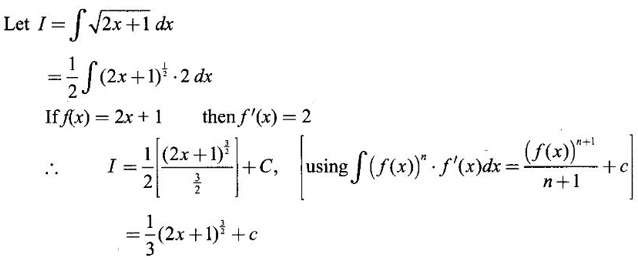
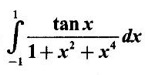
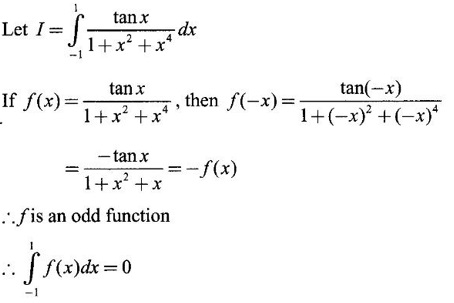

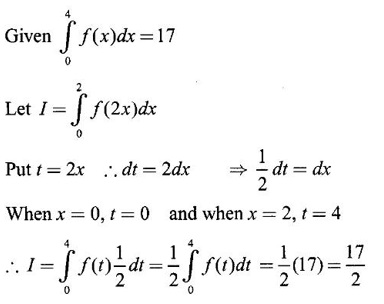
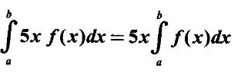
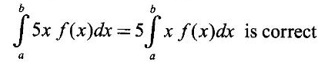
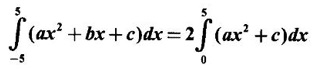 True or false
True or false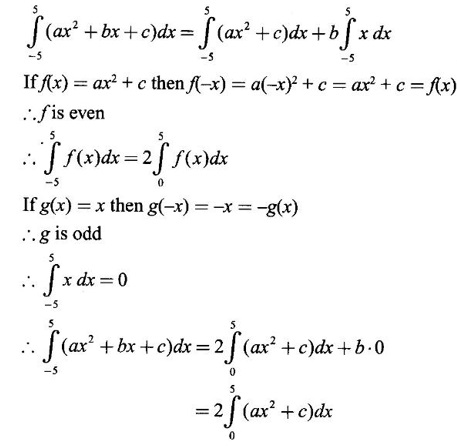
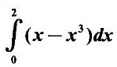 represents the area under the curve y = x − x2 True or false
represents the area under the curve y = x − x2 True or false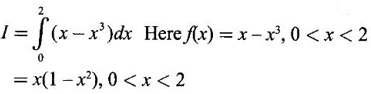
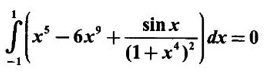 True or false
True or false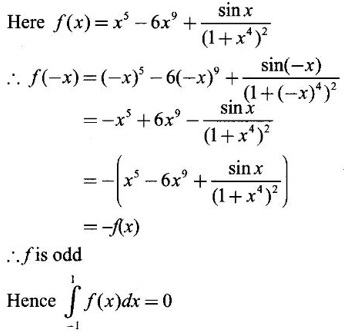
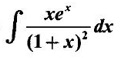

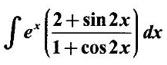
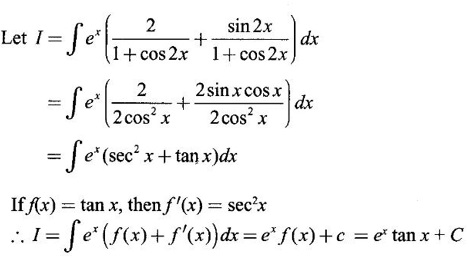
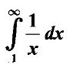
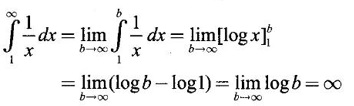
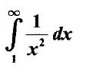
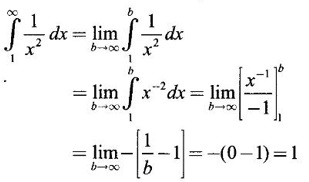
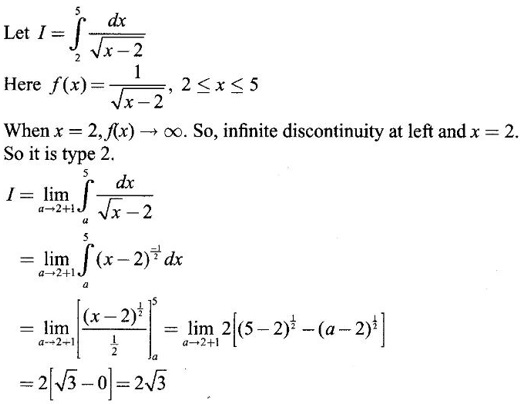
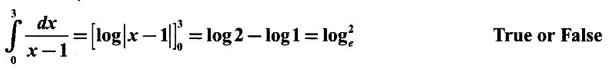

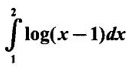 is a proper or improper integral? Why?
is a proper or improper integral? Why?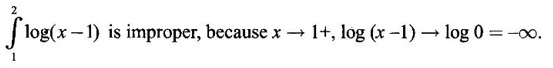




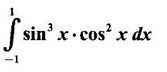
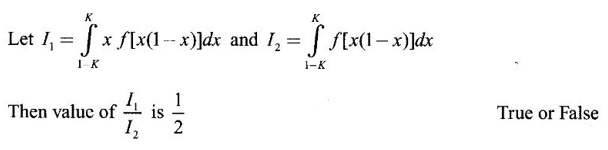
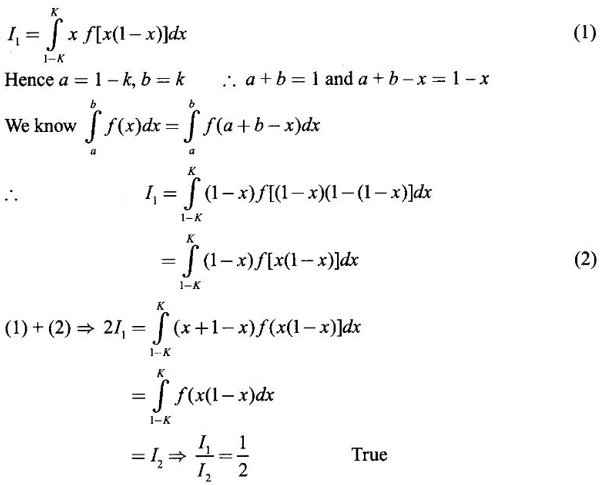
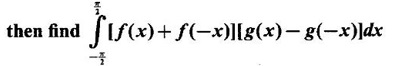

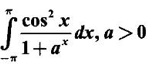

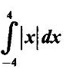

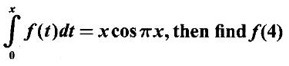
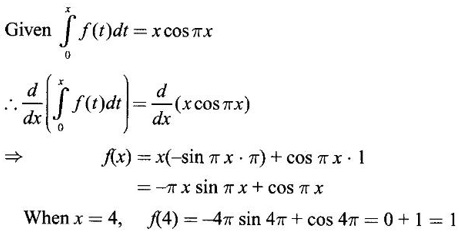
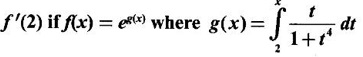
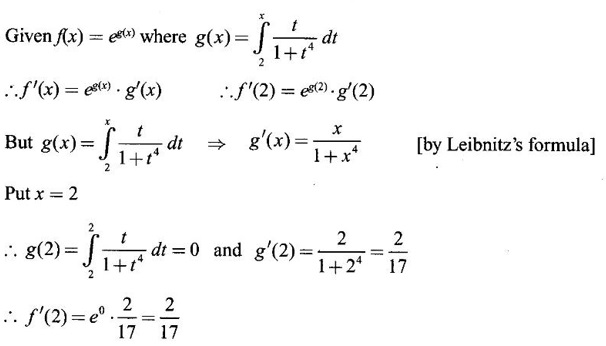
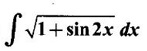
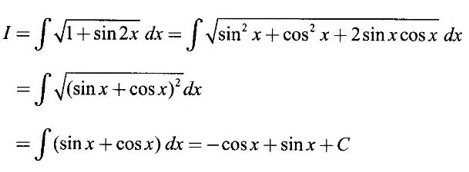
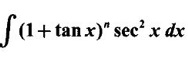
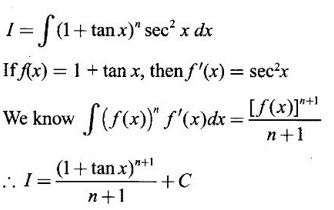
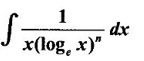
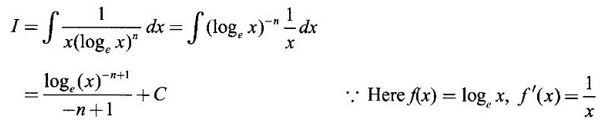
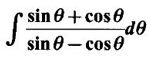
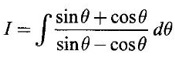
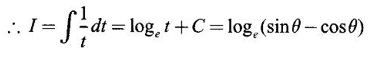
Matrices and Calculus: Unit IV: Integral Calculus : Tag: : Solved Problems | Integral Calculus | Matrices and Calculus | Matrices and Calculus - Questions and Answers
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
