Questions and Answers

PART A 

QUESTIONS AND ANSWERS

1.

Ans: 

2.

Ans: 

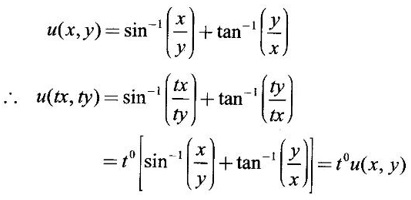
So, u(x, y) is homogeneous of degree 0.

So, by Euler's theorem

3.

Ans: 

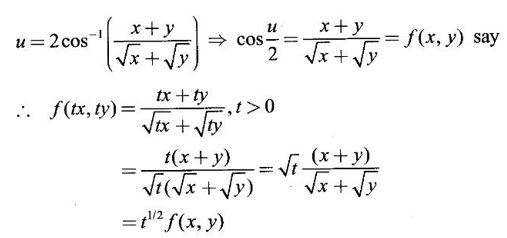
⸫ f(x, y) is a homogeneous of degree 1/2.

By Euler's theorem.

4.

Ans: 

Ans: Given z = f(x, y) and x and y are functions of u and v. So z is a composite function of u and v.

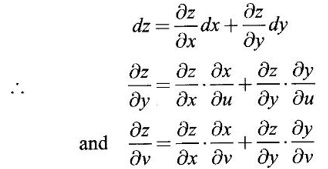
x = u - v,   y = uv

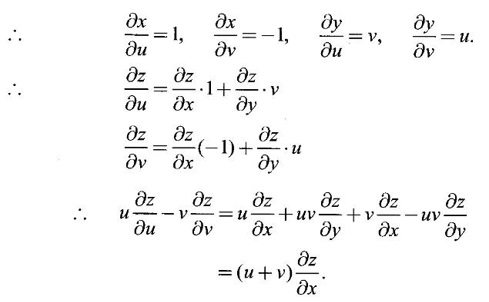
5.

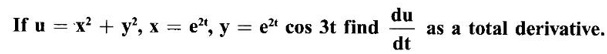
Ans:

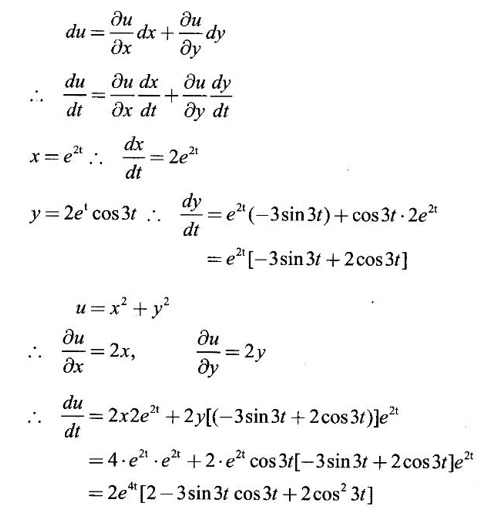
6. If u If u = f(x, y) and x = r + s, y = r - s prove that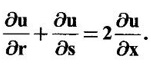

Ans: u is a composite function of r and s.

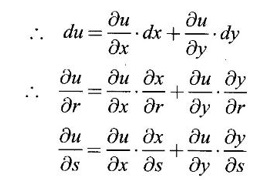
Given x = r + s and y = r - s

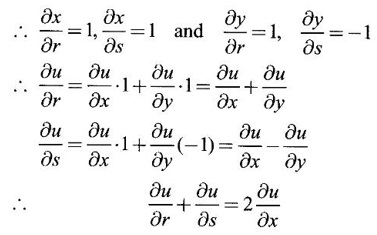
7.

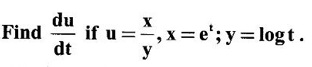
Ans:

We know that

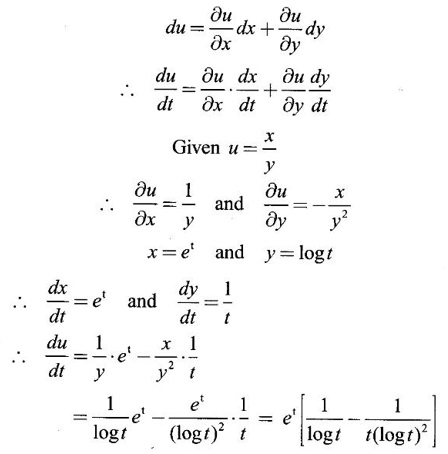
8.

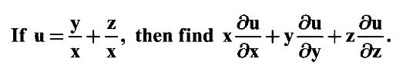
Ans:

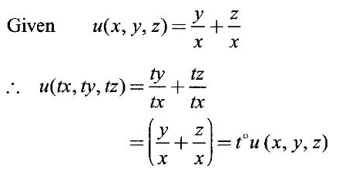
⸫ u(x, y, z) is homogeneous of degree 0.

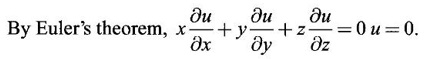
9. Find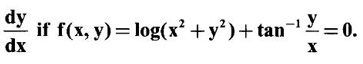

Ans: 

10.

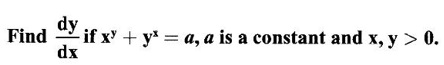
Ans: 

Given the implicit equation xy + yx = a

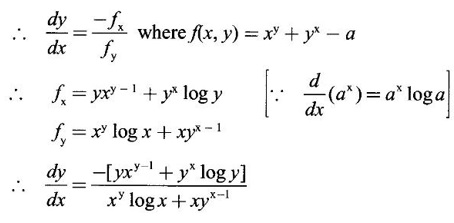
11.

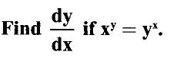
Ans: 

Given xy = yx ⇒ xy - yx  = 0 which is an implicit equation

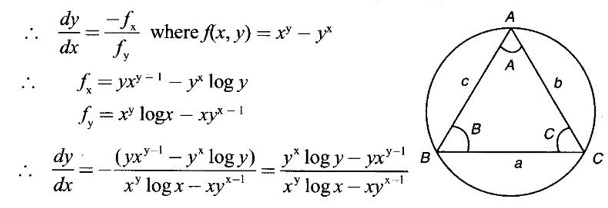
12.

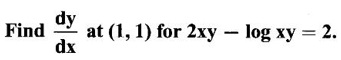
Ans: 

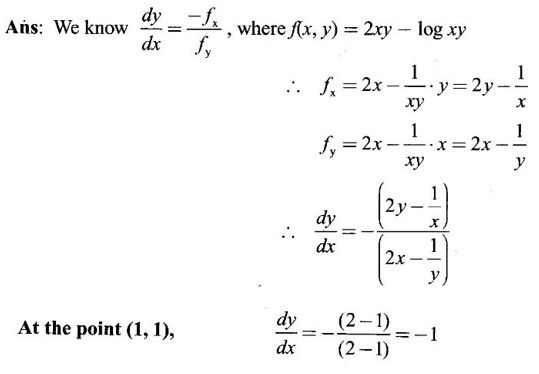
13.

Ans: Given x = r cos θ, y = r sin θ

⸫ r2 = x2 + y2

Differentiating partially w.r.to x

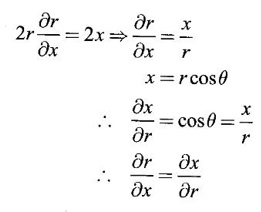
14.

Ans: 

15.

Ans: 

Given z = f(x + ay) + g(x − ay)

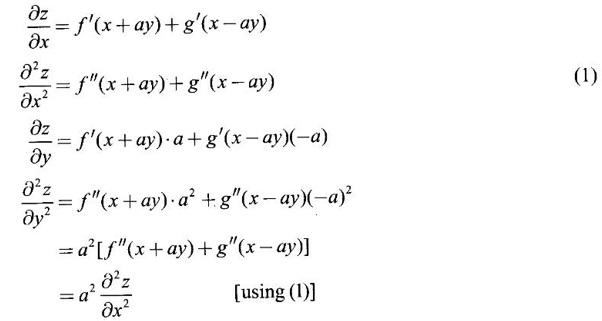
16.

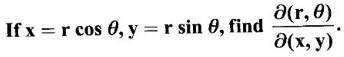
Ans: 

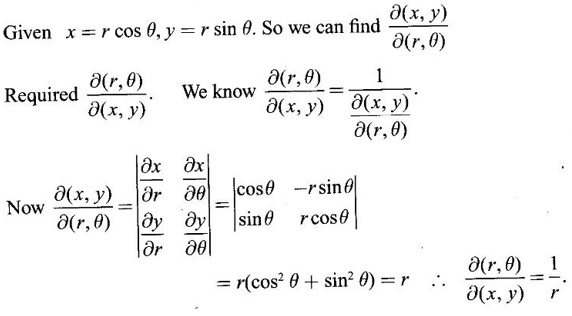
17.

Ans: 

Given u = x + y, y = uv

⸫ u = x + uv ⇒ x = u - uv

18.

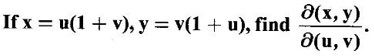
Ans:

Given x = u(1 + v)   y = v(1 + u)

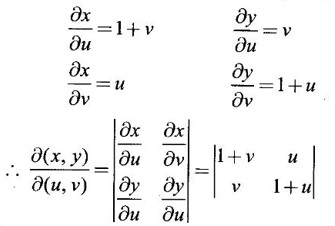
= (1 + u)(1 + v) - uv

= 1 + u + v + uv - uv

= 1 + u + v

19.

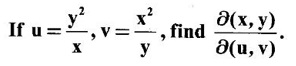
Ans:

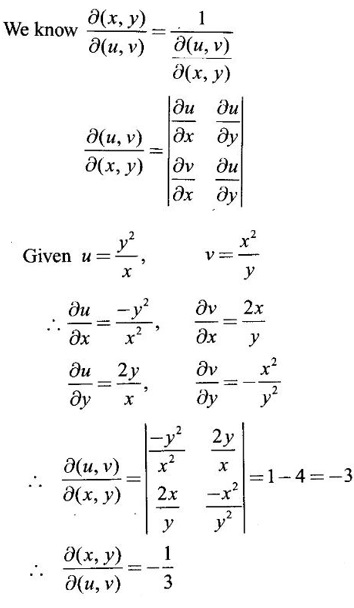
20.

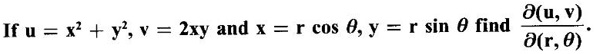
Ans:

Given u and v are functions of x, y and x and y are functions of r, θ. So, u, v are composite functions of r, θ.

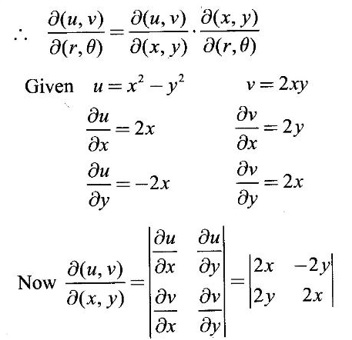
= 4x2 + 4y2

= 4(x2 + y2) = 4r2

Since x = r cos θ, y = r sin θ

21.

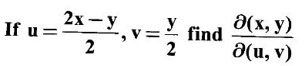
Ans: 

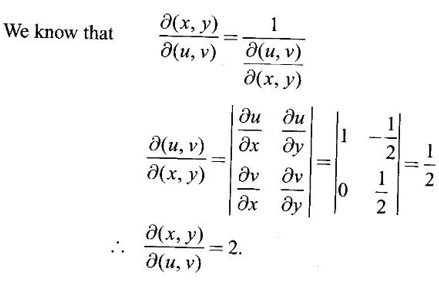
22. If x2y + 3y – 2 is expanded as Maclaurin's series, find the value at the point (1, 0).

Ans: 

Let f(x, y) = x2y + 3y – 2. Since f(x, y) is a polynomial in x and y, when it is expanded as a Maclaurin's series, we will get the same polynomial. 

⸫ f(1, 0) = −2.

23. Find the Taylor's series expansion of xy near the point (1, 1) upto first degree terms.

Ans: 

Given f(x, y) = xy

Taylor's expansion about (1, 1) is

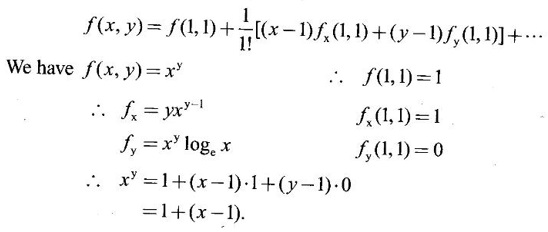
24. Evaluate [(1.03)1/3 + (0.98)1/4 −1] approximately using linear appropriation of Taylor's series.

Ans: 

Let ƒ(x, y) = x1/3 + y1⁄4 − 1.

Required value at the point (1.03, 0.98) which is close to (1, 1).

So we shall expand about (1, 1)

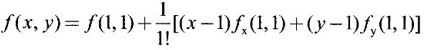is the linear approximation.

ƒ(1, 1) = 1 + 1 − 1 = 1

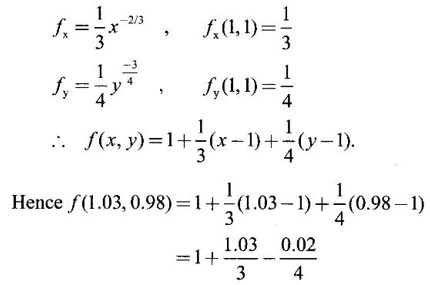
= 1 + 0.01– 0.005 = 1.005

25. Find the stationary points of f(x, y) = x2 − xy + y2 − 2x + y

Ans: 

Given f(x, y) = x2 − xy + y2 − 2x + y

Its stationary points are given by fx = 0, ƒy = 0

fx = 2x - y −2, fy = −x + 2y + 1

Solving 2x - y − 1 = 0 and -x + 2y + 1 = 0, we get

x = 1, y = 0

⸫ the stationary point is (1, 0)

26. Find the stationary points of f(x, y) = x3 + 3xy2 - 15x2 – 15y2 + 72x

Ans: 

Given f(x, y) = x3 + 3xy2 - 15x2 – 15y2 + 72x

The stationary points are given by ƒx = 0, ƒy = 0

Now ƒx = 3xy2 + 3y2 - 30x + 72

fy = 6xy - 30y

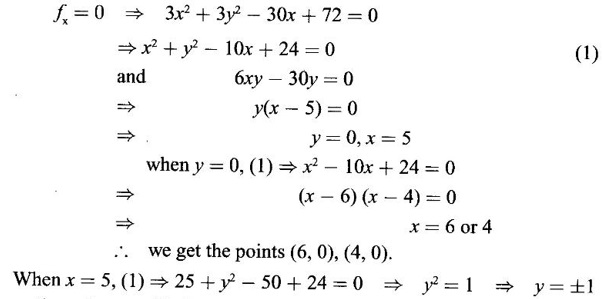
⸫ the points are (5, 1), (5, −1).

So, the stationary points are (6, 0), (4, 0), (5, 1) and (5, −1).

27. Find the maximum value of 3x2 - y2 + x3.

Ans:

Let f(x, y) = 3x2 - y2 + x3

28. State the necessary and sufficient condition for f(x, y) to have a relative maximum at (a, b).

Ans: 

The conditions are fx = 0, fy = 0 and rt - s2 > 0 and r < 0 at (a, b)

29. State the condition for the stationary point (a, b) of f(x, y) be a minimum.

Ans: 

At the point (a, b), rt - s2 > 0 and r < 0, where r = fxx, s = ƒxy, t = fyy

30. If (1, 1) is a stationary point of a function f(x, y) and if fxx = 6xy3, fxy = 9x2y, fyy = 6x3y, then find the nature of (1, 1).

Ans: At the point (1, 1), r = fxx = 6, s = fxy = 9, t = fyy = 6

⸫ rt - s2 = 6.6 - 92 < 0

⸫ (1, 1) is a saddle point.

31. Find the nature of the stationary point (0, −1) of the function f(x, y) if fxx = 4 - 12x2, fxy = 0, fyy = −4 + 12y2.

Ans: At the point (0, -1), r = fxx = 4

s = fxy = 0, t = fyy =  −4 + 12 = +8

⸫ rt - s2 = 32 > 0, r > 0

⸫ (0, -1) is a minimum point.

32. Using Euler's theorem, given u (x, y) is a homogeneous function of degree n, prove that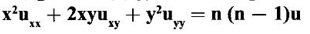

Ans: Refer Page No. 3.13

33. Using the definition of total derivative, find the value of du/dt, given u = y2 - 4ax, x = at2, y = 2at

Ans: 

Given u = y2 - 4ax; x = at2, y = 2at

So, u is a composite function of t.

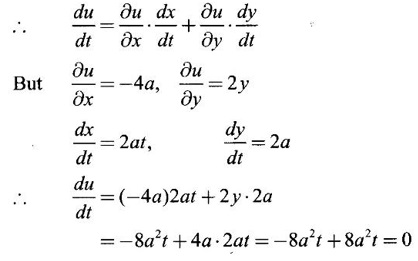
34.

Ans: Given u = x3y2 + x2y3 where x = at2, y = 2at

So, u is a composite function of t.

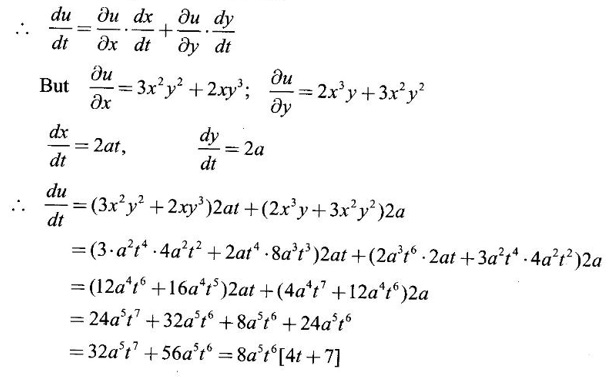
35.

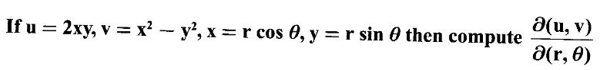
Ans: Refer Worked Example 6, Page No. 3.47

36.

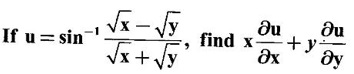
Ans: 

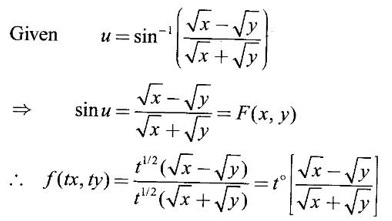
So, f(x, y) is a homogeneous of degree 0.

Hence, by Euler's theorem

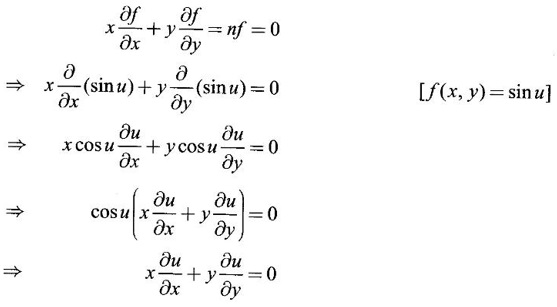
37.

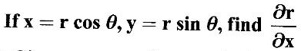
Ans: Given x = r cos θ, y = r sin θ

⸫ x2 + y2 = r2

Differentiating partially w.r.to ‘x'

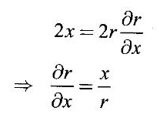
38. Find the minimum value of F = x2 + y2 subject to the constraint x = 1.

Ans: Given F = x2 + y2 and x = 1

⸫ F = 1 + y2

Differentiating w.r.to y,

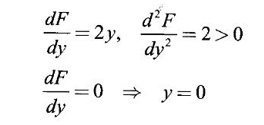
⸫ F is minimum at (1, 0) and minimum value of F = 1.

39.

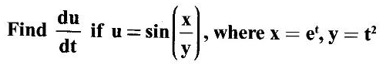
Ans: 

40.

Ans: 

41.

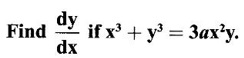
Ans: 

42. Find the stationary points of f(x, y) = x3 + y3 - 3x - 12y + 20

Ans: Given f(x, y) = x3 + y3 - 3x - 12y + 20

⸫ fx = 3x2 - 3

fy = 3y2 - 12

For a stationary point fx = 0 and fy =0

⸫ 3x2 – 3 = 0 ⇒ x2 = 1 ⇒ x = ±1

and 3 y2 – 12 = 0 ⇒ y2 = 4 ⇒ y = ±1

⸫ the stationary points are

(1, 2), (−1, 2), (1, −2), (−1, −2)

43.

Ans: 

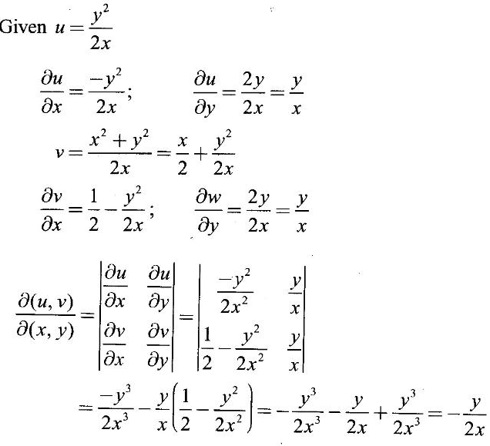
44.

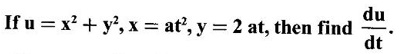
Ans: Given u = x2 + y2, x = at2, y = 2at u is a function of x, y and x, y are functions of t.