Matrices and Calculus: Unit II: Differential Calculus
Questions and Answers
Solved Problems | Differential Calculus | Matrices and Calculus
QUESTIONS AND ANSWERS: Matrices and Calculus: Differential Calculus
PART - A QUESTIONS AND ANSWERS 1. Find the domain of f(x) = Ans: Domain is the set of all real x for which f(x) is real ⸫ 1 - x2 ≥ 0 ⇒ x2 – 1 ≤ 0 ⇒ -1 ≤ x ≤ 1 ⸫ Df = [-1, 1] 2. Find the domain of the function f(x) = Ans: f(x) is real if x2 - 2x + 5 ≥ 0, since x2 + 1 ≠ 0 ∀ x∈ℝ For this quadratic, discriminant D = 4 - 4.5 = -16 < 0 ⸫ x2 - 2x + 5 ≥ 0 ∀ x∈ℝ Hence, Df = ℝ 3. Find the domain of Ans: f(x) is real if 1 – x > 0, 1 - x ≠ 1 and x + 2 ≥ 0 ⇒ x - 1 < 0, x + 1 and x + 2 ≥ 0 ⇒ x < 1 and x ≥ −2 ⇒ −2 ≤ x < 1, x ≠ 0 ⸫ Df = [−2, 0) ∪ (0, 1) 4. If f(x) = Ans: f(x) = 3√x - 2 5. If f(x) = Ans: f(x) = log(4 - x2) ⸫ Df is given by 4 − x2 > 0 ⇒ x2 − 4 < 0 ⇒ (x + 2)(x − 2) < 0 ⇒ -2 < x <2 ⸫ Df = (−2, 2) 6. Find the values of ƒ (0), ƒ (1), ƒ(1.5) Ans: When x = 0, ƒ(0) = |0 +1| = 1 When x = −1, ƒ(−1) = |−1+1| = 0 and when x = 1.5, ƒ(1.5) = |1.5 - 1| = |+0.5| = 0.5 7. Is the function in the question no.6 even? Ans: Hence, ƒ is even. 8. If f(x) = Ans: Hence, ƒ is odd 9. If Ans: 10. Ans: Hence, ƒ is odd ⸫ f(x) is even is false 11. If Ans: 12. If f(x) = x + 5, g(x) = x2 + 3 find f(g(0)) and ƒ(ƒ(−5)) Ans: 13. If then find g(f(3)) and g(f(2)). Ans: Put x = 3, then g(f(3)) = 3 − 2 = 1, Put x = 2, then g(f(2)) = 1 - 2 = −1 14. If f(f(x)) = x. Ans: Given f(x) = ⸫ f(f(x)) = x 15. If ƒ is an even function defined on [−5, 5] and if f(x) = Ans: Given f is an even function ⸫ There are 4 solutions in [-5, 5] 16. In the above problem if the interval is [−2, 2]. Find the number of solutions. Ans: Only 3 solutions belong to [−2, 2] 17. If f(x) = Ans: 18. Find the inverse of f(x) = x3 +1, x ∈ ℝ Ans: Given f(x) = x3 +1, x ∈ ℝ Clearly if x1 ≠ x2, then f(x1) ≠ f(x2) ⸫ f is one-one Let y = x3 + 1 ⇒ x3 = y – l ⇒ x = (y - 1)1/3 ⸫ The inverse is ƒ-1(y) = (y − 1)1/3, y∈ℝ or ƒ-1(x) = (x − 1)1/3, x∈ℝ 19. Find the inverse of f(x) = Ans: Clearly f is one-one 20. Prove that the inverse of Ans: 21. If Ans: Given f(x) = cos[π2]x + cos[-π2]x We know π = 3.14 (approximately). ⸫ π2 = 9.9 (approximately) 22. Find the vertical asymptote of the graph of the function Ans: 23. Find Ans: 24. Ans: Hence, we can not write as difference of limits. 25. Evaluate Ans: 26. Ans: 27. The equation x10 - 10x2 + 5 = 0 has a root in the interval (0, 2) True or false. Ans: Let f(x) = x10 - 10x2 + 5. It is continuous in (0, 2). ƒ(0) = 5 > 0 and f(1) = 1 − 10 + 5 = −4 < 0 Since ƒ(0) and ƒ(1) have opposite signs, there is a root between 0 and 1. Hence there is a root in (0, 2) – True 28. Ifƒ'(r) exists, then Ans: True, since differentiability ⇒ continuity 29. Find the expression for the function whose graph is the line segment joining the points (-5, 10) and (7,−10) Ans: Equation of the line joining the points(-5, 10) and (7, −10) is 30. Find Ans: We know 180° is π radian 31. Find Ans: 32. Find Ans: Hence, f is continuous at x = 1. 32. Ans: 33. If Ans: 34. If ƒ and g are are continuous functions with f(3) = 5 and Ans: Given ƒ and g are continuous 35. Ans: 36. If ƒ is an odd function and if Ans: 37. Test the continuity of the function Ans: Hence, ƒ is continuous at x = 0 and hence, ƒ is continuous ∀x. 38. Find the value of a Ans: g is continuous at x = 2 39. Ans: Given f is continuous at x = 0 40. If Ans: 41. Ifƒ'(2) = 4, g(3) = 6 and g′(3) = 5 find h'(3) if h(x) = Ans: 42. If f(x) = mx + c and ƒ(0) = ƒ'(0) = 1, then what is ƒ'(2) ? Ans: f(x) = mx + c ⸫ f'(x) = m f'(0) = 1 ⇒ m = 1 Hence, f'(x) = 1 ⸫ ƒ'(2) = 1 43. At what point on the curve y = [In (x + 4)]2 is the tangent horizontal? Ans: ⸫ the point is (−3, 0) 44. Ans: Let ƒ(x) = |x2 + x| 45. If the line x + y = a is a tangent to the curve Ans: The line x + y = a ⇒ y = a - x will touch if it intersects the ellipse in coincident points. The point of intersection are given by 46. If the normal to the curve y = f(x) at the point (3, 4) makes an angle Ans: f'(3) is the slope of the tangent at (3, 4) on y = f(x) Given normal at (3, 4) makes angle of 3π/4 ⸫ Slope of the normal = tan 3π/4 = -1 47. If the tangent to the curve y = f(x) at the point (4, 3) passes through the point (0, 2), then find the value of ƒ' (4). Ans: Slope of the tangent at (4, 3) on y = f(x) is ƒ'(4) since the tangent passes through (0, 2). ƒ'(4) = slope the line joining the points (4, 3) and (0, 2). 48. At what point on the curve y = ex, the tangent line is parallel to y = 2x? Ans: ⸫ the point is (loge 2,2) 49. Ans: Hence, f(x) changes from positive to negative as x increases in a ngd. Of 1/4 ⸫ ƒ has max at x = 1 / 4 50. Find the absolute maximum of f(x) = Ans: ƒ'(0) does not exist ⸫ x = 0 is a critical point Note that the absolute minimum is f(0) = 0, at the critical point x = 0 51. Determine the critical points of the function Ans: g'(x) does not exist when x = 0 or 2; which are the end points and so not 1 critical points. So the only critical point is x = 1 [Note that initial points are interior points of the domain] 52. If an odd function ƒ has a local minimum at x = e, then what can you say about the value of ƒ at x = −e. Ans: At x = -e, the function has an local maximum 53. Find the maximum value of the product of two numbers whose sum is 12. Ans: Let x; y be the numbers x + y = 12 ⇒ y = 12 - x P = xy = x(12 - x) = 12x - x2 ⸫ Maximum value = 6⸱6 = 36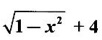
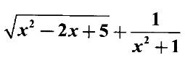
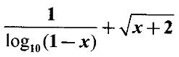
 then find the domain of
then find the domain of 

 find the domain of fg and
find the domain of fg and ![]()



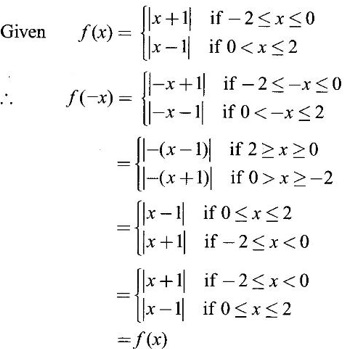
 − Test ƒ is even or odd
− Test ƒ is even or odd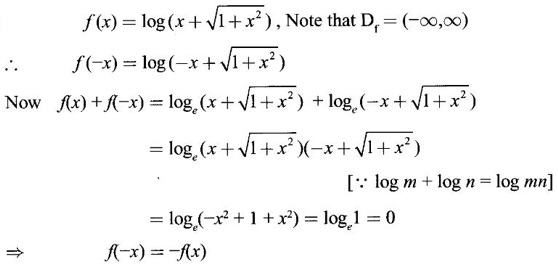
 then ƒ is even - True or False.
then ƒ is even - True or False.
 is even, True or False
is even, True or False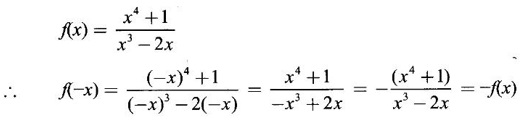
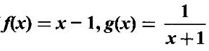 then find f(g(2)) and g(f(2))
then find f(g(2)) and g(f(2))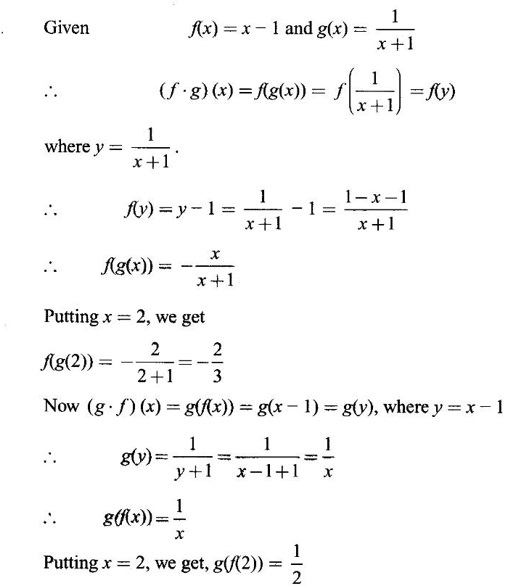
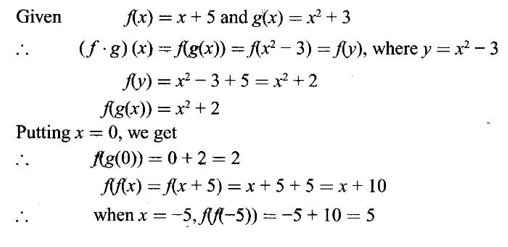


 where a > 0 and is a positive integer, show that
where a > 0 and is a positive integer, show that
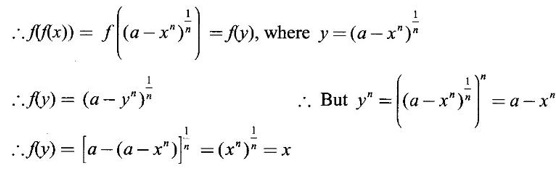
 find the number of solutions of this equation in [−5, 5].
find the number of solutions of this equation in [−5, 5].
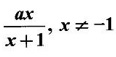 then for what values of a, f(f(x)) = x?
then for what values of a, f(f(x)) = x?
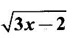
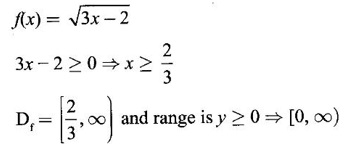
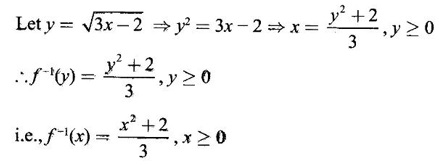


 where [x] is the greatest integer ≤ x, then find the values of
where [x] is the greatest integer ≤ x, then find the values of 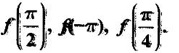




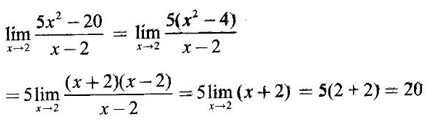
 is not true, why?
is not true, why?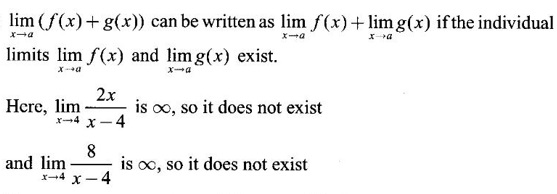

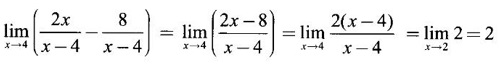
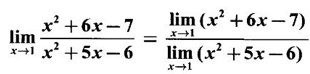 is not true. Why?
is not true. Why?
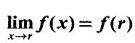 True or false
True or false
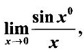 means x degrees.
means x degrees.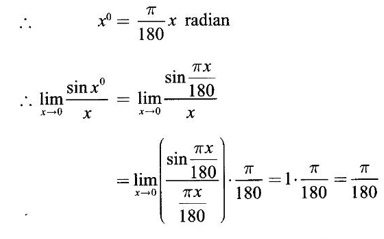
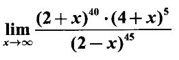
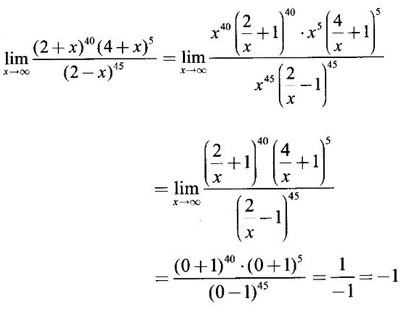


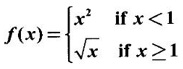
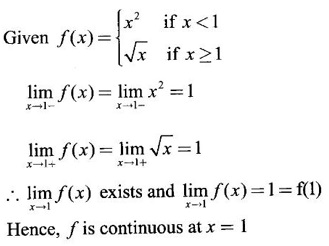
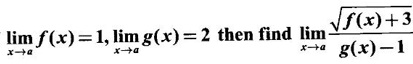
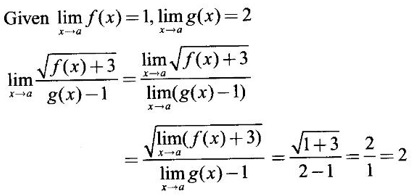


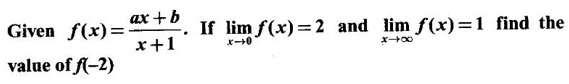
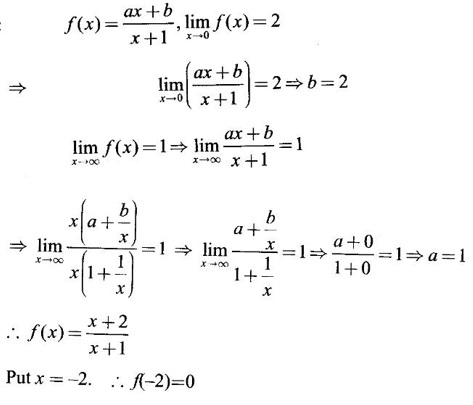
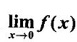 exists, find its value.
exists, find its value.
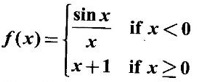

 is continuous at x = 2
is continuous at x = 2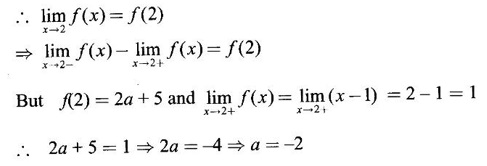
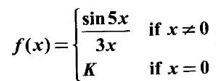 If ƒ is continuous at x = 0, find K.
If ƒ is continuous at x = 0, find K.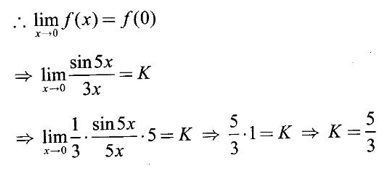
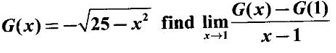
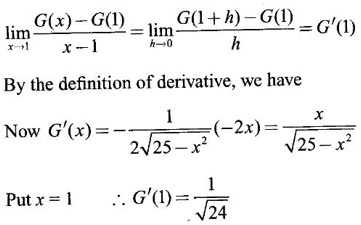


 true or false
true or false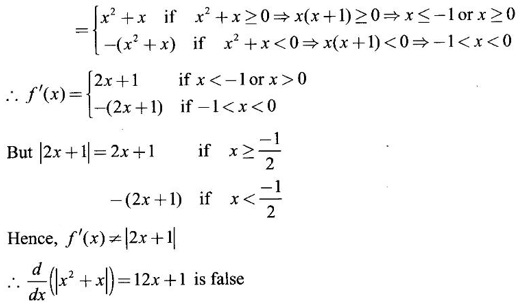
 then find the value of a
then find the value of a
![]() with the positive x-axis, then find the value of ƒ’(3).
with the positive x-axis, then find the value of ƒ’(3).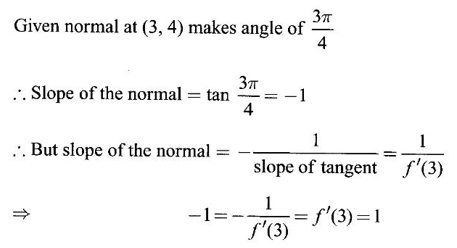

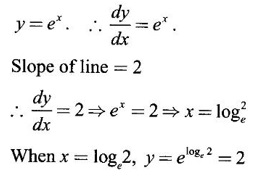
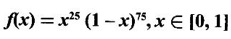 Find the point at which f(x) is maximum.
Find the point at which f(x) is maximum.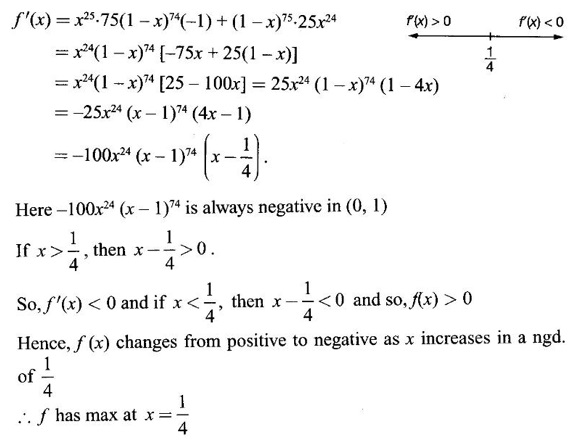

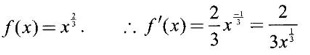
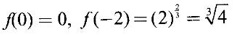
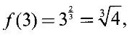 which is the absolute maximum at the end point x = 3.
which is the absolute maximum at the end point x = 3.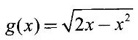
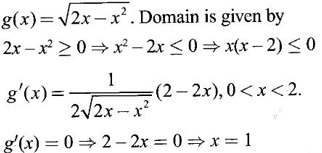
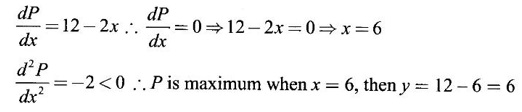
Matrices and Calculus: Unit II: Differential Calculus : Tag: : Solved Problems | Differential Calculus | Matrices and Calculus - Questions and Answers
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
