Matrices and Calculus: Unit I: Matrices
Questions and Answers
Solved Example Problems | Matrices
Questions and Answers : Matrices and Calculus: Matrices
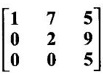
PART A QUESTIONS AND ANSWERS 1. If A = Ans: Characteristic equation of A is |A - λI| = 0 ⇒ λ2 - 7λ + 6 = 0 ⇒ (λ − 6)( λ - 1) = 0 ⇒ λ = 6,1. ⸫ the eigen values of A2 - 2A + I are 62 −2·6 + 1, 12 − 2 · 1 + 1 ⇒ 25, 0 2. Prove that Ans: Characteristic equation of A is |A - λI| = 0 Hence the eigen values of A and −3A-1 are the same. 3. Two eigen values of the matrix A = Ans: Given two eigen values of A are 1, 1. Let λ be the third eigen value. ⸫ 1 + 1 + λ = 2 + 3 + 2 ⇒ λ = 5 ⸫ the eigen values of A are 1, 1, 5 ⸫ the eigen values of A-1 are 1, 1, 1/5 4. If the product of two eigen values of the matrix A = Ans: Let λ1, λ2, λ3 be the eigen values of A. Given λ1λ2 = 2. We know λ1λ2 λ3 = |A|=8 ⸫ 2λ = 8 ⇒ λ3 = 4. 5. Find the sum and product of the eigen value of the matrix Ans: Sum of the eigen values = 2 + 2 + 2 = 6 Product of the eigen values = |A| = 2(4 − 0) + 1(−2) = 6 6. If the sum of two eigen values and trace of a 3 × 3 matrix A are equal, find the value of |A|. Ans: Let λ1, λ2, λ3 be the eigen values of A Then λ1 + λ2 + λ3 = trace of A But, given λ1 + λ2 = trace of A ⸫ λ1 + λ2 + λ3 = λ1 + λ2 ⇒ λ3 = 0 ⸫ |A| = λ1 λ2 λ3 = 0 7. Find the constants a and b such that the matrix Ans: Let A = Given eigen values are 3, -2 But the eigen values of A are a and b 8. Two eigen values of A = Ans: Let the third eigen value be λ. Then the other two eigen values are 2λ, 2λ ⸫ 2 λ + 2λ + λ = 4 + 3 + (−2), ⇒ 5λ = 5 ⇒ λ = 1 ⸫ eigen values of A are 2, 2, 1 ⸫ eigen of A2 are 22, 22, 12 ⇒ 4, 4, 1. 9. If λ1, λ2, …, λn are the eigen values of an n × n matrix A, then show that λ13, λ23, …, λn3 are the eigen values of A3. Ans: Let λ be any eigen value of A. Then we can find a column matrix X ≠ 0 such that ⸫ λ3 is an eigen value of A3, by definition. This is true for all eigen values of A. ⸫ λ13, λ23, …, λn3 are eigen values of A3. 10. If the eigen values of a 3 × 3 matrix A are 2, 3, 4, find the eigen values of adj A. Ans: The eigen values of A are 2, 3, 4 ⸫ the eigen values of A-1 are 11. The matrix A = Ans: Let λ be the eigen value of A for which X = Then (A - λ I)X = 0 ⸫ Corresponding eigen value is -2. 12. Using Cayley-Hamilton theorem find the inverse of Ans: Let A = The characteristic equation of A is |A – λI| = 0 ⇒ λ2 - 4λ – 5 = 0 (1) By Cayley-Hamilton theorem A satisfies (1) ⸫ A2 - 4A – 5I = 0 ⇒ 5I = A2 - 4A Multiply by A-1, 5 A-1 = A - 4 A-1A = A – 4I 13. If 2, 3 are eigen values of a square matrix A of order 2, express A2 in terms of A and I. Ans: Given eigen values of A are 2, 3. The characteristic equation of A is λ2 - S1λ + S2 = 0 where S1 = sum of the diagonal elements = sum of eigen values = 2 + 3 = 5 S2 = |A| = 2 ⋅ 3 = 6 ⸫ the characteristic equation is λ2 - 5 λ + 6 = 0 A satisfies it, by Cayley-Hamilton theorem ⸫ A2 - 5A + 6I = 0 ⇒ A2 = 5A – 6I 14. If A is an orthogonal matrix, show that A-1 is also orthogonal. Ans: Given A is orthogonal. ⸫ AT = A-1 = B, say then BT (A-1)T = (AT)-1 ⇒ BT = B-1 ⸫ B is orthogonal i.e., A-1 is orthogonal. 15. Find the nature of the quadratic form 2x2 + 2xy + 3y2. Ans: Matrix of the quadratic form is A = The principal minors are D1 = 2 > 0, D2 = |A| = 5 > 0 ⸫ the Q.F is positive definite. 16. If the quadratic form ax2 + 2bxy + cy2 is positive definite (or negative definite) then prove that the quadratic equation ax2 + 2bx + c = 0 has imaginary roots. Ans: The matrix of the quadratic form is A = Then the principle minors are D1 = a, D2 = |A| = ac – b2 If the quadratic form is positive definite then D1 > 0 and D2 > 0 17. Find the nature of the quadratic form 2x1 x2 + 2 x1 x3 - 2 x2 x3. Ans: The matrix of the Q.F is A = The principle minors are D3 = |A| = -2 < 0 ⸫ the quadratic form is indefinite. 18. Find the index and signature of the quadratic form x12 + 2x22 - 5x32. Ans: Since only square terms are there, it is in canonical form λ1 = 1, λ2 = 2, λ3 = −5 ⸫ Index = number of +ve eigen values = 2 Signature = difference between the number of positive and negative eigen values = 2 – 1 = 1 19. What is the sum of the squares of the eigen values of Ans: We know the eigen values of a triangular matrix are the diagonal elements of the matrix. ⸫ the eigen values are 1, 2, 5 ⸫ sum of the squares = 12 + 22 + 52 = 30 20. Write down the matrix of the quadratic form 2x2 + 0y2 + 8z2 + 4xy + 10xz – 2yz. Ans: The given quadratic form is 21. For a given matrix A of order 3, │A│= 32 and two of its eigen values are 8 and 2. Find the sum of the eigen values Ans: Given |A| = 32 and two of the eigen values are 8 and 2. Since A is a 3 × 3 matrix, it has another eigen value. Let it be λ. We know product of the eigen values = |A| But |A| = 32 ⇒ 8.2λ = 32 ⇒ λ = 2 22. Check whether matrix B is orthogonal? Justify. Ans: Given B = BBT = BTB = I ⸫ B is orthogonal. 23. Use Cayley-Hamilton theorem to find A4 – 4A3 - 5A2 + A + 2I when Ans: Given A = ⸫ characteristic equation is |A-λI| = 0 24. True or false: If A and B are two invertible matrices then AB and BA have the same eigen values. Ans: True. Given A and B are invertible. ⸫ A-1 and B-1 exist. Now A-1 (AB)A = (AA-1)BA = IBA = BA. So, AB and BA are similar. We know that similar matrices have the same eigen values. ⸫ AB and BA have same eigen values. 25. If the sum of the eigen values of the matrix of the quadratic form is equal to zero, then what will be the nature of the quadratic form? Ans: If the quadratic form is in two variables, then the matrix of the quadratic form is a 2 × 2 matrix. Let λ1, λ2 be the eigen values. If λ1 + λ2 = 0, then λ1 and λ2 have opposite signs. So, the quadratic form is indefinite. 26. A is a singular matrix of order three, 2 and 3 are the eigen values. Find the third eigen value. Ans: A is 3 × 3 matrix. Given |A| = 0 and 2 and 3 are two eigen values. Let λ3 be the third eigen value. But the product of the eigen values = |A| = 0 ⇒ 2 × 3 × λ3 = 0 ⇒ λ3 = 0 27. Find the eigen vector corresponding to the eigen value 1 of the matrix Ans: Given 1 is the eigen value of the matrix Let 28. Find the sum and product of the eigen values of the matrix Ans: Sum of the eigen values = Sum of the diagonal elements of A = 1 + 0 - 3 = -2 Product of the eigen values = |A| = − 1(−6 − 2) − 3(−1 + 4) [expanding by the second row] = 8 – 9 = -1 29. Find the nature of the quadratic form 2x12 – x22. Ans: Q.F is 2x12 – x22 Since only square terms are there, it is in Canonical form. There are positive and negative terms and hence the Q.F is indefinite. 30. If 2 is an eigen value of A = Ans: Given 2 is an eigen value of A. Let λ2, λ3 be the other eigen values of A. ⸫ 2 + λ2 + λ3 = Sum of the diagonal elements of A. ⇒ 2 + λ2 + λ3 = 2 + 1 − 1 ⇒ λ2 + λ3 = 0 ⇒ λ2 = - λ3 (1) We have 2 λ2 λ3 = |A| ⸫ the other two eigen values are -2, 2 31. Discuss the nature of the following quadratic form 3x12 + 3 x22 - 5 x32 - 2x1x2 − 6 x1x2 − 6 x3x1. Ans: The matrix of the Q.F is A = The principal minors are D1 = 3 > 0, = 3(−15+9) +1(5 −3) + (−3)(−3 + 3) = -18 + 2 + 0 = -16 < 0 Since D1 > 0, D2 > 0 and D3 < 0, the Q.F is indefinite. 32. Two of the eigen values of A = Ans: Let λ1, λ2, λ3 A, be the three eigen values of A. Let λ1 = 3, λ2 = 6 ⸫ λ1 + λ2 + λ3 = Sum of the diagonal elements of A. ⇒ 3 + 6 + λ3 = 3 + 5 + 3 ⇒ λ3 = 2 ⸫ the eigen values of A are 2, 3, 6. Hence the eigen values of A-1 are ½, 1/3, 1/6 33. Find the sum of the squares of the eigen values of the matrix Ans: Since A is upper triangular matrix, the eigen values are the diagonal elements of A. i.e., the eigen values of A are 1, 2, 5. ⸫ sum of the squares of the eigen values = 12 + 22 + 52 = 30 34. State the nature of quadratic form 2xy + 2yz + 2zx. Ans: The matrix of the quadratic form is A = Since D1 = 0, D2 < 0, D3 > 0, the nature of the quadratic form is indefinite. 35. Write down the matrix of the quadratic form Q(x, y) = 3x2 + 2y2 - 4xy. Ans: The quadratic form is 3x2 + 2y2 - 4xy ⸫ the matrix of the quadratic form is A = 36. Two eigen values of matrix A = Ans: Given two eigen values are 3 and 0. Let λ be the third eigen value then λ + 3 + 0 = 8 + 7 + 3 ⇒ λ = 15. 37. If the eigen values of the matrix A of order 3 × 3 are 2, 3, and 1, then find the eigen values of adjoint A. Ans: Given the eigen values of a matrix A are 2, 3, 1. But |A| = product of eigen values = 2 × 3 × 1 = 6 Eigen values of A-1 are 1/2, 1/3, 1 ⸫ Eigen values of adj A = 38. If λ is the eigen values of the matrix A then prove that λ2 is the eigen value of A2. Ans: Given λ is the eigen value of A, then there exists a non zero column matrix X such that AX = λX ⇒ A2X = A(AX) = A(λX) = λ (AX) = λ (λX) = λ2X ⸫ λ2 is the eigen of value of A2. 39. Write down the matrix corresponding to the quadrate form 2x12 + 5x22 + 4x1x2 + 2x3x1 Ans: Given quadratic form is 2x12 + 5x22 + 4x1x2 + 2x3x1. The matrix of the quadratic form is A = 40. What is the nature of the quadratic form x2+ y2 + z2 in four variables? Ans: The quadratic form in four variables is x2+ y2 + z2 + 0 ⋅ w2 ⸫ the nature of quadratic form is positive semi-definite 41. Find the Eigen values of 3A +2I, where A = Ans: Given A = Since A is Lower triangular matrix, the eigen values are the diagonal elements of A. The eigen values of A are 2, 5. The eigen values of I are 1, 1. ⸫ the eigen values of 3A +2I are 3⸱2 + 2 ⸱1, 3⸱5 + 2⸱1 = 8, 17 42. Give the nature of a quadratic form whose matrix is Ans: Since the given matrix its eigen values are −1, −1, −2 and they are all negative. ⸫ the quadratic form is negative definite. 43. If 2, 3 are the eigen values of Ans: Let A = Given 2 and 3 are two eigen values of A. Let λ1 = 2 and λ2 = 3 We know λ1 + λ2 + λ3 = 2 + 2 + 2 = 6 2 + 3 + λ3 = 6 ⇒ λ3 = 6 – 5 = 1 6 = 8 - 2b ⇒ -2b = -2 ⇒ b = 1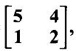 find the eigen values of A2 - 2A + I.
find the eigen values of A2 - 2A + I.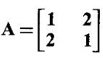 and -3A-1 have the same eigen values.
and -3A-1 have the same eigen values.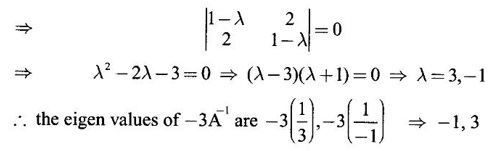
 are equal to 1 each, find the eigen values of A-1.
are equal to 1 each, find the eigen values of A-1.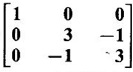 is 2, find the third eigen value.
is 2, find the third eigen value.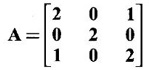
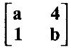 has 3 and -2 as eigen values.
has 3 and -2 as eigen values.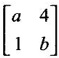
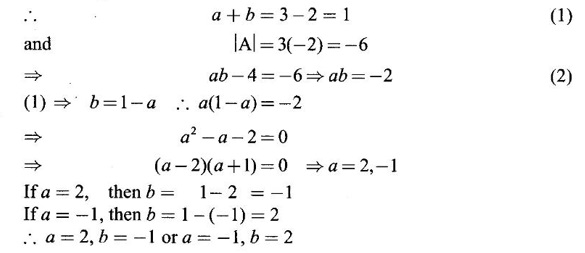
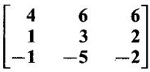 are equal and they are double the third. Find the eigen values of A2.
are equal and they are double the third. Find the eigen values of A2.
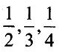
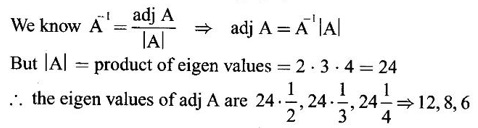
 has an eigen vector
has an eigen vector 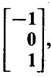 find the corresponding eigen value of A.
find the corresponding eigen value of A.![]() is an eigen vector.
is an eigen vector.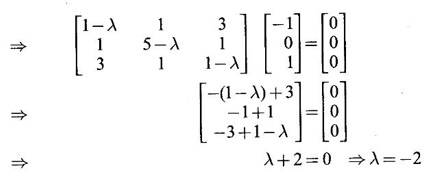
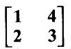
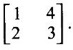
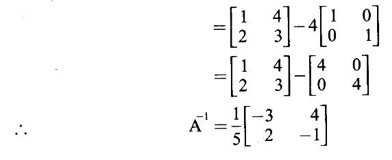
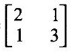
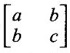
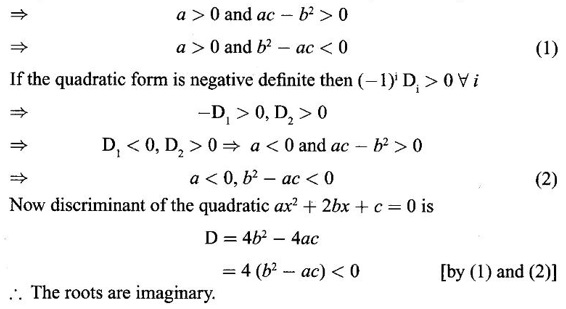
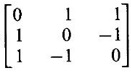
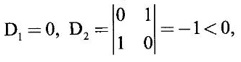
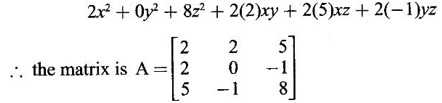
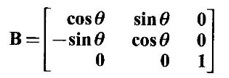
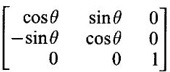

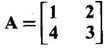
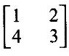
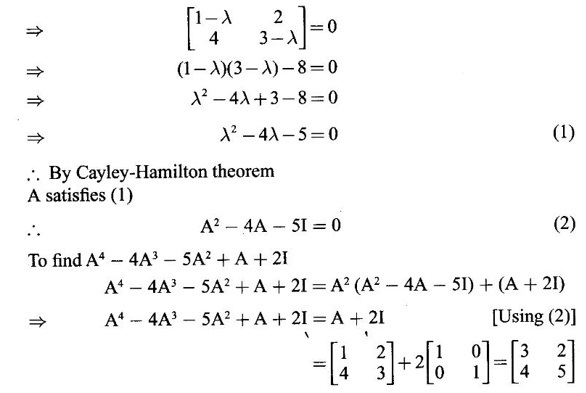
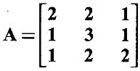
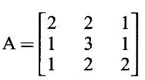
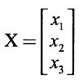 be the eigen vector corresponding to the eigen value 1.
be the eigen vector corresponding to the eigen value 1.
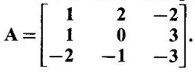
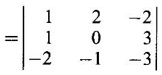
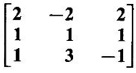 find the other eigen values.
find the other eigen values.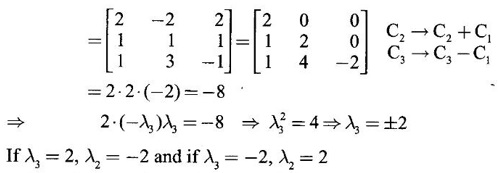
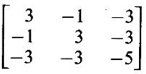
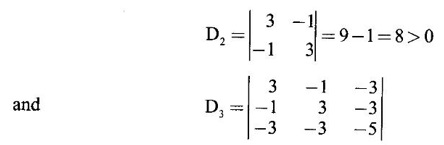
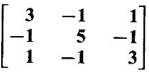 are 3 and 6. Find the eigen values of A-1.
are 3 and 6. Find the eigen values of A-1.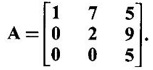

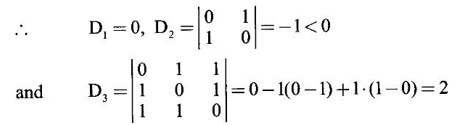
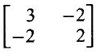
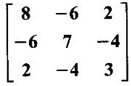 are 3 and 0. What is the third eigen values?
are 3 and 0. What is the third eigen values?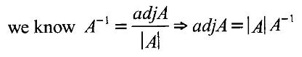
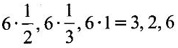
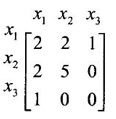
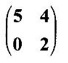
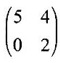
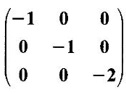
 is a lower triangular matrix,
is a lower triangular matrix,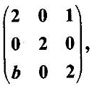 then find the value of b.
then find the value of b. 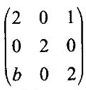 and let λ1, λ2, λ3 be the eigen values of A.
and let λ1, λ2, λ3 be the eigen values of A.
Matrices and Calculus: Unit I: Matrices : Tag: : Solved Example Problems | Matrices - Questions and Answers
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
