Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Properties of Ideal Gas
An imaginary gas which obeys the equation of state as pV = mRT at all pressures and temperatures is known as ideal gas.
PROPERTIES OF IDEAL GAS An imaginary gas which obeys the equation of state as pV = mRT at all pressures and temperatures is known as ideal gas. If the pressure of real gas tends to zero or temperature tends to infinity, the real gas behaves as an ideal gas. In equation of state, the volume may remain constant or pressure may remain constant. But, the minimum possible temperature is zero Kelvin. So, it is equal to -273.15°C. Therefore, this temperature is called absolute temperature. Ideal gases obey the law of equation of state (pV = mRT) and have the constant specific heats. But these two conditions are opposite for real gases. It means, the real gases do not obey the law of equation of state and its specific heat values change with temperature either linear or non-linear. By first law of thermodynamics, Heat = Work + Change in internal energy Q = W + ΔU Again, it is rearranged into Tds = du + pdv There are two assumptions made: 1. Both internal energy and entropy are the function of temperature and volume. 2. Both internal energy and entropy are the function of temperature and pressure. Case 1: Both internal energy and entropy as the function of temperature and volume The internal energy is assumed as a function of temperature and volume. So, it can be written as u = f(T, v) By mathematic rule, Now, the entropy is assumed as a function of temperature and volume. So, it can be written as s = f(T, v) By mathematical rule, Similarly, the coefficients of dv are compared in equation (5.3) and (5.4), Differentiating the equation (5.5) with respect to v by keeping T as constant, Similarly, the equation (5.6) is differentiated with respect to T by keeping v as constant. Equating the equations (5.10) and (5.12), Therefore, it indicates that the internal energy does not vary with volume at constant temperature. Therefore, this internal energy equation is applicable for an ideal gas for any process. Case 2: Both internal energy and entropy as the function of temperature and pressure The internal energy is assumed as a function of temperature and pressure. So, it can be written as u = f(T, p) By mathematical rule, Substituting the value of du in equation (5.1), From ideal gas equation, pv = RT v = RT/P Differentiating above equation with respect to p, Substituting dv in equation (5.14), Now, the entropy is assumed as a function of temperature and pressure. So, it can be written as s = f(T, p) By mathematical rule, Differentiating the equation (5.16) with respect to pressure (p) by keeping temperature (T) as constant, Similarly, differentiating the equation (5.17) with respect to temperature by keeping pressure (p) as constant, But the equation of state is given by pv = RT ... (5.21) Differentiating the equation (5.21) with respect to 'T' by keeping pressure as constant. Multiplying by T on both sides of the equation (5.20), it can be written as We know that Enthalpy = Internal energy + Flow energy. h = u + pv = u + RT (⸪ pv = RT) Differentiating the above equation, Then dh = du + RdT From first law of thermodynamics, Q = W + ΔU Q = ΔU + W From equation (5.24), Tds = du + pdv = dh - d(pv) + pdv (⸪ u = h - pv) = dh – vdp – pdv + pdv (⸪ By differentiation multiplication rule) Tds = dh - vdp Integrating on both sides, We know that R = Cp - Cv Then equation (5.26) becomes We know that Among three equations (5.25), (5.26) and (5.27), any one may be used to find the entropy change of any process depending on the available properties.1. Specific Heats of Ideal Gas

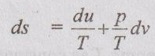

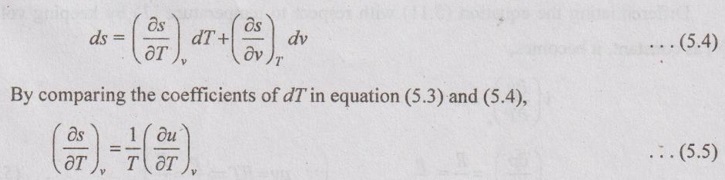





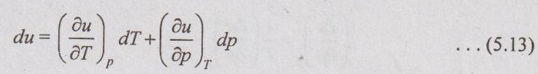


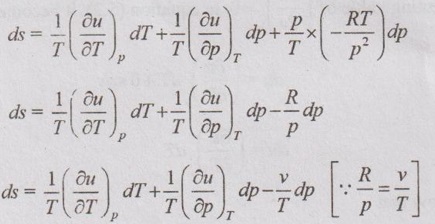
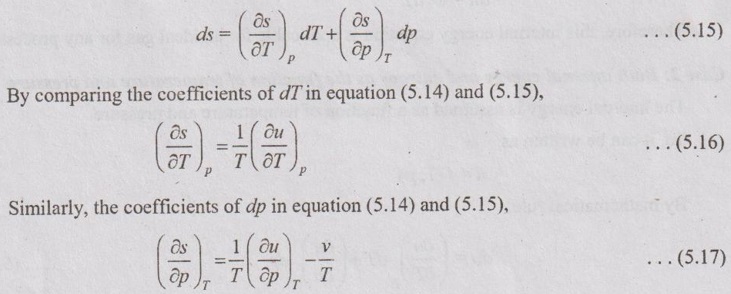

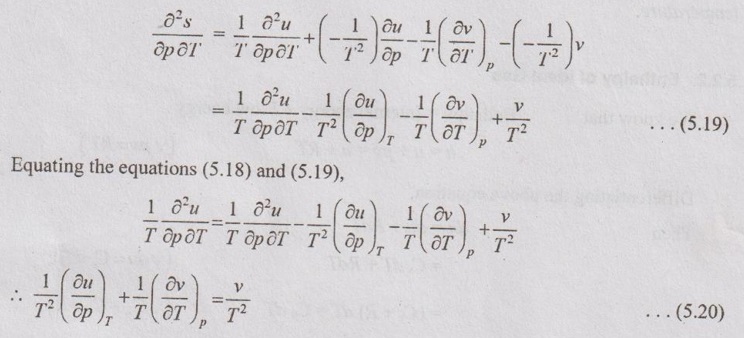

 Hence, it indicates that the internal energy does not change with pressure at constant temperature.
Hence, it indicates that the internal energy does not change with pressure at constant temperature.2. Enthalpy of Ideal Gas

3. Entropy of Ideal Gas

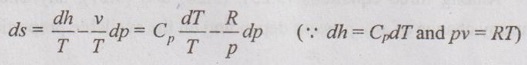
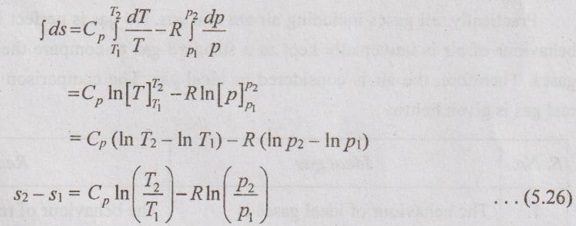
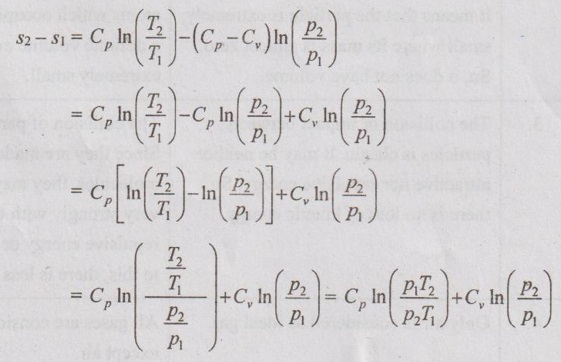
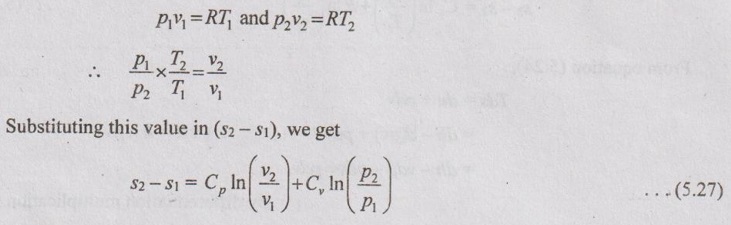
Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : - Properties of Ideal Gas
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
