Matrices and Calculus: Unit I: Matrices
Properties of eigen values
Matrices
A square matrix A and its transpose AT have the same eigen values.
Properties of eigen values 1. A square matrix A and its transpose AT have the same eigen values. Proof Eigen values of A are the roots of its characteristic equation This shows that the characteristic polynomial of A and AT are the same. Hence the characteristic equations of A and AT is (1). ⸫ A and AT have the same eigen values. 2. Sum of the eigen values of a square matrix A is equal to the sum of the elements on its main diagonal. Proof Let A be a square matrix of order n. Note Sum of the diagonal elements of A is called the trace of A. ⸫ Sum of the eigen values = trace of A 3. Product of the eigen values of a square matrix A is equal to │A│. Proof Let A be a square matrix of order n. Then its characteristic equation is | A-λI | = 0 If λ1, λ2,...., λn are the n roots of (1), then from theory of equations, Note If at least one eigen value is 0, then |A|= 0 ⸫ A is a singular matrix. If all the eigen values are non-zero, then |A| ≠ 0 ⸫ A is a non-singular if all the eigen values are non-zero. 4. If λ1, λ2,...., λn are non-zero eigen values of square matrix of order n, then Proof Let λ be any non-zero eigen value of A, then there exists a non-zero column matrix X such that AX = λX. Since all the eigen values are non-zero, A is non-singular. So 1/λ is an eigen value of A-1. This is true for all the eigen values of A. ⸫ 1/λ1, 1/λ2, …, 1/λn are the eigen values of A-1. Note that the eigen vector for A corresponding to 1/λ is also X. 5. If λ1, λ2,...., λn are the eigen values of A, then (i) cλ1, cλ2,...., cλn are the eigen values of cA, where c ≠ 0 (ii) λ1m, λ2m,...., λnm are the eigen values of Am, where m is a positive integer. Proof Let λ be any eigen value of A, then there exists a non-zero column matrix X such that AX = λ X (i) Multiply by c ≠ 0 then c(AX) = c(λX) ⇒ (cA) X = (cλ) X ⸫ cλ is an eigen value of cA. This is true for all eigen values of A. ⸫ c λ1, c λ2, ..., c λn are the eigen values of cA. (ii) Now A2X = A(AX) = A(λ X) [using (1)] = λ (AX) = λ (λ X) ⸫ A2X = λ2 X ⇒ λ2 is an eigen value of A2. Similarly A3X = A(A2X) = A(λ2X) = λ2 (AX) = λ2 (λX) A3X = λ3X ⇒ λ3 is an eigen value of A3. Proceeding in this way, we have AmX = λmX for any positive integer m. This is true for all eigen values. ⸫ λ1m, λ2m,...., λnm are eigen values of Am. 6. If λ1, λ2,...., λn are the eigen values of A, then (i) λ1 – k, λ2 – k,..., λn – k are the eigen values of A - KI. (ii) α0 λ12 + α1λ1 + α2, α0 λ22 + α1λ2 + α2,..., ‚ α0 λn2 + α1λn + α2 are the eigen values of α0A2 + α1A + α2I. Proof Let λ be any eigen value of A then AX = λ X (1) where X ≠ 0 is a column matrix. ⸫ AX - KX = λ X - KX ⇒ (A – KI)X = (λ – K)X ⸫ λ - K is an eigen value of A – KI. This is true for all eigen values of A. ⸫ λ1 — K, λ2 — K,..., λn -K are the eigen values of A – KI. (ii) We have AX = λ X and A2X = λ2X. ⸫ α0 (A2X) = α0 (λ2X) and α1 (AX) = α1(λX) ⸫ α0 (A2X) + α1 (AX) = α0 (λ2X) + α1(λX) Adding α2X on both sides, we get α0 (A2X) + α1 (AX) + α2X = α0 (λ2X) + α1 ( λ X) + α2X ⇒ (α0 A2 + α1A + α2I)X = (α0λ2 + α1λ + α2)X This means α0λ2 + α1λ + α2 is an eigen value of a α0 A2 + α1A + α2I. This is true for all eigen values of A. ⸫ α0 λ12 + α1λ1 + α2, α0 λ22 + α1λ2 + α2,..., ‚ α0 λn2 + α1λn + α2 are the eigen values of α0 A2 + α1A + α2I. Note 1. The eigen values of the unit matrix 2. The eigen values of a triangular matrix 3. If λ is an eigen value of A then AX = λX. We have seen A2X = λ2X, ..., AmX = λmX. Thus the eigen values of A, A2, …, Am are λ, λ2, ..., λm which are all different. But they all have the same eigen vector X. Similarly, λ and α0 λ2 + α1λ + α2 are eigen values of A and α0 A2 + α1A + α2I. But they have the same eigen vector X. WORKED
EXAMPLES Example 14 Find the sum and product of the eigen values of the matrix Solution Sum of the eigen values = Sum of the elements on the main diagonal = 1 + 0 + (-3) = −2 Product of the eigen values = |A| = = 1(0 + 3) − 2 (−3 + 6) − 2(−1 – 0) = 3 – 6 + 2 = −1 Example 15 If 2 and 3 are eigen values of A = Solution Given 2 and 3 are two eigen values of A. Let λ be the 3rd eigen value. We know, sum of the eigen values = sum of the diagonal elements. ⇒ 2 + 3 + λ = 3 + (−3) + 7 ⇒ λ = 2 So, eigen values of A are 2, 2, 3 ⸫ Eigen values of A-1 are 1/2, 1/2, 1/3 and eigen values of A3 are 23, 23, 33 ⇒ 8, 8, 27. Example 16 If Solution Example 17 If A = Solution Expanding by C1, (3 - λ) (2 - λ) (5 - λ) = 0 ⇒ λ = 3, 2, 5 are the eigen values of A. ⸫ the eigen values of A2 - 2A + I are 32 – 2 ⸱ 3 + 1, 22 - 2 ⸱ 2 + 1, 52 - 2.5 + 1 i.e., the eigen values of A2 - 2A + I are 4, 1, 16. Example 18 The product of two eigen values of the matrix A = Solution Let λ1, λ2, λ3 be the eigen values of A. Given λ1 ⸱ λ2 = 16 We know that λ1⸱ λ2⸱ λ3 = |A| = 6(9 − 1) + 2(−6 + 2) + 2(2 − 6) ⇒ 16 λ3 = 48 – 8 – 8 - 32 ⇒ λ3 = 2 Example 19 Find the eigen values of the matrix Solution Let A = The characteristic equation of A is |A — λI| = 0 Example 20 If α, β are the eigen values of Solution Let A = EXERCISE 1.1 Find eigen values and eigen vectors of the following
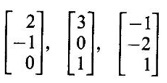
matrices. ANSWERS TO EXERCISE 1.1 1. λ = 1, 3, -4; eigen vectors 2. λ = 0, −1, 2; eigen vectors 3. λ= -3, -3, 5; eigen vectors 4. λ = 3, 6, 9; eigen vectors 5. λ = 2, 2, 8; eigen vectors 6. λ = −2, 3, 6; eigen vectors 7. λ = 1, 1, 4; eigen vectors


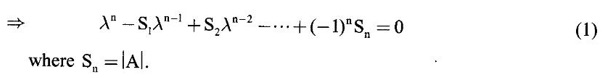

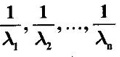 are eigen values of A-1.
are eigen values of A-1.
 are 1, 1, 1 and the corresponding eigen vectors are
are 1, 1, 1 and the corresponding eigen vectors are 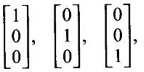 which are independent.
which are independent.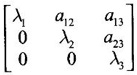 are the main diagonal elements λ1, λ2,λ3
are the main diagonal elements λ1, λ2,λ3
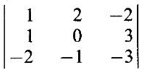
 find the eigen values of A-1 and A3.
find the eigen values of A-1 and A3.![]() is an eigen vector of the matrix
is an eigen vector of the matrix 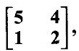 find the corresponding eigen value.
find the corresponding eigen value.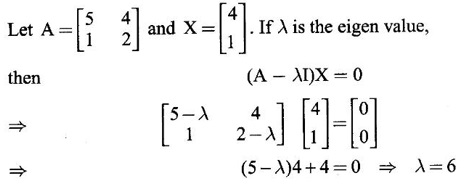
 find the eigen values of A2 - 2A + I .
find the eigen values of A2 - 2A + I .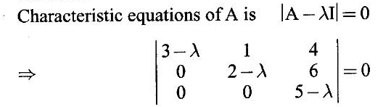
 is 16. Find the third eigen value.
is 16. Find the third eigen value.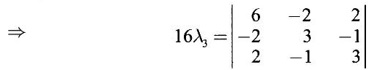
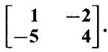 Hence find the matrix whose eigen values are 1/6 and −1.
Hence find the matrix whose eigen values are 1/6 and −1.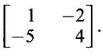

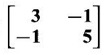 form the matrix whose eigen values are α3, β3.
form the matrix whose eigen values are α3, β3.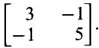 Since α, β are the eigen values of A, by property 5(ii), α3, β3 are eigen values of A3.
Since α, β are the eigen values of A, by property 5(ii), α3, β3 are eigen values of A3.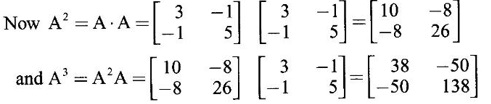

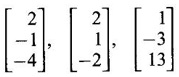
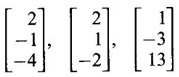
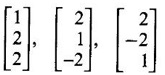
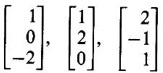

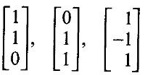
Matrices and Calculus: Unit I: Matrices : Tag: : Matrices - Properties of eigen values
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
