Theory of Machines: Unit II: Gears and Gear Trains
Problems for practice
Gears and Gear Trains - Theory of Machines
Problems for practice: Gears and Gear Trains - Theory of Machines
PROBLEMS FOR PRACTICE 1. Arrange a compound gear train for reducing a speed in two stages from 2400 to 200 rpm in the same direction. The wheels available range from one of 20 teeth to that of 120 teeth rising by steps of 5. There is only one wheel having a particular number of teeth. Give the sketch of gear train. [Ans. Drivers 20 and 30 teeth; Followers 80 and 90 teeth] 2. In a compound train of wheels spur wheel 1, with 40 teeth and rotating at 15 rpm drives a pinion 6 with pinion 15 teeth at 300 rpm across two intermediate spindles. The first intermediate spindle has wheels 2 and 3 and the second carries wheels 4 and 5. Wheel 2 gearing with wheel 1 while 3 gearing with wheel 4 and 5 gearing with wheel 6. If wheels 2, 4 and 5 have 20, 15 and 30 teeth respectively, calculate the number of teeth on wheel 3. [Ans. 75] 3. An arm carries three wheels whose centres lie on a straight line. The first wheel has 40 teeth, the second 50 and the third 60. If the arm rotates once about the centre of the first wheel which is fixed, find the fumber of revolutions of the last wheel. If instead of being fixed, the first wheel makes 10 revolutions in a direction opposite to the arm while the later makes one revolution, find the number of revolutions of the last wheel. [Ans. 0.333 rpm; 6.333 rpm] 4. In a reverted epicyclic gear train, the arm A carries two gears B and C and a compound gear D-E. The gear B meshes with gear E and the gear C meshes with gear D. The number of teeth on gears B, C and D are 75, 30 and 90 respectively. Find the speed and direction of gear C when gear B is fixed and the arm A makes 100 rpm clockwise. [Ans. 400 rpm CCW] 5. In a reverted epicyclic gear train, the arm F carries two wheels A and D and a compound wheel B-C. The wheel A meshes with wheel B and the wheel D meshes with wheel C. The number of teeth on wheels A, D and C are 80, 48 and 72 respectively. Find the speed and direction of wheel D and wheel A is fixed and arm F makes 200 rpm clockwise. [Ans. 400 rpm (CW)] 6. In an epicyclic gear train, an arm carries two gears A and B are having 42 and 58 teeth respectively. If the arm rotates at 215 rpm in the anticlockwise direction about the centre of the gear A which is fixed, determine the speed of gear B. If the gear A instead of being fixed, makes 365 rpm in the clockwise direction, what will be the speed of gear B. [Ans. 371 rpm (CCW); 635 rpm (CCW)] 7. An epicyclic gear consists of a pinion, a wheel of 40 teeth and an annulus with 84 internal teeth concentric with the wheel. The pinion gears with the wheel and the annulus. The arm that carries the axis of the pinion rotates at 100 rpm. If the annulus is fixed, find the speed of the wheel. If wheel is fixed, find the speed of the annulus. [Ans. 310 rpm; 147.6 rpm] 8. In an epicyclic gear train of the 'sun and planet type', the pitch circle diameter of the internally toothed ring gear is to be around 216 mm as nearly as possible. The module is 4 mm. When the ring gear is stationary, the arm which carries three planet wheels of equal size is to make one revolution for every five revolutions of the driving spindle carrying the sun gear. (i) Determine suitable number of teeth for all the gears. (ii) Find the exact diameter of pitch circle of the ring gear. (iii) If a torque of 20 N.m is applied to the spindle carrying the sun gear, what torque will be required to keep the ring gear stationary? [ Ans. ns. TB 14; TC = 21; TD = 56; 224 mm; T = 80 N.m] Fig.5.25 shows diagrammatically a compound epicyclic gear train. Wheels A, D and E are free to rotate independently on spindle O, while B and C are compound and rotate together on spindle P, on the end of arm OP. All the teeth on different wheels have the same module. A has 12 teeth, B has 30 teeth and C has 14 teeth cut externally. Find the number of teeth on wheels D and E which are cut internally. If the wheel A is driven clockwise as 1 rps., while D is driven counter clockwise at 5 rps, determine the magnitude and direction of the angular velocities of arm OP and wheel E. 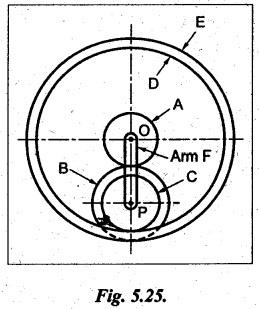
Theory of Machines: Unit II: Gears and Gear Trains : Tag: : Gears and Gear Trains - Theory of Machines - Problems for practice
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
