Engineering Mechanics: Unit V: Dynamics of Particles
Position, Velocity and Acceleration in Curvilinear Motion
For a particle moving along a curved path in a plane, the position, velocity and acceleration are vector quantities.
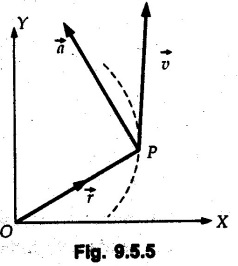
Position, Velocity and Acceleration in Curvilinear Motion • For a particle moving along a curved path in a plane, the position, velocity and acceleration are vector quantities. • Consider a particle moving along a curved path as shown in Fig. 9.5.1. If the particle is at point 'P' at time 't', then its position is defined by vector • Let the particle be at position P' at time t + Δt. The position vector at P' is • The distance travelled Δs is the length of arc PP'. will be the average velocity and the instantaneous velocity is • The magnitude of As Δt → 0, P' is very close to P and the direction of • Hence velocity of the particle is always tangential. • Consider velocity vectors at two points A and B as shown in Fig. 9.5.3. They are redrawn from a common point as shown in Fig. 9.5.4. • The change in velocity is • The average acceleration is and instantaneous acceleration is • The three vectors are shown in Fig. 9.5.5. Note that the O velocity is tangential whereas acceleration is not.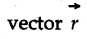 which is directed from O to P.
which is directed from O to P.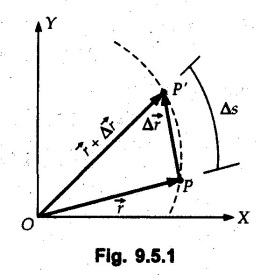
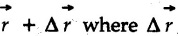 is the change in position i.e. displacement of the particle represented by the vector
is the change in position i.e. displacement of the particle represented by the vector ![]()

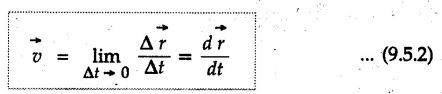
![]() is called speed.
is called speed.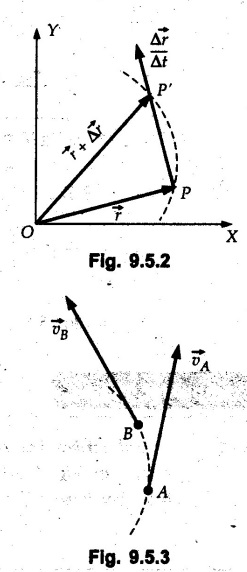
![]() is tangential to the curve.
is tangential to the curve.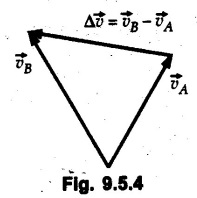
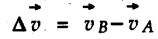
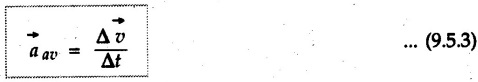
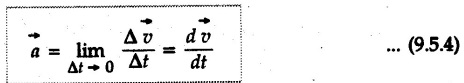
Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : - Position, Velocity and Acceleration in Curvilinear Motion
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
