Engineering Physics: Unit III: a. Oscillations
Plane Progressive Waves or Traveling Waves
Progressive wave originating from a point source and propagating through an isotropic medium travel with equal velocity in all directions.
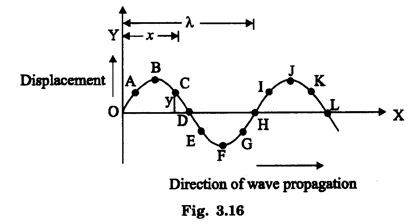
PLANE PROGRESSIVE WAVES OR TRAVELING WAVES Progressive wave originating from a point source and propagating through an isotropic medium travel with equal velocity in all directions. At any instant, the wavefront (locus of all particles vibrating with the same phase) will be spherical in nature. If the sphere of very large radius is considered, the spherical wave will approximate to a plane surface and the waves are called plane progressive waves. By definition, the distance travelled by the wave in one time-period (T) of vibration of particle = wave length (λ) ie Distance travelled in T second = λ ⸫ Distance travelled in one second = λ/T But, distance travelled in one second = wave speed v. substituting value of T from the relation between frequency (n) and time period T v = n λ This relation holds for all types of waves. On propagation of wave in a medium, the particles of medium execute simple harmonic motion. If a plane progressive wave is propagating in a medium along positive X - axis. (i.e. from left to right) (Fig. 3.16) then the positions of particles O, A, B, C, D ... are shown. As the wave propagates, all the particles of the medium begin to vibrate to and fro about their mean positions. In fig. 3.16 the instantaneous positions of these particles are shown. The curve joining these positions represents the progressive wave. Let the particle begin to vibrate from origin O at time t = 0. If y is the displacement of the particle at time t, then equation of particle executing simple harmonic motion about O is where A is amplitude and ω is angular velocity. If n is frequency of wave, then ω = 2 πn. As the advancing wave reaches the other particles A, B, C... (beyond particle at O), these particles begin to vibrate. If v is the speed of wave and C is a particle at a distance x from O, then the time taken by wave to reach point C is x/v seconds therefore the particle will start vibrating x/v seconds after particle at O. Therefore, the displacement of particle C at any time t will be the same which was of particle O at time The displacement of particle O at time Thus the displacement of particle C at a distance x from origin O at any time t is given by If T is time-period and λ the wavelength of wave, then This equation is expressed as The equation (2) is also expressed as Any of the equations (2), (3), (4), (5), represents the equation of a plane progressive wave propagating along positive direction of X - axis. Out of these, the equation (5) is often used. If the wave is propagating along negative X - axis, then the equation of plane progressive wave may be obtained by substituting - x for x, so that equation (5) takes the form If ϕ is the phase difference between this wave travelling along positive X - axis and another wave, then the equation of the wave may be expressed as This is the most general equation of a plane progressive wave travelling along positive direction of X-axis. This is particle acceleration. Comparing (11) and (12) This is the differential equation of wave motion. It can be shown that in case of progressive waves, if, t is increased by δt and x by v δt Thus, in a time δt, the wave advances through v δt. Hence, v is the velocity of the wave. 1. Each particle of the medium executes vibration about its mean position. The disturbance progresses onward from one particle to another. 2. The particles of the medium vibrate with same amplitude about their mean positions. 3. Each successive particle of the medium performs a motion similar to that of its predecessor along the propagation of the wave, but later in time. 4. The phase of every particle changes from 0 to 2π. 5. No particle remains permanently at rest. Twice during each vibration, the particles are momentarily at rest at extreme positions, different particles attain the position at different time. 6. Transverse progressive waves are characterised by crests and troughs. Longitudinal waves are characterised by compressions and rarefactions. 7. There is a transfer of energy across the medium in the direction of propagation of progressive wave. 8. All the particles have the same maximum velocity when they pass through the mean position. 9. The displacement, velocity and acceleration of the particle separated by mλ are the same, where m is an integer.Relation between Frequency, Wave - Speed and Wavelength
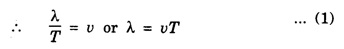
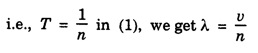
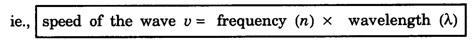
Wave Equation of a Plane - Progressive Wave

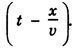
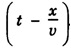 can be obtained by substituting
can be obtained by substituting 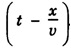 in place of t in equation (1).
in place of t in equation (1).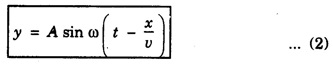
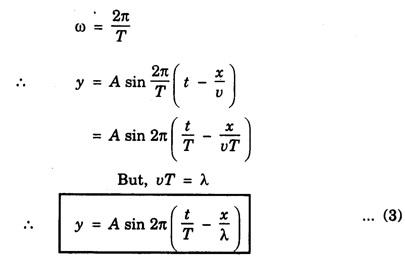
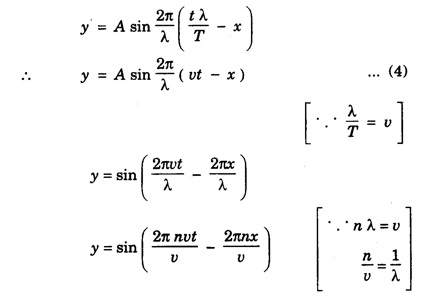
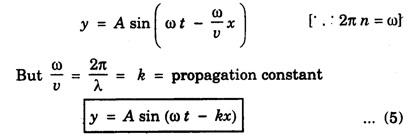
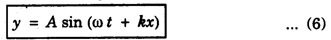
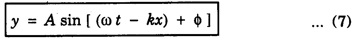
Differential equation of wave motion
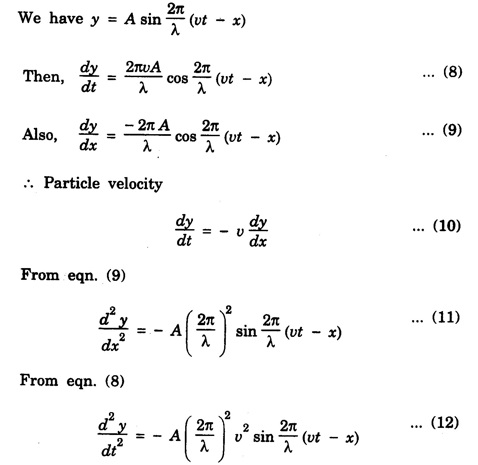
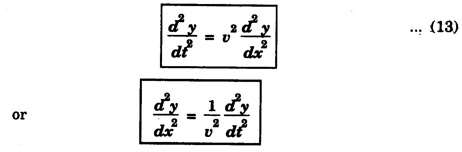
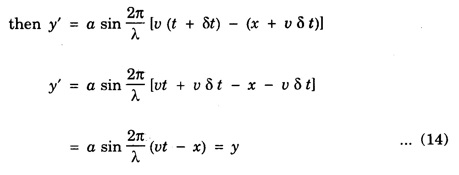
Characteristics of progressive wave
Engineering Physics: Unit III: a. Oscillations : Tag: : - Plane Progressive Waves or Traveling Waves
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
