Engineering Physics: Unit IV: Basic Quantum Mechanics
Particle in a Rectangular Three - Dimensional Infinite Well
Quantum Mechanics
Let a particle of mass m be in motion in a rectangular deep potential (Fig. 6.14) with sides of lengths a, b, c, parallel to the x,y and z-axes respectively.
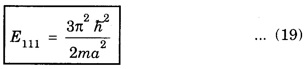
PARTICLE IN A RECTANGULAR THREE - DIMENSIONAL INFINITE WELL Let a particle of mass m be in motion in a rectangular deep potential (Fig. 6.14) with sides of lengths a, b, c, parallel to the x,y and z-axes respectively. If there is no force acting on the particle inside the box, so that in the region. 0 < x < a 0 < y < b 0 < 2 < c the potential energy V(x, y, z) = 0 and outside the box V (x, y, z) = ∝ For the motion of the particle inside the box, the Schrodinger time - independent wave equation is: It is assumed that the wave-function Ψ (x, y, z) is equal to the product of three functions X, Y, and Z each of which is a function of one variable only. Thus we have Substituting eqn (3) in eqn. (2), we have, Note: We used ordinary derivatives instead of partial derivatives because each of the functions X, Y and Z is a function of one variable only. Dividing eqn. (4) by XYZ, we get In this equation Since the velocity of the particle, being a vector quantity, can be resolved into three components along the coordinate axes, the kinetic energy E is expressed as the sum of the corresponding terms Ex, Ey and Ez. Hence, Therefore, from equations (5) and (6), we get This equation gives three independent equations: The eqn. (7) is the equation for the one-dimensional case. The boundary condition applicable to the solution is: X (0) = X (a) = 0 So the eigen values of Ex are given by where nx = 1, 2, 3, ...... and the corresponding normalized eigen functions are given by: The solution for Y and Z are of the same form, therefore, we have: Substituting the expressions for Ex, Ey and Ez in eqn. (6), we have: where nx = 1, 2, 3, …….. ny = 1, 2, 3, …….. nz = 1, 2, 3, …….. This equation gives the eigen values of the energy of the particle. These values are called the energy-levels of the particle. The total normalized wave-function inside the box for the stationary states is given by: where nx, ny and nz are integers. The wave-function is zero outside the box. It is easily proved that the wave-function is normalized, because: From Eqs. (16) and (17) we get the following conclusions: 1. Three integers nx, ny and nz, which are called quantum numbers, are required to describe each stationary state. If we change the sign of the quantum numbers, there is no change in the energy and in the wave-function except that the minus will appear on the right hand side of Eq. (17). Therefore, all the stationary states are given by the positive integral values of nx, ny and nz. No quantum number can be zero, because if any one of them is taken zero, then Ψ (x, y, z) = 0, which would mean that the particle does not exist in the box. 2. The lowest possible energy, i.e., the energy in the ground state, occurs when nx = ny = nz = 1 and it depends on the values of a, b and c. 3. If the particle is confined in a cubical box in which a = b = c = a, the eigen-values of energy are given by: In this case energy of the particle in the ground state is given by: No other state will have this energy, and this state has only one wave-function. Therefore, the ground state and the energy-level are said to be non-degenerate. 4. In a cubical box, the energy depends on the sum of the squares of the quantum numbers. Consequently the particle having the same energy in an excited state will have several different stationary states, or different wave-functions. Such states and energy-levels are said to be degenerate.
Wave Equation of the Particle
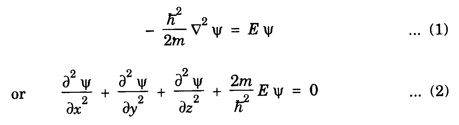
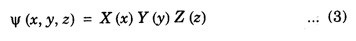
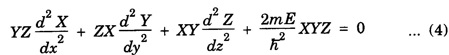

![]() is a constant for a particular value of the kinetic energy.
is a constant for a particular value of the kinetic energy.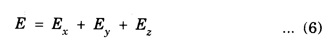
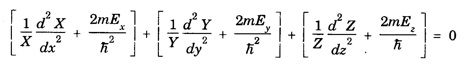
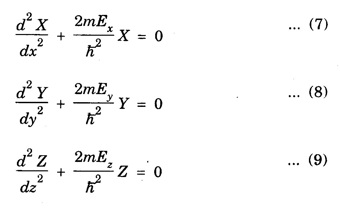
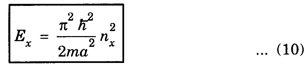
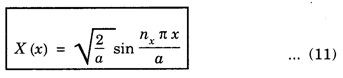
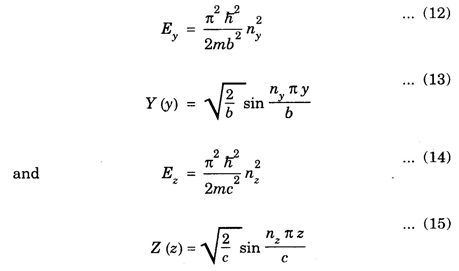
Eigen Values of Energy

Wave function
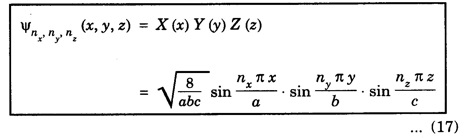
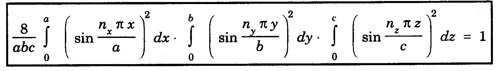
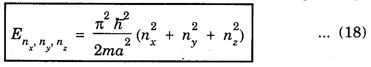
Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Quantum Mechanics - Particle in a Rectangular Three - Dimensional Infinite Well
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
