Engineering Physics: Unit IV: Basic Quantum Mechanics
Particle in a Infinite Potential (One - Dimensional Box)
Quantum Mechanics
Consider a particle of mass m moving between two rigid walls of a box or infinite deep potential well at x = 0 and x = a along x-axis.
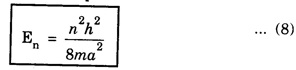
PARTICLE IN A INFINITE POTENTIAL (One - Dimensional Box) Consider a particle of mass m moving between two rigid walls of a box or infinite deep potential well at x = 0 and x = a along x-axis. This particle is bouncing back and forth between the walls of the infinite well. The potential energy (V) of the particle inside the box is constant. It is taken as zero for simplicity (Fig. 6.9). The walls are infinitely high. The potential energy V of the particle is infinite outside the walls. Thus, the potential function is given by This potential function is known as square well potential. (Fig. 6.9) • The particle cannot come out of the box well. Also, it can not exist on the walls of the box. So, its wave function Ψ is 0 for x ≤ 0 and x ≥ a. Now, task is to find the value Ψ within the box i.e., between x = 0 and x = a. Schroedinger's wave equation in one-dimension is given by Since V = 0 between the walls, eqn (1) reduces to The general solution of eqn (3) is given by Here, A and B are two unknown constants. The values of the constants A and B are determined by applying the boundary conditions. Boundary condition (i) Ψ = 0 at x = 0 Applying this condition to eqn (4), we have Boundary condition (ii) Ψ = 0 at x = a Applying this condition to eqn (4), we have 0 = A sin ka + 0 [⸪ B = 0] A sin ka = 0 It is found that either A = 0 or sin ka = 0 A cannot be '0' since already one of the constants B is '0'. If A is also 0, then the wave function is zero even in between walls of the box. Hence, A should not be zero. ⸫ sin ka = 0 sin ka is '0' only when ka takes the value of nπ ie., ka = nπ where n is positive integer 1, 2, 3 ... On squaring eqn (5), we have Equating eqn (6) and eqn (7), we have Energy of the particle substituting eqn (5) in eqn (4), we have Here n = 1, 2, 3 ... For each value of n, there is an energy level. The particle in a box cannot possess any arbitrary amount of energy. It can only have discrete energy values specified by eqn (8). In otherwords, its energy is quantised. Each value of En is known as eigen value and the corresponding Ψn is called as eigen function.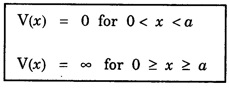


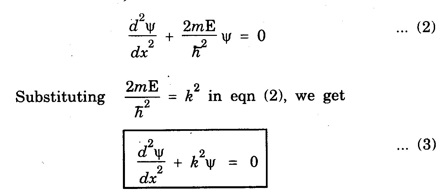
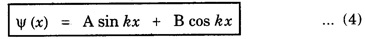
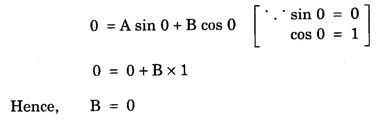



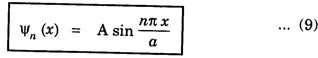
Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Quantum Mechanics - Particle in a Infinite Potential (One - Dimensional Box)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
