Particle in a Finite Potential Wells (Qualitative)

PARTICLE IN A FINITE POTENTIAL WELLS (Qualitative)

• Consider a particle of mass m moving with velocity v along the x-direction between x = 0 and x = a.

• The walls of the box are not rigid. Hence it is represented by a potential well of finite depth.

Step I: Let E be the total energy of particle inside the box and V be its P.E. The potential energy which is assumed to be zero within the box and its value outside the box is finite say V0 and V0 > E.

The variation of potential with x is shown in fig. 7.17.

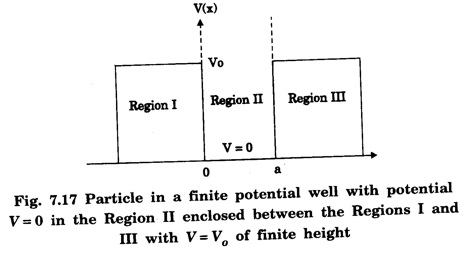
V(x) = V0 x ≤ 0 Region I 

V(x) = 0 0 < x < a Region II 

and V(x) = V0 x ≥ a Region III

Classically, the particle with energy E < V0 cannot be present in regions I and III outside the box.

Consider the quantum mechanical picture of the particle in one dimension. If Ψ is the wave function associated with the particle then Schrodinger's time independent equation for it is,

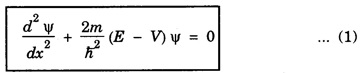
Step II: Consider the three regions I, II, III separately and let ΨI, ΨII, ΨIII be the wave functions in them respectively.

We have for region I.

For region II,

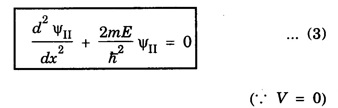
and for region III,

Then the equation in the three regions is written as,

Step III: The solutions of these equations are of the form.

Step IV: As x → ±∞, Ψ should not become infinite. Hence B = 0 and C = 0.

Hence the wave functions in three regions are

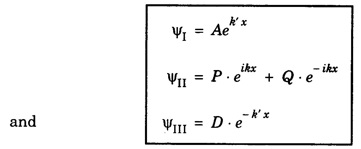
Step V: The constants A, P, Q and D can be determined by applying the boundary conditions. The wave function Ψ and its derivative d Ψ/ dx should be continuous in the region where Ψ is defined.

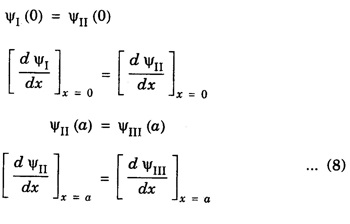
• Using these four conditions, we get four equations from which the four constants A, P, Q, D can be determined. Thus the wave functions can be known completely. 

• The first three wave functions and probability densities when plotted against x are as shown in fig. 7.18.

• The eigen functions are similar in appearance to those of infinite well except that they extend a little outside the box.

• Even though the particle energy E is less than the P.E. V0, there is a definite probability that the particle is found outside the box.

• The particle energy is not enough to break through the walls of the box but it can penetrate the walls and leak out.

• This shows penetration of the particle into the classically forbidden region.

• The energy levels of the particle are still discrete but there are a finite number of them. Such a limit exists because, soon the particle energy becomes equal to V0.

For energies higher than this the particle energy is not quantised but may have any value above V0.

• These predictions are unique in quantum mechanics and shows different behaviour from that expected in classical physics.

Band theory of solids (Zone theory)

The free electron theory explains the properties like thermal conductivity, electrical conductivity and specific heat of most of the metals.

But, it fails to explain why some solids are conductors, some are insulators and others are semiconductors.

A solution to this problem was given by band theory of solids and is called zone theory.

According to free electron theory, the potential energy of the electron inside the crystal through which an electron moves is supposed to be constant (zero). So it is completely free to move about in the crystal, restrained only by the surface of the crystal.

Postulates 

1. According to band theory, potential energy of electron within the crystal is periodic due to periodicity of the crystal i.e., free electrons move inside periodic lattice field.

2. The potential energy of the solid varies periodically with the periodicity of space lattice ‘a’ which is nothing but interatomic spacing.

Inside a real crystal, the electrons (-ve charge) move through periodic arrangement of positively charged holes (+ve charge) as shown in the fig. 7.19(a)

Fig. 7.19(b) shows one dimensional periodic potential distribution for a crystal. It is assumed that the potential energy of the electron at the positive ion site is zero and it is maximum when it is half way between the adjacent nuclei.