Matrices and Calculus: Unit III: Functions of Several Variables
Partial Derivatives
Definition, Theorem, Worked Examples, Exercise with Answers
Functions of two or more independent variables appear in many practical problems more often than functions of one independent variable.
PARTIAL DERIVATIVES Functions of two or more independent variables appear in many practical problems more often than functions of one independent variable. The concept of derivative of a single variable function f(x) is extended to functions of two or more variables. Suppose f(x, y) is a function of two independent variables x and y, we treat y as constant and find the derivative of f(x, y) w.r.to x, then the derivative is called a partial derivative. Partial derivatives find applications in a wide variety of fields like fluid dynamics, electricity, physical sciences, econometrics, probability theory etc. Definition 3.2.1 Let z = f(x, y) be a real function of two independent variables x and y. Let (x0, y0) be a point in the domain of f. The partial derivative of f(x, y) w.r.to x at (x0, y0) is the limit. Similarly, partial derivative of f(x, y) w.r.to y at (x0, y0) is the limit If the partial derivatives of z = f(x, y) exist at any point in its domain, then the partial derivatives w.r.to x is simply written as as Similarly, the partial derivative w.r.to y is written as 1. Geometrical meaning of Let z = f(x, y) be a real function of two independent variables x, y. For every point (x, y) in its domain R in the xy plane there is a real number z, where f(x, y) = z. The set of all points (x, y, z), where z = f(x, y), in space determine a surface S. This surface is called the graph of the function f. Thus z = f(x, y) represents a surface in space. The equation y = y0 represents a vertical plane (parallel to xoz plane) intersecting the surface in a curve C : z = f(x, y0). The partial derivative Similarly, the partial derivative Note (1) If z = f(x, y) then f(x, y) = k for all points in the domain of f, where k is a constant, is called a level curve of function f. (2) If u = f(x, y, z) be a function of three independent variables x, y, z then the graph of ƒ is a 4-dimensional surface. f(x, y, z) = c, where c is a constant, is called a level surface. For different c, we have different level surfaces. 2. Partial derivatives of higher order Let z = f(x, y) be a function of 2 independent variables. The derivatives It can be shown that if fx, fy, and fxy, are continuous then fxy = fyx. In fact the elementary functions that we come across satisfy these conditions. In many practical applications also these conditions are satisfied. So, we shall assume this in our discussions. Differentiating the second order derivatives partially w.r.to x, y we get third order derivatives. 3. Homogeneous functions and Euler's theorem Definition 3.2.2 A function f(x, y) is said to be homogeneous of degree (or order) n if f(tx, ty) = tn f(x, y) for any positive t. For example (1): f(x, y) = Theorem 3.2.1 Euler's theorem If f(x, y) is a homogeneous function of degree n in x and y having continuous partial derivatives, then Proof Given f(x, y) is a homogeneous function in x and y of degree n, we can write This theorem can be extended to homogeneous function of any number of variables. If f(x, y, z) is a homogeneous function of degree n in three independent variables x, y, z and differentiable then Example 1 If u = log (x3 + y3 + z3 — 3xyz), then prove that Solution Given u = log (x3 + y3 + z3 – 3xyz) Example 2 If u = (x − y)4 + (y − z)4 + (z − x)4, then find the value of Solution Given u = (x − y)4 + (y − z)4 + (z − x)4 Example 3 If u = (x – y) (y – z) (z – x) then prove that (i) Solution Given u = (x − y) (y - z) (z - x) (ii) u is a homogeneous function of degree 3, since u (xt, yt, zt) = (tx - ty) (ty - tz) (tz - tx) = t3 (x − y) (y − z) (z − x) = t3 (x - y) (y - z) (z − x) = t3u(x, y, z) So, by Euler's theorem, we get Example 4 Solution ⸫ ƒ is a homogeneous function of degree 3 in x, y Example 5 Solution ⸫ u is a homogeneous function of degree 0 in x, y, z By Euler's theorem, we get Example 6 Solution Given u is a function of x, y, z ⸫ u(x, y, z) is a homogeneous function of degree 0 in x, y, z By Euler's theorem, we get Example 7 Solution Given u = f(x - y, y - z, z - x) Put x1 = x - y, y1 = y - z, z1 = z - x then u = f(x1, y1, z1), where x1, y1, z1 are functions of x, y, z. Example 8 Solution Example 9 Solution f(x, y) is a homogeneous function of degree 2 So, by Euler's theorem on homogeneous functions, we get Another result on homogeneous functions which follow from Euler's theorem is given below. Theorem 3.2.2 If u(x, y) is homogeneous function of degree n in x and y with all first and second derivatives continuous, then Proof Given u(x, y) is a homogeneous function of x and y of degree n. So, by Euler's theorem Differentiating (1) partially w.r.to x, we get Now differentiating (1) w.r.to y, we get Example 10 Solution Example 11 Solution = t2u(x, y) ⸫ u(x, y) is homogeneous of degree 2 and it is differentiable twice, partially. ⸫ by theorem 3.2.2, Example 12 Solution Example 13 If u = xy, then show that (i) uxy = uyx (ii) uxxy = uxyx Solution Given u = xy From (3) and (6), we get (ii) ⸫ uxxy = uxyx Example 14 Solution Example 15 Solution Given r2 = x2 + y2 + z2 Let u = f(x, y) be a function of 2 variables x, y. If x and y are continuous function of t then z will be ultimately a function of t only or z is a composite function of t. Then we can find the ordinary derivative du/dt which is called the total derivative of u to distinguish it from the partial derivatives We have Proof u = f(x, y), x = F(t), y = G(t). Giving increment Δt to t will result in increments Δx, Δy and Δu in x, y and u. Cor (1): In differential form the result (1) can be written as du is called the total differential of u. Similarly, if u = f(x, y, z) of 3 independent variable x, y, z then the total differential is Cor (2): Change of variables If u = f(x, y) where x and y are function of t1, t2 then u is ultimately a function of t1, t2 and so z is a composite function of t1, t2. Then we have partial derivatives of u w.r.to t1, t2 Cor (3): Differentiation of implicit functions The equation f(x, y) = 0 defines y implicitly as a function of x. Suppose the function f(x, y) is differentiable, then the total differential Example 1 Solution Given u = x2 y3, x = log t, y = et So u is ultimately a function of t Example 2 Solution Example 3 Solution Given u = sin-1(x - y), where x = 3t, y = 4t3 Example 4 Solution We have x = et, y = t2 Example 5 Solution Given u = x2y, x = t2, y = et Example 6 Solution Given u = cos (x2 + y2) and a2x2 + b2y2 = c2 Example 7 Solution Given z is a composite function of u and v. ⸫ we have partial derivatives of z w.r.to u and v and x = eu + e-v and y = e-u - ev Example 8 Since x and y are functions of r and θ, u is a composite function of r and θ. So we have partial derivatives of u w.r.to r, θ Example 9 Solution Given z = f(x, y) and x = eu cos v, y = eu sin v ⸫ z is a composite function of u and v. Example 10 Solution Example 11 Solution u and v can be considered as functions of x and y. We have u2 + 2v2 = 1 − x2 + y2 Differentiating partially w.r.to x, we get Differentiating partially w.r.to x, we get Example 12 Solution Given z = So, z is composite function of x. Given x3 + y3 + 3axy = 5a2 Differentiating w.r.to x, we get Example 13 If z is a function of x and y and x = u cos α - v sin α, y = u sin α + v cos α, then show that Solution Given z is a composite function of u and v and x = u cos α - v sin α, y = u sin α + v cos α Example 14 If z = f(x, y) where x = u2 - v2, y = 2uv, prove that Solution Given z = f(x, y) where x = u2 - v2, y = 2uv Since z is a function of x, y, But x and y are function of u and v So z is ultimately a function of u and v. But x = u2 - v2, y = 2uv Note: The same problem is asked as below also. If Example 15 Transform equation zxx + 2zxy + zyy = 0 by changing the independent variables using u = x - y and v = x + y Solution Given zxx + 2zxy + zyy = 0 and u = x – y, v = x + y In the given equation independent variables are x and y. We have to change them to u and v. So, we treat z as a function of u and v Substituting (2), (3) and (4) in (1), we get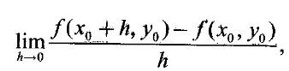 if the limit exists. Then it is denoted by
if the limit exists. Then it is denoted by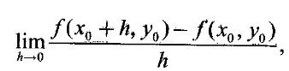
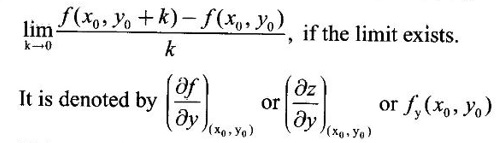
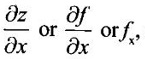 assuming the point (x, y).
assuming the point (x, y).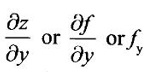
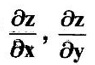
![]() at (x0, y0). represents the slope of the tangent to this curve at the point (x0, y0, z0), where z0 = f(x0, y0).
at (x0, y0). represents the slope of the tangent to this curve at the point (x0, y0, z0), where z0 = f(x0, y0).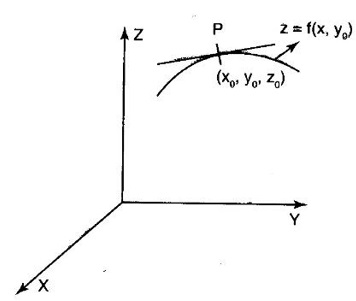
![]() at (x0, y0) is the slope of the tangent to the curve z = f(x0, y) at the point (x0, y0, z0), where z0 = f(x0, y0)·
at (x0, y0) is the slope of the tangent to the curve z = f(x0, y) at the point (x0, y0, z0), where z0 = f(x0, y0)·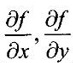 are called partial derivatives of first order, which are again functions of x, y and can be differentiated partially w.r.to x, y. These are called partial derivatives of second order and denoted by
are called partial derivatives of first order, which are again functions of x, y and can be differentiated partially w.r.to x, y. These are called partial derivatives of second order and denoted by
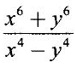 is homogeneous of degree 2.
is homogeneous of degree 2.
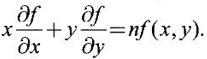

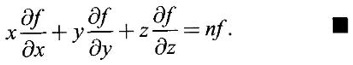
WORKED EXAMPLES
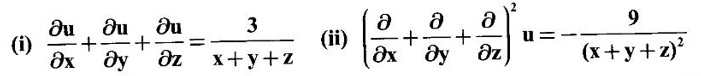

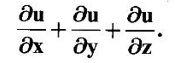

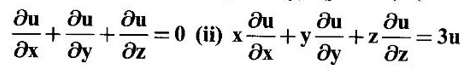

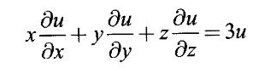




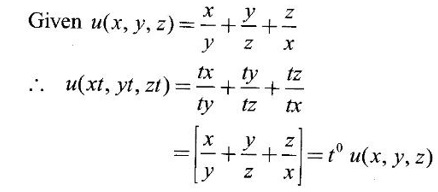
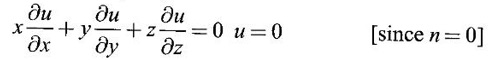

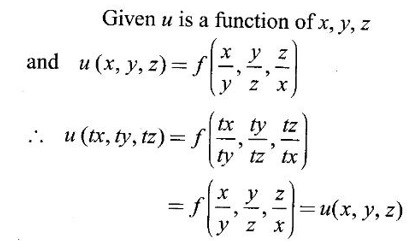
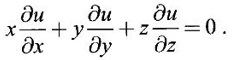
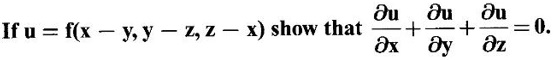




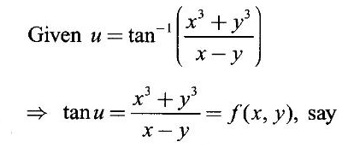
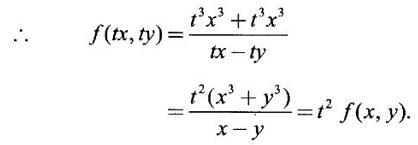

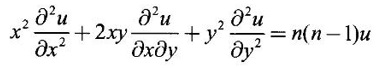



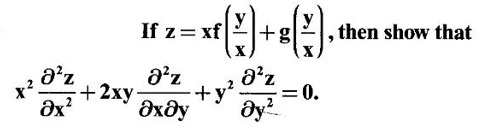



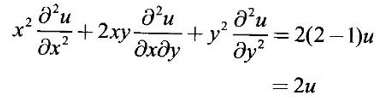
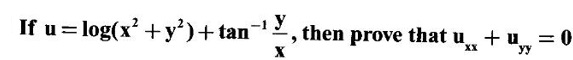


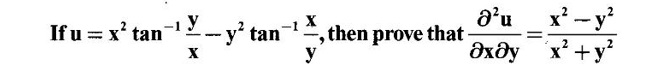



4. Total derivatives
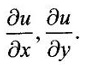
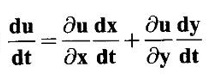

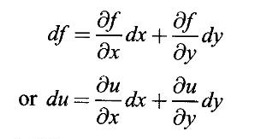
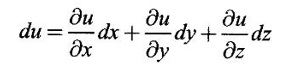
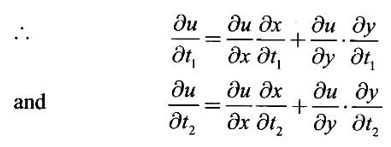
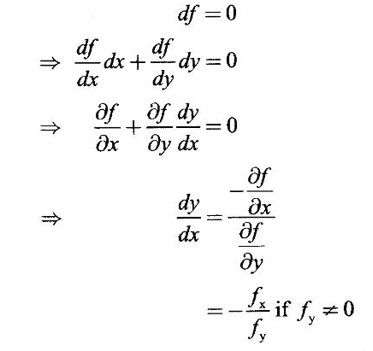
WORKED EXAMPLES
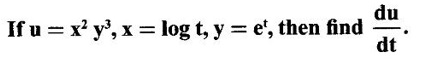

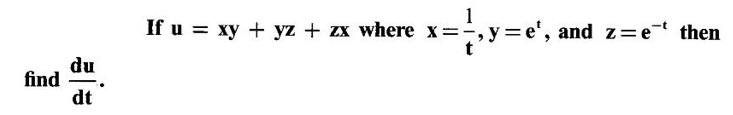

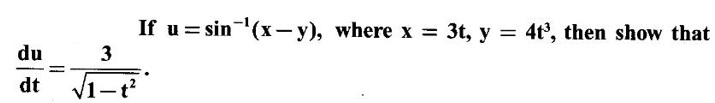

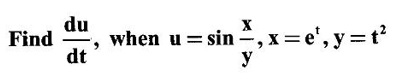


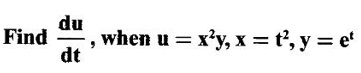



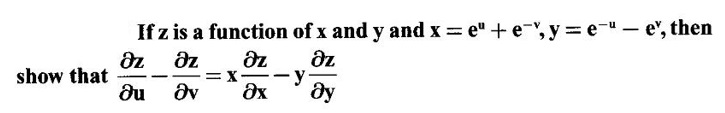

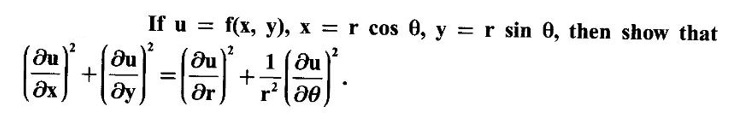 Solution
Solution 
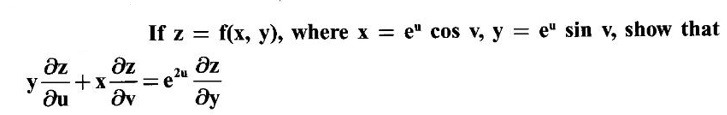
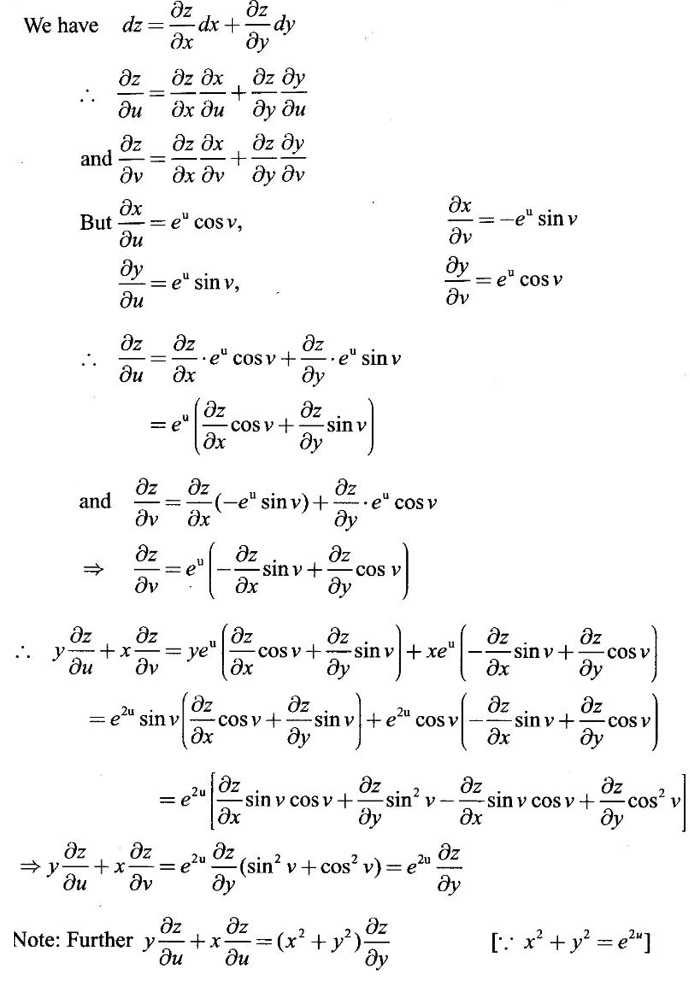
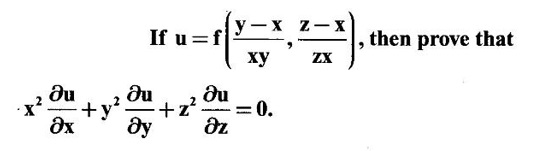

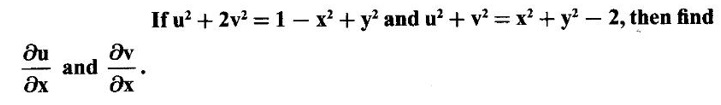
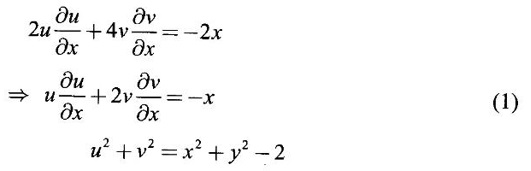

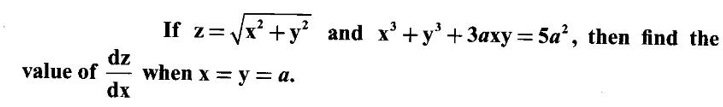
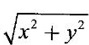 where x3 + y3 + 3axy = 5a2 is an implicit relation and y is implicitly a function of x.
where x3 + y3 + 3axy = 5a2 is an implicit relation and y is implicitly a function of x.

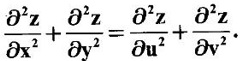

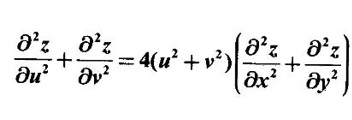

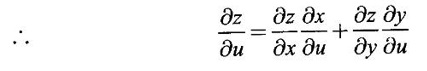

 where
where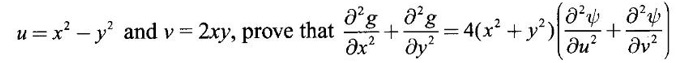


EXERCISE 3.2

ANSWERS TO EXERCISE 3.2
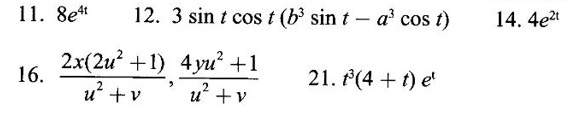
Matrices and Calculus: Unit III: Functions of Several Variables : Tag: : Definition, Theorem, Worked Examples, Exercise with Answers - Partial Derivatives
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
