Transforms and Partial Differential Equations: Unit II: Fourier Series
Odd and Even Functions
Definition, Example, Waveform, with Solved Example Problems | Fourier Series
Certain functions defined in symmetric ranges of the form (−л, л), (−l, l) can be classified as even and odd functions.
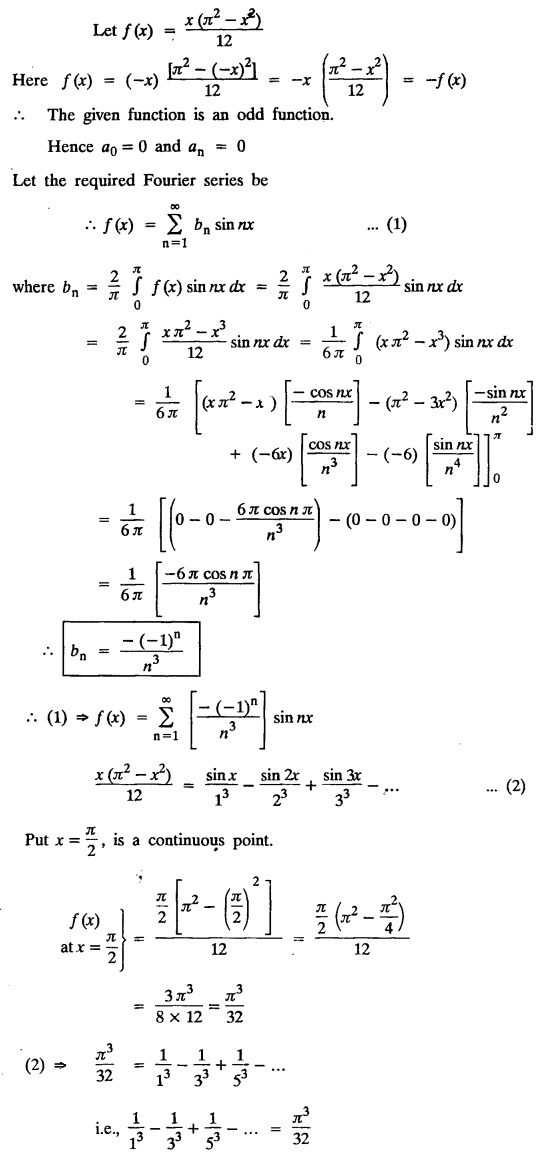
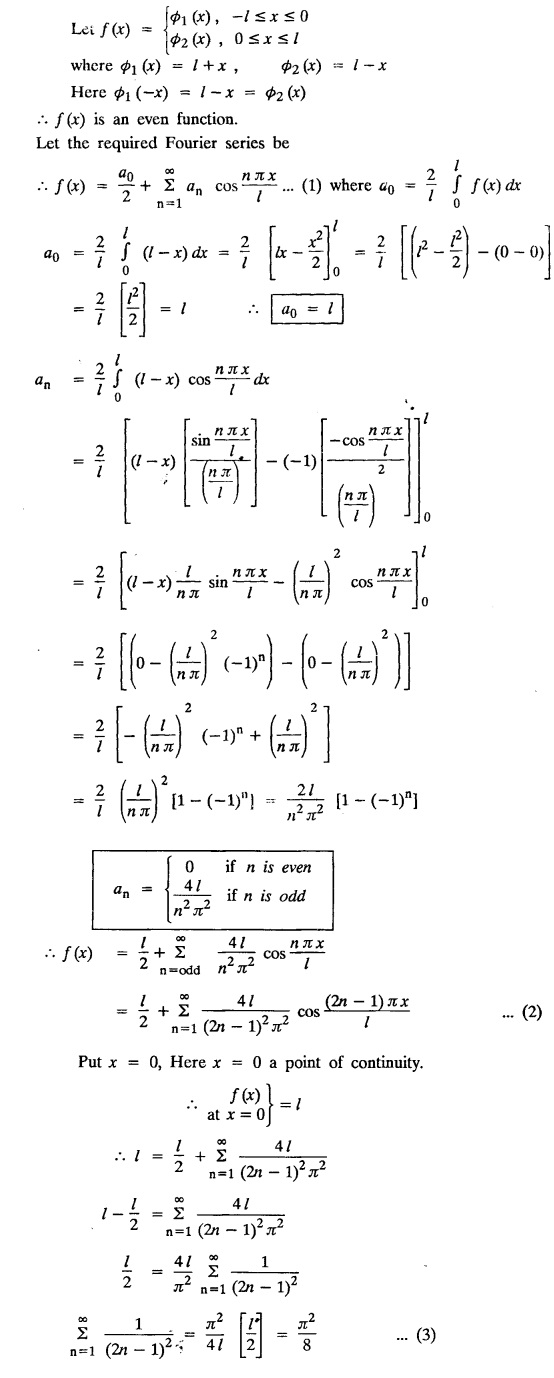
ODD AND EVEN FUNCTIONS Certain functions defined in symmetric ranges of the form (−л, л), (−l, l) can be classified as even and odd functions. Note 1: Functions defined in (-л, л) and (-l, l) may be either even or odd. 2. Functions defined in non-symmetric range like (0, 2π), (0, 2l) the case even or odd does not arise. f(x) is said to be an even function of x in (−l, l) if f(−x) = ƒ (x) Geometrically, the graph of an even function will be symmetrical with respect to Y axis. f(x) is said to be an odd function of x in (-l, l) if ƒ(-x) = -f(x) Geometrically, the graph of an odd function will be symmetrical about the origin. Example: sinx, x3, x cos x Example 2.2.1 : What are the values of the Fourier constants when an even function f(x) is expanded in a Fourier Series in the interval – π to π? Solution : Example 2.2.2: What are the values of the Fourier constants when an odd function f(x) is expanded in a Fourier Series in the interval –π to π? Solution : Example 2.2.3: What are the values of the Fourier constants when an even function f(x) is expanded in a Fourier Series in the interval -l to l? Solution : Example 2.2.4: What are the values of the Fourier constants when an odd function ƒ (x) is expanded in a Fourier series in the interval -l to l? Solution: Example 2.2.5: What are the values of the Fourier constants when f(x) is neither even nor odd in a Fourier series in the interval -л to л? Solution : Let the Fourier Series for f (x) in (-л, л) be Formulas (1), (2) and (3) are known as the Euler formulas. Example 2.2.6: What are the values of the Fourier constants when f(x) is neither even nor odd in a Fourier series in the interval -l to l ? Solution : The Fourier expansion for f (x) in the interval – l < x < l is given by Example 2.2.7: Find bn in the expansion of x2 as a Fourier Series in (-л, л). Solution : Given f (x) = x2 is an even function in the interval (− π, π) ⸫ bn = 0 Example 2.2.8: If f(x) is an odd function defined in (-l, l), what are the values of a0 and an? Solution : Given f(x) is an odd function in the interval (-l, l) ⸫ a0 = 0, an = 0 Example 2.2.9 : Find the Fourier constants bn for x sin x in (− π, π). Solution: Example 2.2.10 : Determine the value of an in the Fourier series expansion of f(x) = x3 in −л < x < л. Solution : Let f(x) = x3 f(-x) = (−x)3 = -x3 = -f(x) Therefore f(x) is an odd function. Hence a0 = 0 and a0 = 0 § Note: Example 2.2.11 Classifiy the functions as even, odd or neither. Solution : Example 2.2.12. Classify the following functions as even, odd or neither. Solution: Example 2.2.a(: Find the Fourier expansion of f(x) = x in - л < x < л. Solution: Let f (x) = x, ƒ (−x) = −x = -f(x) Therefore f(x) is an odd function in (-л, л) Example 2.2.a(2): Find the Fourier series for f(x) = x2 in –л ≤ x ≤ л and deduce that Solution: Given: f(x) = x2, ƒ(−x) = (−x)2 = x2 = f(x) Therefore f(x) is an even function in (-л, л). Hence bn = 0 Example 2.2.a(3): Solution: Example 2.2.a(4): What is the Fourier expansion of the periodic function whose definition of one period is Solution: Example 2.2.a(5): In л < x < л, express sinh ax and cosh ax in Fourier series of periodicity. Solution: (i) Let f (x) = sinh ax (i) Let f (x) = cosh ax Example 2.2.a(6): Obtain the Fourier series of periodicity 2л for f(x) = -x, when л < x < 0 and f(x) = x, when 0 < x < л [OR] Obtain the Fourier series to represent the function. f (x) = |x| in - л < x <л and deduce that Solution: Example 2.2.a(7): Find the Fourier series representation for f(x) = | sinx | in –л < x < л Solution: Example 2.2.a(8) Express f(x) = xsinx as a Fourier series in (-л, π). Solution: Given f(x) = x sin x Example 2.2.a(9) : Expand f(x) = | cos x | in a Fourier series in the interval (-л, π). Solution: Example 2.2.a(10): Determine the Fourier series for the function Solution: Example 2.2.a(11): Obtain the Fourier series for f(x) = 1 + x + x2 in (-л,л). Deduce that Sol. Example 2.2.a(12): Prove that Solution: EXERCISE 2.2.(a) Problems under the interval (−π, π) 2.2 (b) PROBLEMS UNDER THE INTERVAL (-l, l) Example 2.2.b(1) If f(x) = x is defined in -l < x < l with period 2l, find the Fourier expansion of f(x). Solution : f(x) = x f(-x) = -x = - f(x) Therefore f(x) is an odd function. Hence a0 = 0 and an = 0 Let the required Fourier series be Example 2.2.b(2) : Obtain the Fourier series for the function given by Solution: Example 2.2.b(3). Expand f(x) = e-x as Fourier series in (-1, 1). Solution: Example 2.2.b(4): Find the Fourier series expansion of the periodic function f(x) of period 2l defined by Sol. Given interval is (-l, l) Example 2.2.b(5): Find the Fourier series expansion the following periodic function of period 4, Solution : In the above problem Put l = 2 Problems under the interval (−l, l) 1. Obtain the F.S. for f(x) defined in (-1, 1) by 2. Find the F.S. for the function 3. f(x) is defined in (-2, 2) as follows. Express f(x) in a F.S. of periodicity 4. 13. Find the Fourier series expansion of ƒ(x) in (−2, 2) which is defined as follows.Definition :

Definition :

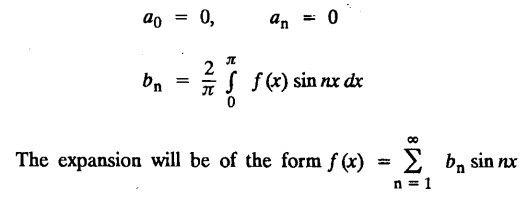
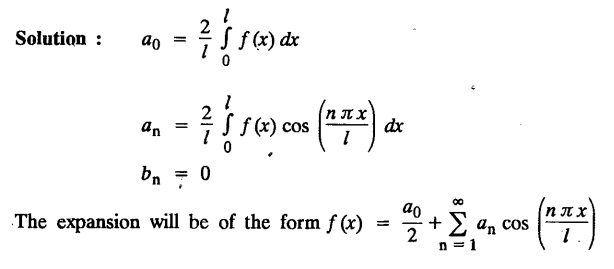
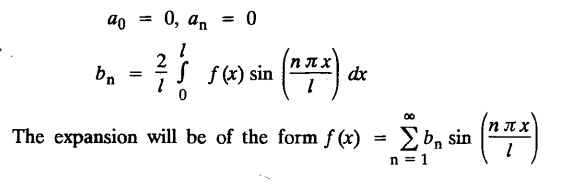
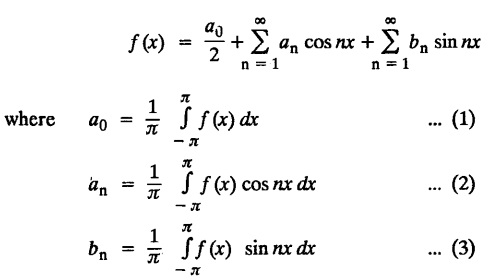
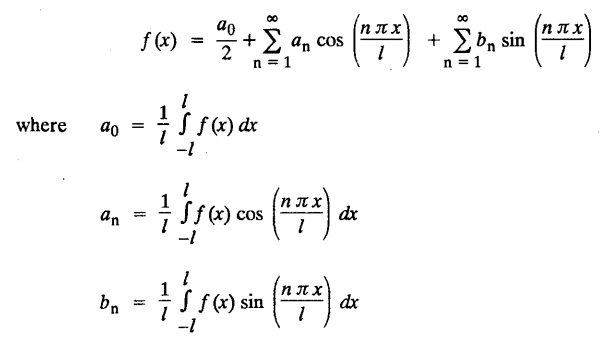
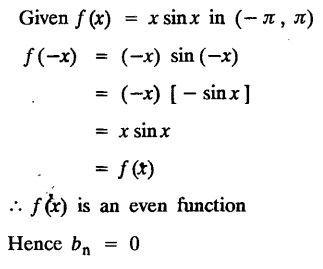
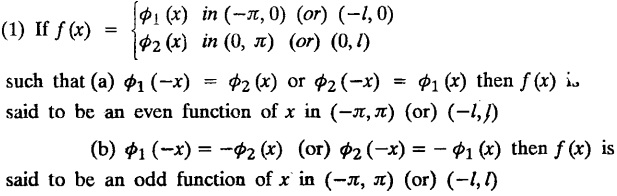
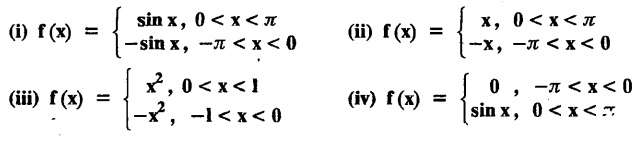
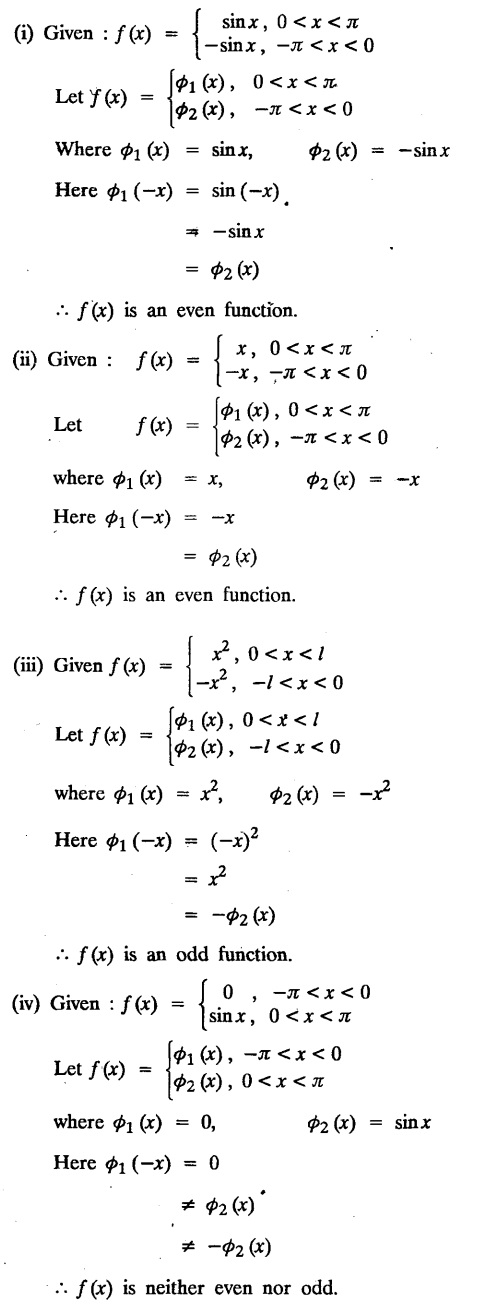
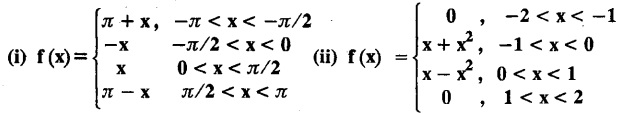
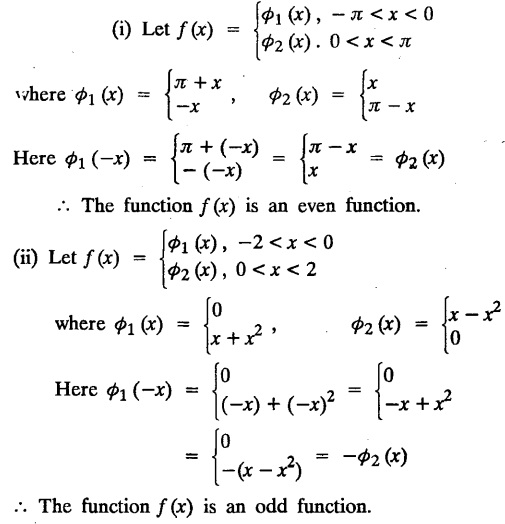
2. (a) PROBLEMS UNDER THE INTERVAL (—л, л)

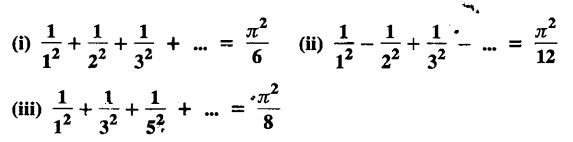



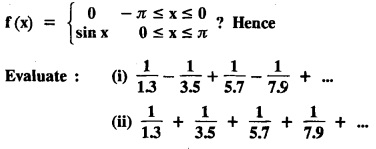
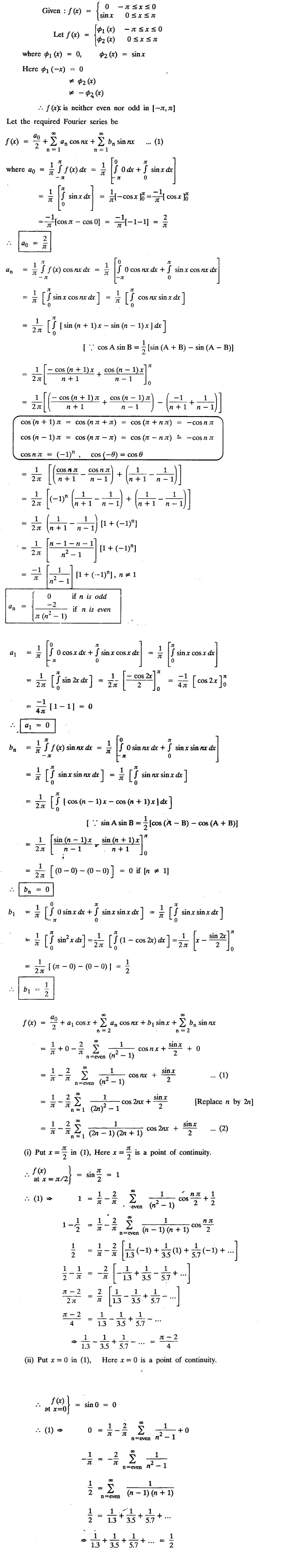
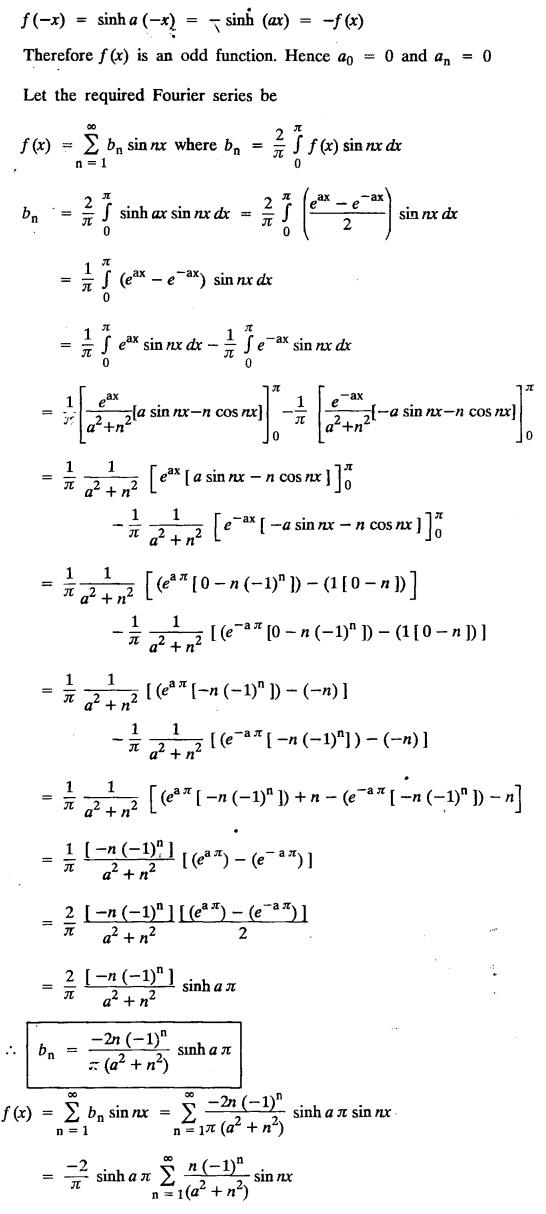

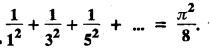
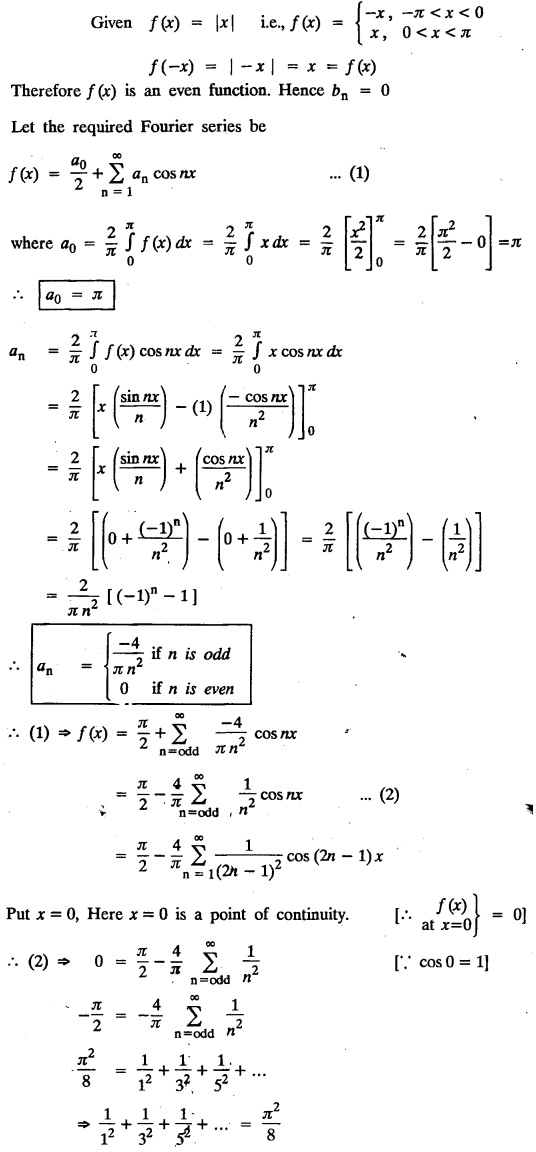



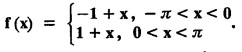
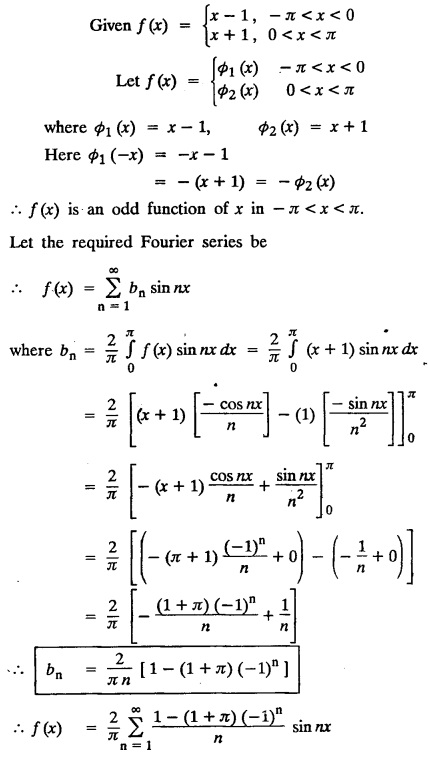
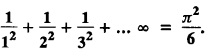

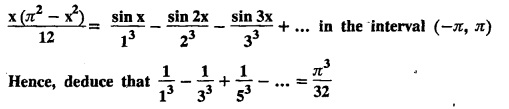


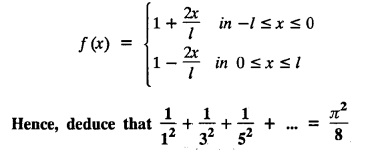
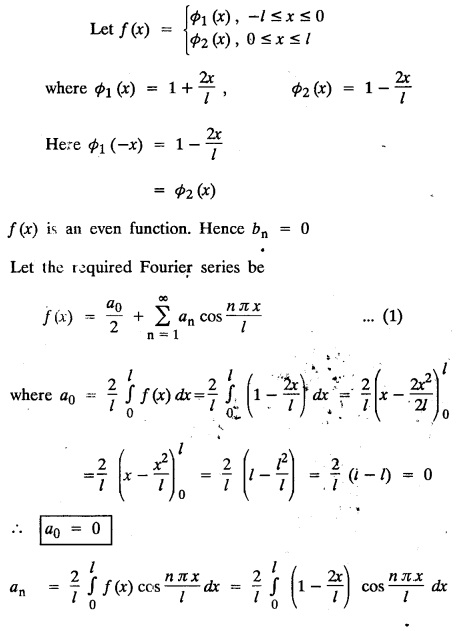


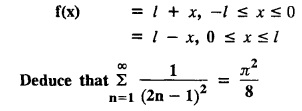
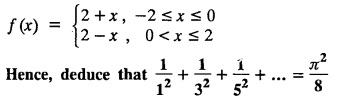
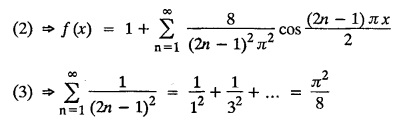
EXERCISE 2.2.(b)
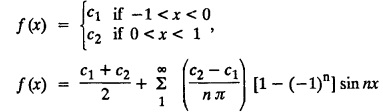
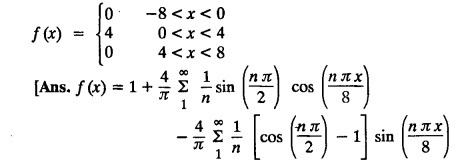

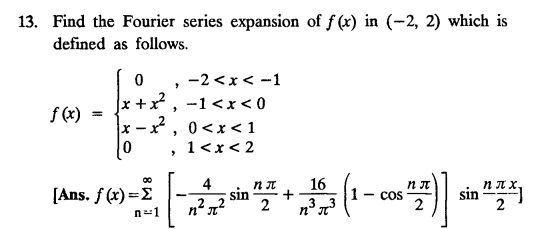
Transforms and Partial Differential Equations: Unit II: Fourier Series : Tag: : Definition, Example, Waveform, with Solved Example Problems | Fourier Series - Odd and Even Functions
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
