Number Systems

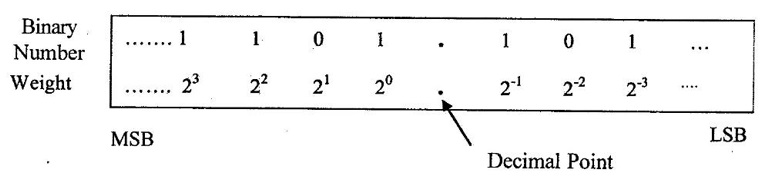
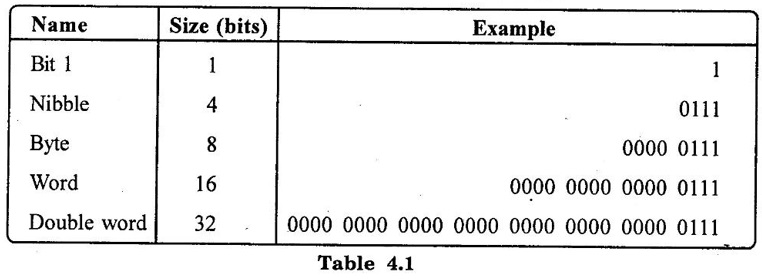
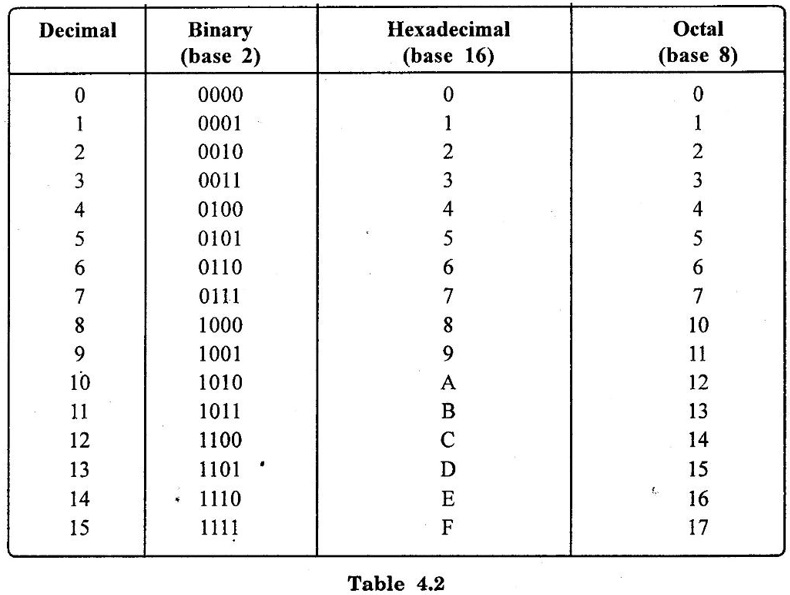
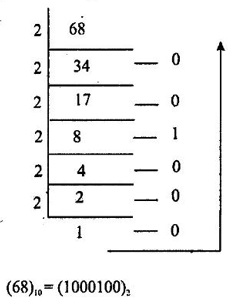
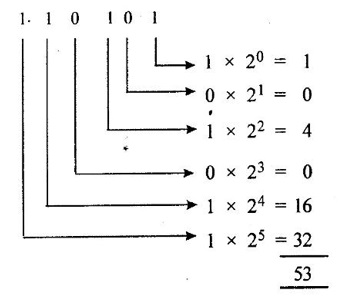
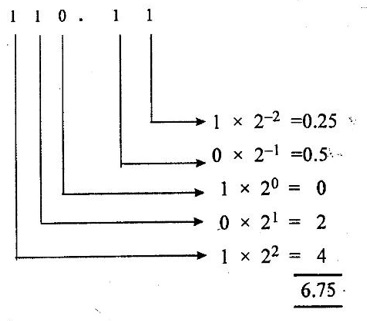
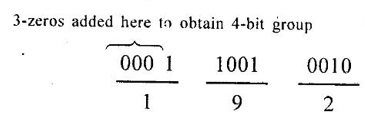
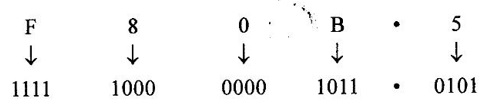
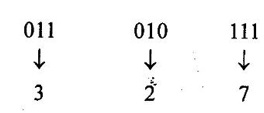
NUMBER SYSTEMS

• Number system is basis for counting various items. For writing any number exceeding 9, an array of digits are used. Some of the commonly used number systems are decimal, binary, octal and hexadecimal number system.

(i) Decimal numbers are used to represent quantities outside the digital system.

(ii) Binary number system is extensively used in digital computers.

(iii) Octal system has certain advantages in digital work as it needs less circuitry to get information into and out of a digital system.

(iv) Hexadecimal number system is used in microcomputers.

1. Decimal Number System

Decimal number system has a base of 10 and is a position value system. The statement the decimal number system has a base of 10 implies that it contains ten unique symbols i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Let us consider a decimal number say 2345.6. We know that it can be represented as under:

2000 + 300 + 40+ 5 + 0.6 = 2345.6

2 × 103 + 3 × 102 + 4 × 101 + 5 × 100 + 6 × 10-1 = 2345.6

The decimal number 2345.6 can also be written as (2345.6)10 where 10 subscript indicates the radix or base. The powers of 10 are incremented from zero by one as the position is moved successively toward the left from the decimal point. Further more the coefficients of the powers of 10 are allowed to take on values from 0 to 9.

The left most digit has greatest weight is called the most significant digit and right most digit has least weight is called the least significant digit.

2. Binary Number System

Binary system with its two digit is a base two system. The two binary digits are 1 and 0. Each binary digit commonly known as bit, has its own value or weight.

In binary system weight is expressed as a power of 2, as shown below.

Example

Represent the binary number 1101.101 in power of 2 and find its decimal equivalent.

N = 1×23 + 1×22 + 0×21 + 1×20 + 1×2−1 + 0×2-2 + 1×2-3

= 8 – 14 + 0 + 1 + 0.5 + 0 + 0.125

N = (13.625)10.

Binary Number Formats

Some of the binary number formats are listed as follows:

In any number base, we may add as many leading zeros as we wish without changing its value.

The Bit: The smallest unit of data defined as a single bit.

The Nibble: A Nibble is a combination of four bits.

The Byte: A byte is a combination of eight bits.

The Word: A word is a combination of 16 bits.

The Double word: The double word its name implies two words.

The double word quantity is 32 bits. The double word can be divided into two; a higher order word and a lower order word, four bytes or eight nibbles.

3. Octal Number System

The number system with base eight is known as octal number system and it uses eight digits of decimal number system 0, 1, 2, 3, 4, 5, 6 and 7. The digit position in octal number have weights as follows.

Each digit in octal number has weight. As it is a base-8 system, the weights starting from LSB towards MSB will be 80, 81, 82... for integer part and 8-1, 8-2, 8-3... for fractional part.

4. Hexadecimal Number System

The hexadecimal system has a base of 16 having 16 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F.

It is another number system that is particularly useful for human communications with computer. One hex digit is equivalent to four bits. The digit positions in hexa decimal number have weights as follows.

Relationship between decimal, binary, hexadecimal and octal.

5. Code Conversion (Decimal to Binary Conversion)

Problem 4.1

Convert decimal (68)10 to binary number.

Problem 4.2

Convert decimal (13.125)10 to binary number.

Ans. (13.125)10 = 101.0012

Problem 4.3

Convert binary 110101 to decimal.

Ans. (110101)2 = 5310

Problem 4.4

Convert 110.112 into decimal.

Ans. (110.11)2 = (6.75)10

Binary to Hexa decimal conversion

The binary number is grouped into group of 4-bits from LSB to MSB and each group is replaced by its hex representation. Zeros are added as required to complete a 4-bit group of MSB.

Problem 4.5

Convert binary number (110010010)2 to hexadecimal number.

Solution :

The binary number is grouped into groups of 4-bits LSB to MSB. Additional zeros to be added at MSB if necessary. In this example 3 zeros are added at MSB to obtain 4-bit group.

Ans. (110010010)2 = 19216

Problem 4.6

Convert binary number (11001111)2 to hexadecimal number.

Solution :

Ans. (11001111)2 = (CF)16

Binary to Octal conversion

Hexadecimal to binary conversion

Hex numbers can be converted into equivalent binary number by replacing each

hex unit by its equivalent 4-bit binary number.

Problem 4.7

Convert hexadecimal (F80B.5)16 into binary.

Solution :

(F 8 0 B)16 (1111 1000 0000 1011 • 0101)2

Hexadecimal to decimal conversion

A hexa decimal number can be converted into its decimal equivalent by multiplying each hex digit by its weight and the taking the sum of products.

Problem 4.8

Convert (345)16 into decimal equivalent.

Solution:

345 = 3×162 + 4×161 + 5×160

= 768 + 64 + 5 = (837)10

Decimal to Hexa decimal conversion

A decimal number can be converted into an equivalent hexadecimal number by progressively dividing the integer part of the decimal number by 16 and noting the reminders till we reach 0 and arranging the remainders in reverse order. Similarly, by progressively multiply the decimal fraction by 16 and noting the carrys till the result of multiplication is 0 or desired number of digits have been obtained and then arranging these carrys in forward order.

Problem 4.9

Convert decimal (453.35)10 into hexadecimal.

Solution :

(453)10 → (1 12 5)16 = (1 C 5)16

Finally, (453.35)10 = (1C5.59)16

Hexadecimal to octal conversion

Problem 4.10

Convert (A6F. CD)16 into octal.

Solution :

Converting into binary we have,

Converting to octal we have,

So, (A6F. CD)16 = (5157.632)8

Binary to octal conversion

The binary number is grouped into groups of 3 bits from LSB to MSB and each group is replaced by its hex representation. Zeros added as required to complete a 3-bit group.

Problem 4.11

Convert binary number (11010111)2 into octal number.

Solution:

Hence, (11010111)2 = (327)8

Octal to binary conversion

Problem 4.12

Convert octal number (375:37)8 into binary number.

Solution :

(375.37)8 = (011 111 101 • 011 111)2

Octal to Hexadecimal conversion

Problem 4.13

Convert octal (641)8 into binary equivalent.

Solution :

(641)8 = (1A1)16

Octal to Decimal conversion

Problem 4.14

Convert octal (630.4)8 to decimal.

Solution :

(630.4)8 = 6×82 + 3×81 + 0×80 + 4×8-1

= 384 + 24 + 0 + 0.5

= (408.5)10

Decimal to octal conversion

Problem 4.15

Convert decimal (6089.25)10 into octal.

Solution:

(6089)10 = (13711)8

Hence, (6089.25)10 = (13711.2)8