Engineering Physics: Unit IV: Basic Quantum Mechanics
Normalisation of Wave Function
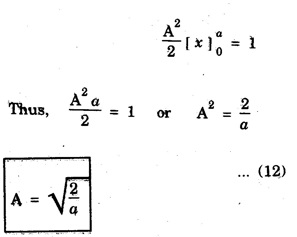
The constant A is determined by normalisation of wave function as follows.
NORMALISATION OF WAVE FUNCTION The constant A is determined by normalisation of wave function as follows. It is certain that the particle is some where inside the box. Thus, the probability of finding the particle inside the box of length a is given by The second term of the integral becomes zero at both limits On substituting. eqn (12) in egn (9), we have The eigen function (Ψn) belongs to eigen energy values En and it is expressed as This expression (13) is known as normalised eigen function. The energy En and normalised wave functions Ψn are shown in .fig. 6.10. Special cases From eqns (8) and (13), the following cases can be taken and they explain the motion of electron in one dimensional box. Hence, Ψ1 (x) is maximum at exactly middle of the box as shown in fig. 6.10. Hence, Ψ2 (x) is maximum at quarter distance from either sides of the box as shown in 6.10. Hence, Ψ3 (x) is maximum at exactly middle and one-sixth distance from either sides of the box as shown in fig. 6.10.

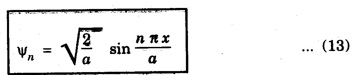

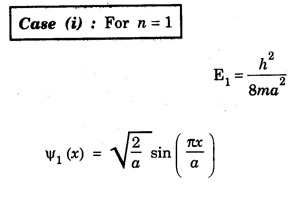
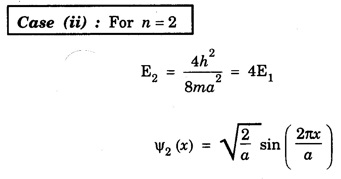
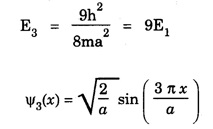
Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : - Normalisation of Wave Function
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
