Engineering Mechanics: Unit V: Dynamics of Particles
Normal and Tangential Components (Path Variables)
with Solved Example Problems | Curvilinear Motion
Consider a particle moving along a curved path as shown in Fig. 9.8.1.
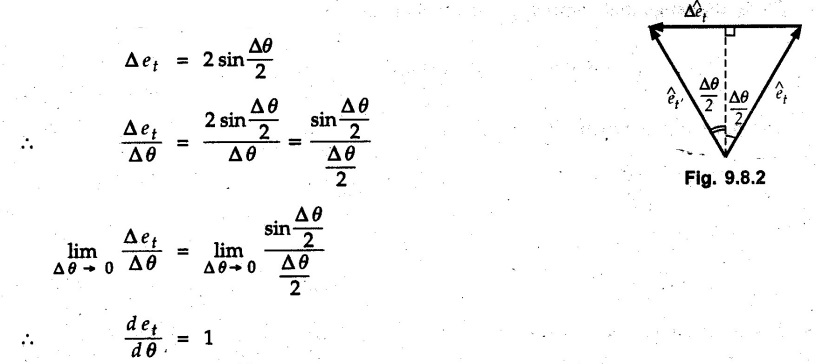
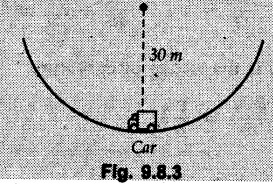
Normal and Tangential Components (Path Variables) • Consider a particle moving along a curved path as shown in Fig. 9.8.1. The tangential unit vector êt is along the tangent to the curve and normal unit vector ên is perpendicular to êt directed towards the centre of curvature. • When particle travels along the curved path from P to P' in time At, the tangential unit vector changes from êt to êt. • The change in tangential unit vector is Δ êt = êt - êt as shown in Fig. 9.8.2. • As magnitude of êt is 1, • Also, as Δθ → 0, Δ êt becomes perpendicular to êt. • Since velocity of particle is tangential, v = v êt where v = Magnitude of velocity, i.e. speed. The normal component of velocity is always zero. • Here, the tangential component of acceleration is • The normal component of acceleration is • The magnitude of acceleration is Example 9.8.1 An automobile is being driven along a circular track of diameter 'd'. Determine the value of 'd' if the normal component of acceleration is 2 m/s2 for a speed of 60 km/h. Solution : Example 9.8.2 A car is moving with constant speed along a circular path of radius 30 m. If for safety considerations, the acceleration is not to exceed 4 g, determine the maximum speed of the car. Refer Fig. 9.8.3. Solution : Given ρ = 30 m, at = 0 (constant speed) Example 9.8.3 A car starts from rest on a circular curve of 250 m radius and accelerates at a constant tangential acceleration 1.2 m/s2. Determine distance travelled and time taken when magnitude of total acceleration of car becomes 1.5 m/s2. Solution: Given at = 1.2 m/s2 (constant) a = 1.5 m/s2 As tangential acceleration is constant, we can use kinematical equations in tangential direction. u = 0, v = 15 m/s, a = 1.2 m/s2 Example 9.8.4 A car moves on a circular path of radius 25 m, with a uniform speed of 9 m/s. Determine the total acceleration of the car. Solution: As speed is constant, at = 0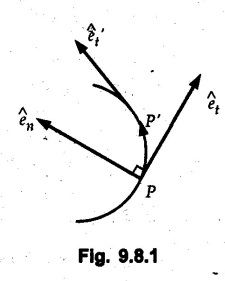


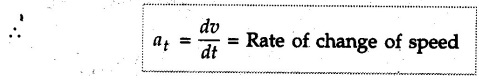


Solved Examples for Understanding
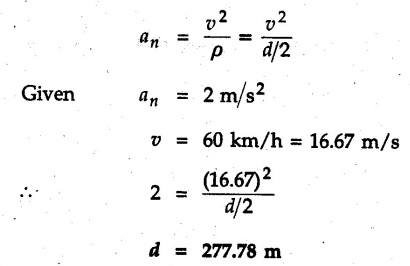
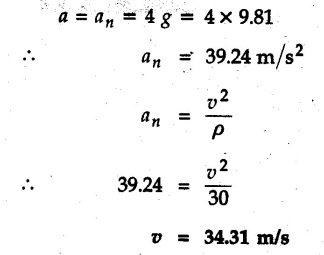

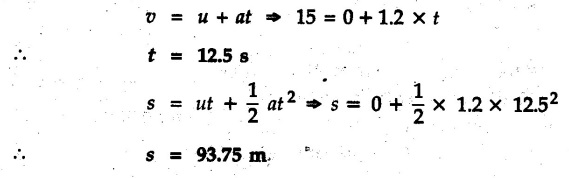
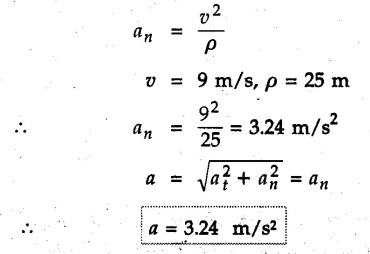
Engineering Mechanics: Unit V: Dynamics of Particles : Tag: : with Solved Example Problems | Curvilinear Motion - Normal and Tangential Components (Path Variables)
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
