Matrices and Calculus: Unit II: Differential Calculus
New Functions from given functions
Definition, Solved Example Problems | Differential Calculus
In this section we discuss some of the main ways of getting new functions from given functions.
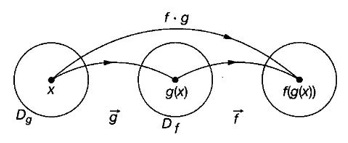
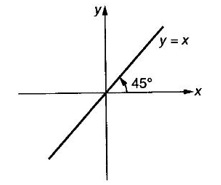
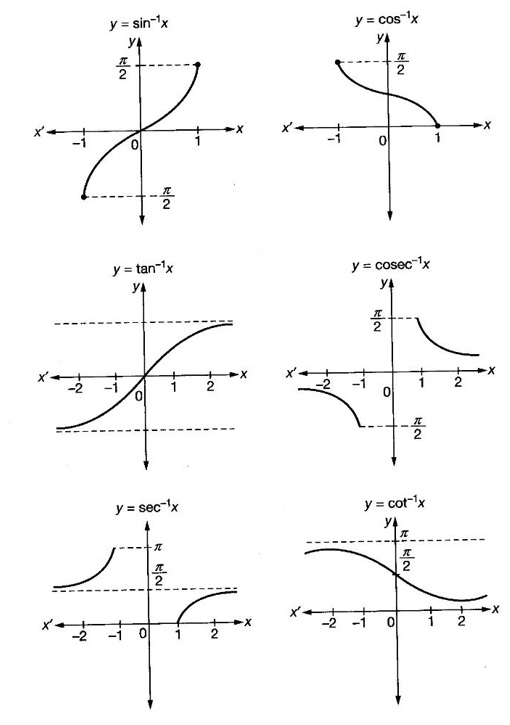
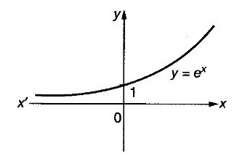
NEW FUNCTIONS FROM GIVEN FUNCTIONS In this section we discuss some of the main ways of getting new functions from given functions. We will also see some standard functions frequently used in subsequent topics. Definition 2.5 Sum, Product and quotient of functions Let f and g be given functions with domains Df and Dg. Then their sum f + g, difference ƒ-g, product fg and quotient f/g are defined as below. (cf)(x) = cf(x) ∀x ∈ Df, c is a constant Example 1 Let f(x) = Find the formulas for Solution Given f(x) = f(x) is real if x – 2 ≥ 0 ⇒ x ≥ 2 Definition 2.6 Equal functions Two functions ƒ and g are equal and written as ƒ = g if and only if (i) ƒ and g have same domain i.e., Df = Dg and (ii) f(x) = g(x) ∀x ∈ Df Example 2 Test the equality of the functions of ƒ and g defined by Solution Given f(x) = we know ⸫ Df = Dg and the values at any point in Df are the same for ƒ and g ⸫ f = g Example 3 Let f(x) = Solution Given f(x) = Definition 2.7 Composition of functions Given the functions ƒ and g with domains Df and Dg. Their composition (ƒ ◦ g)(x) =ƒ(g(x)) ∀ x ∈ Dg for which g(x) is in Df (ƒ◦g) is read as "f composite g" or "f composed with g" or "composition f with g" In ƒ◦g, the function g acts first, then ƒ. In general, ƒ◦g ≠ g◦f WORKED EXAMPLES Example 4 If f(x) = √x and g(x) = x + 1 find (i) (f•f)(x) (ii) (g•g)(x) (iii) (ƒ•g)(x) (iv) (g•ƒ)(x) Solution We notice that (ƒ·g)(x) = (g⋅ƒ)(x) ⇒ ƒ·g ≠ g · ƒ So, the operation of composition of functions is not commutative. Definition 2.8 If two functions ƒ and g satisfy the conditions g(f(x)) = x∀x∈Dƒ and f(g(x)) = x ∀ x ∈Dg, then we say ƒ and g are inverse functions. i.e., f is the universe of g and g is the universe of f If g is the inverse of f, then we write g = ƒ-1 Note (i) g(f(x)) = x ⇒ (g⋅ ƒ)(x) = x ⇒ g⋅f is identify on Df and f⋅g is identity of Dg. (ii) domain of f-1 = range of ƒ (iii) A function ƒ is one-one if any line parallel to x-axis meets the graph of ƒ in almost one point If y = f(x) is a one-one function i.e., x1 ≠ x2 ⇒ f(x1) ≠ f(x2)for any x1, x2 ∈ Df then solve the equation for x in terms of y i.e., x = g(y) provides the inverse of ƒ-1 ⸫ x = f-1(y) So, in the given equation y = f(x) and inverse equation x = f-1 (y), the roles of x and y interchanged. Geometrically, the graph of f-1 is the reflection of the graph of ƒ in the line y = x Example 5 If f(x) = Solution Given f(x) = To find inverse: Clearly for different values of x, we have different values for f(x). So, f is 1 – 1 Example 6 Let f(x) = Solution We shall now list some common functions that will be discussed frequently in different contexts. 1. Constant function A function ƒ defined by f(x) = C, where C is a fixed constant, is called a constant function. Df = ℝ, Rf = {C}. Graph is a straight line y = C parallel to x-axis 2. Identity function A function ƒ defined by f(x) = x is called Identity function. Df = ℝ, Rf = ℝ. Graph is y = x. 3. Linear function A function ƒ defined by f(x) = ax + b, where a and b are constants, is called a linear function Df = ℝ, Rf = ℝ. Graph is a straight line y = ax + b 4. Power function For a fixed positive integer n, the function f is defined by f(x) = xn is called a power function Df = ℝ, Rf = ℝ. 5. Polynomial function A polynomial function P is defined by where a0, a1,..., an are constant coefficients and n is an integer ≥ 0 The expression a0xn + a1xn-1 +,..., an is called a polynomial in x. If a0 ≠ 0, then n is called the degree of the polynomial. Domain DP = ℝ. If n = 2, 3, 4, the polynomials are respectively called quadratic, cubic and quartic polynomials. The graph of a quadratic polynomial y = ax2 + bx + c is a parabola. 6. Rational function A rational function f is a ratio or quotient of two polynomial functions, Df = the set of real x for which q(x) ≠ 0 For example Df = ℝ - {−2, 2} 7. Algebraic functions Any function that can be constructed from polynomials by finitely many algebraic operations such as addition, subtraction, multiplication, division and root extraction are called algebraic functions. For example 8. Trigonometric functions 9. Inverse trigonometric functions The graph of these inverse trigonometric functions are given below. 10. Exponential function A function ƒ defined by f(x) = ax, where a > 0, a ≠ 1, is called an exponential function with base a. Among all possible bases the base e is special in calculus. The function f(x) = ex is called the natural exponential function. Domain ƒ = (-∞, ∞), range = (0, ∞) The graph y = ex is shown here. 11. Logarithmic function The function f defined by f(x) = loga x, x > 0 and a > 0, a ≠ 1 is called the logarithmic function with base a. The most important logarithmic function in application is f(x) = loge x which is called the natural logarithmic function. It is also known as Naperian logarithm. logex is usually written as In x. Domain = (0, ∞), range (−∞, ∞) Note: (i) Exponential function ax and logarithm function loga x are inverse functions with a > 0, a ≠ 1 . If f(x) = ax, then f-1(x) = loga x. The graph of y = loge x. is shown here ex and loge x are inverse functions. If we draw the graph of y = ex and y = loge x in the same figure. We will see y = loge x is the reflection of y = ex in the line y = x. 12. Transcendental functions Functions that are not algebraic are called transcendental functions. Trigonometric functions, inverse trigonometric functions, exponential functions and logarithmic functions are transcendental functions. EXERCISE 2.2 ANSWERS TO EXERCISE 2.2
 where domain of f/g is the set of all x ∈ Df ∩ Dg such that g(x) ≠ 0.
where domain of f/g is the set of all x ∈ Df ∩ Dg such that g(x) ≠ 0.WORKED EXAMPLES
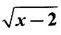 and g(x) = x - 3
and g(x) = x - 3

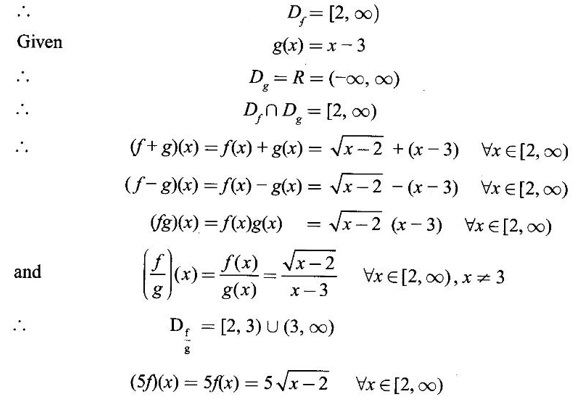
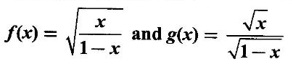


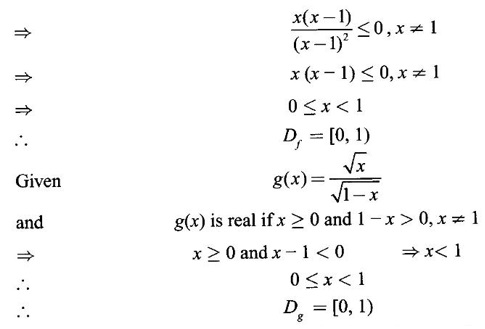
 and g(x) =
and g(x) = 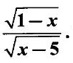 Test whether f = g?
Test whether f = g?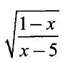

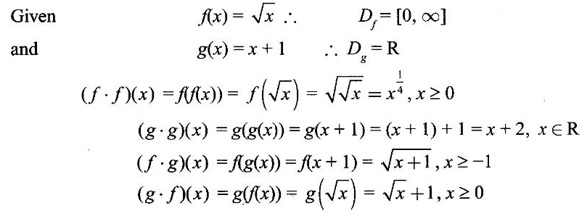
1. Inverse Function
2. Procedure to Find Inverse Function
WORKED EXAMPLES
 find the inverse of f-1 and its domain.
find the inverse of f-1 and its domain.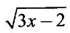


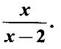 Find a function y = g(x) such that (ĥg)(x) = x.
Find a function y = g(x) such that (ĥg)(x) = x.
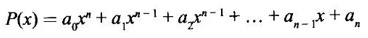
 where p and q are polynomial functions
where p and q are polynomial functions is a rational function, being the ratio of two polynomials.
is a rational function, being the ratio of two polynomials. algebraic functions.
algebraic functions.

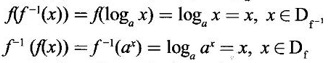



Matrices and Calculus: Unit II: Differential Calculus : Tag: : Definition, Solved Example Problems | Differential Calculus - New Functions from given functions
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
