Engineering Physics: Unit I: Mechanics
Multiparticle dynamics
Definition, Examples, Equations
A mechanical system consists of two or more particles is called multiparticle system.
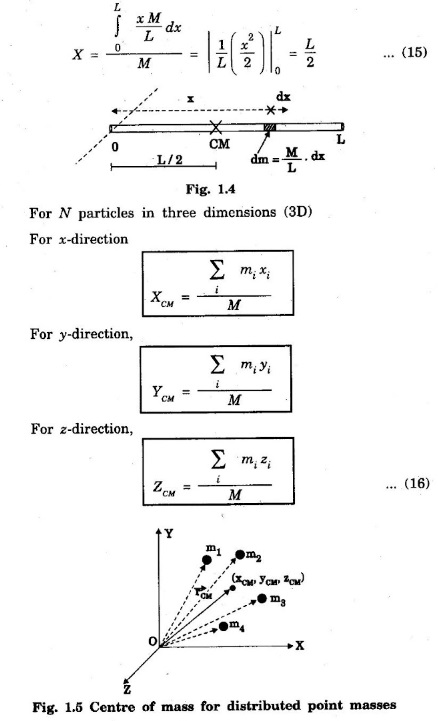
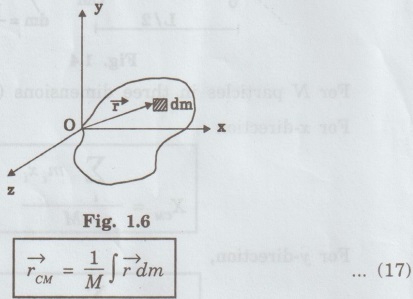
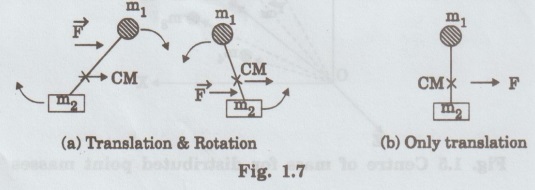
MULTIPARTICLE DYNAMICS A mechanical system consists of two or more particles is called multiparticle system. Let us consider two particles of mass m, and m, moving in one-dimension with co-ordinates x1 and x2, as shown in fig. 1.2. where Eqn (1) becomes Similarly, for particle 2, Total force on system of the two particle is given by adding Eqns (3) and (4), we get where Let the total mass of the system (body) be equal to M = m1 + m2 ... (8) Multiplying and dividing eqn (7) by M in L.H.S, is called the center of mass (CM). Thus, CM has a location X which is a weighted average of x1 and x2: lies midway between the two particles. If m1 > m2, then X is closer to x1 and vice-versa. According to eqn.(10), CM is a fictitious body whose acceleration is controlled by only the external force and not by the internal forces between the particles. In general, the CM for a system (body) of N number of particles is obtained by extending eqn (1) as For a continuous distribution of masses, for example in a one-dimension, the CM is represented as Here, we consider an infinite sum. Further for continuous distribution of mass, the summation is changed into integration. Example So in the case of a uniform rod Mass per unit length of the rod = M/L Mass of the elemental length dx of the rod Mass of the whole length of the rod is obtained by integrating between limits x = 0 and x = L) Thus in vector rotation and for continuous object as shown in fig. 1.6. Consider the motion of a system consisting of a large number of particles. There is one point in it which behaves as though the entire mass of the system were concentrated there and all the external forces were acting at this point. This point is called the centre of mass of the system. Note The external force acting on a system (body) at an arbitrary point (other than CM), produces both rotational and translational motions. On the other hand the force acting at CM of a system produces only translational motion.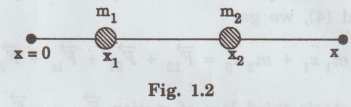
![]() is the force acting on body m1, then according to Newton's Law,
is the force acting on body m1, then according to Newton's Law,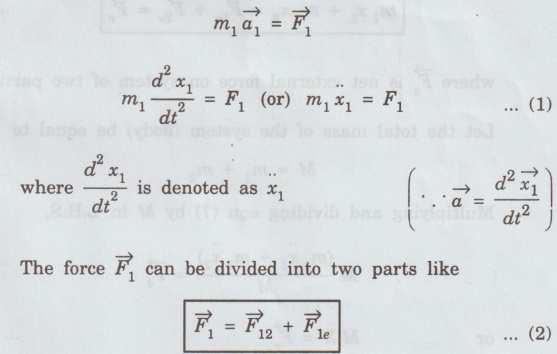
![]() is the internal force on particle 1 by particle 2.
is the internal force on particle 1 by particle 2. ![]() is the sum of all external force (like gravity, etc).
is the sum of all external force (like gravity, etc).
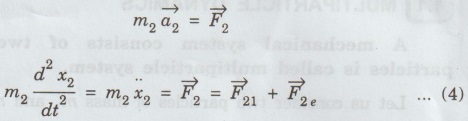
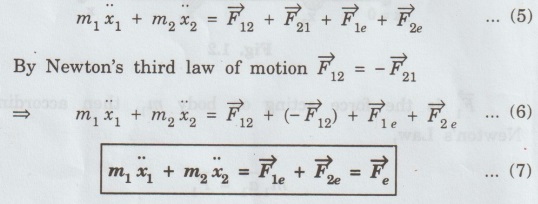
![]() is net external force on system of two particles.
is net external force on system of two particles.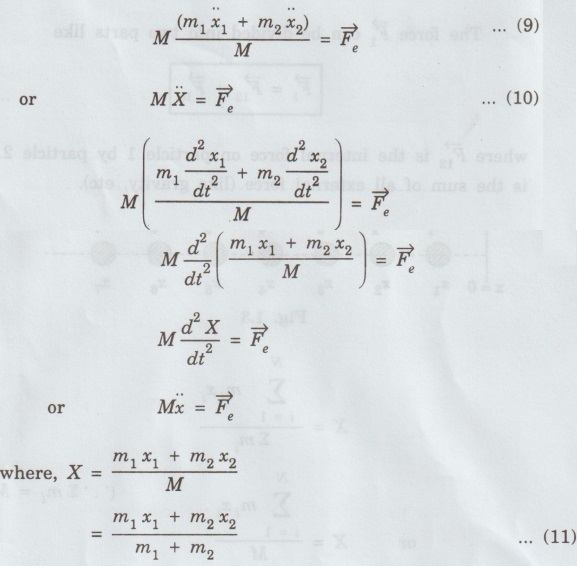
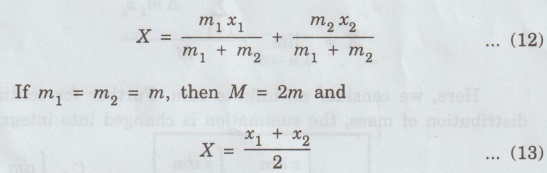
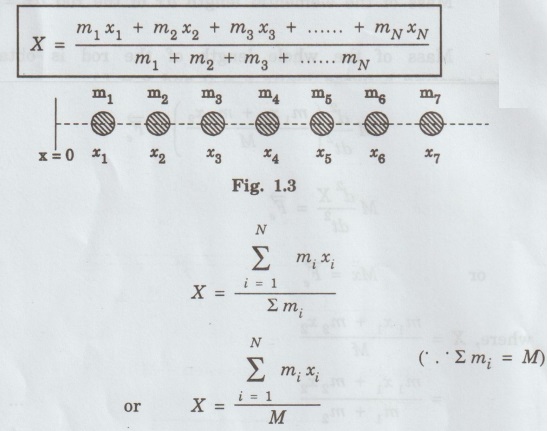
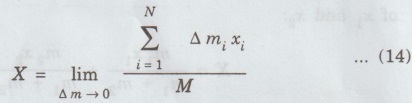
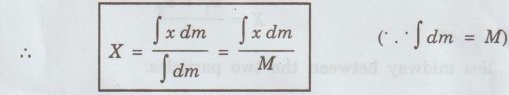
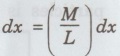
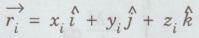 is the position vector of the particle. So the position of the CM is
is the position vector of the particle. So the position of the CM is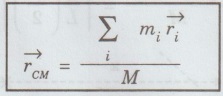
Centre of Mass : Definition
Engineering Physics: Unit I: Mechanics : Tag: : Definition, Examples, Equations - Multiparticle dynamics
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
