Theory of Machines: Unit I: Kinematics of Mechanisms
motion of a link
Kinematics of Mechanisms - Theory of Machines
Let a rigid link AB, rotate about a fixed point A with an uniform angular velocity o in the counter clockwise direction, as shown in Fig.2.3(a).
MOTION OF A LINK
• Let a rigid link
AB, rotate about a fixed point A with an uniform angular velocity o in the
counter clockwise direction, as shown in Fig.2.3(a).
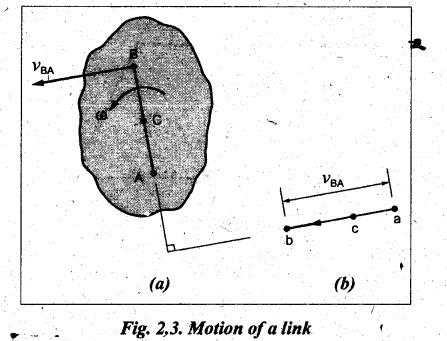
• There
is no relative motion between A and B, as the distance from A to B remains the
same. It is thus obvious that the relative motion of B with respect to A must
be perpendicular to AB.
• Therefore
velocity of any point on a link with respect to another point on the same
link is always perpendicular to the line joining these points on the
configuration diagram.
• Fig.2.3(b)
shows that the relative velocity of B with respect to A (vBA)
is perpendicular to the link AB.
Let
ω = Angular velocity of the link AB about A
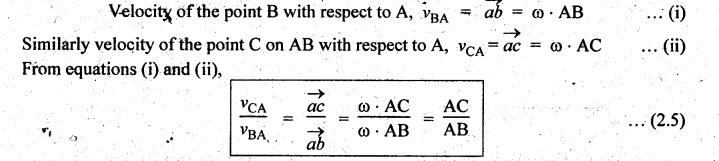
From
the equation (2.5), we can observe that the point c on ab divides
it in the same ratio as C divides the link AB.
Theory of Machines: Unit I: Kinematics of Mechanisms : Tag: : Kinematics of Mechanisms - Theory of Machines - motion of a link
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
