Engineering Physics: Unit IV: Basic Quantum Mechanics
Motion of a Free Particle
Quantum Mechanics
Let us consider electrons propagating freely in space in the positive x-direction and not acted upon by any force.
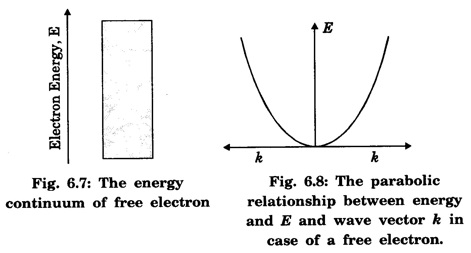
MOTION OF A FREE PARTICLE Let us consider electrons propagating freely in space in the positive x-direction and not acted upon by any force. As the electrons are not acted upon by any force, their potential energy V is zero. Schrodinger equation The general solution of the above equation is where A and B are constants. As it is assumed that the waves propagate only in the positive x-direction, we can write There are no boundary conditions to be considered and hence there are no restrictions on k. All values of the energy are allowed. The allowed energy values form a continuum and are given by A freely moving electron therefore possess a continuous energy spectrum as shown in fig. 6.7. It is noted from equation (2) that The k known as wave vector describes the wave properties of the electrons. Further, it is seen from the relation (2) that The plot of E as a function of k gives a parabola, as explained in fig. 6.8. The momentum is well defined in this case. Therefore, according to uncertainty principle it is difficult to assign a position to the electron. The uncertainty in position will be infinity which means that the electron position is indeterminate.
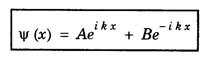
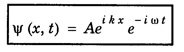

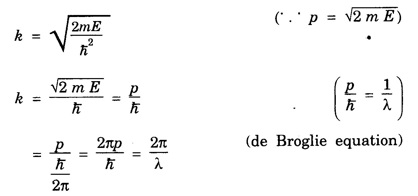
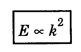
Engineering Physics: Unit IV: Basic Quantum Mechanics : Tag: : Quantum Mechanics - Motion of a Free Particle
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
